 |
Главная |
Преобразование подобия. Группа подобий.
|
из
5.00
|
Подобием пространства 
 называется преобразование f этого пространства, обладающее следующим свойством: существует число k
называется преобразование f этого пространства, обладающее следующим свойством: существует число k 
(коэффициент подобия), такое, что
 (f (Α), f (Β))=
(f (Α), f (Β))= 

Движение является частным случаем подобия ( 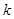 =1). Другим частным случаем подобия является гомотетия.
=1). Другим частным случаем подобия является гомотетия.
Пусть даны точка S  и число
и число 
 R,
R, 
 . Гомотетией с центром S и коэффициентом
. Гомотетией с центром S и коэффициентом  называется отображение g:
называется отображение g:  по закону
по закону
g(Μ)=Μ´ 
 =
= 
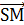 .
.
Отсюда следует, что g(S)=S (S-неподвижная точка), и если Μ  , то точка Μ´ лежит на прямой (SΜ). Возьмем произвольные точки Μ и Ν и пусть
, то точка Μ´ лежит на прямой (SΜ). Возьмем произвольные точки Μ и Ν и пусть
Μ´= g(Μ), Ν´= g(Ν).
Тогда  =
= 
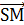 ,
,  =
= 
 =
= 
 . (1)
. (1)
Возьмем еще одну точку L на прямой ( MN). Для точки L ´=f( L ) имеем:  =
= 
 (2)
(2)
Пусть точки M и N различны. Тогда  =
= 
 , (3)
, (3)
(1),(2) 
 =
= 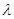
 .
. 
 (4)
(4)
(3),(4)  гомотетия сохраняет отношение трех точек прямой.Поэтому в гомотетии отрезок переходит в отрезок, луч – в луч, прямая – в прямую, полуплоскость – в полуплоскость. Если
гомотетия сохраняет отношение трех точек прямой.Поэтому в гомотетии отрезок переходит в отрезок, луч – в луч, прямая – в прямую, полуплоскость – в полуплоскость. Если  - направляющий вектор прямой
- направляющий вектор прямой  a, то
a, то  - направляющий вектор прямой a ´= f ( a ) .
- направляющий вектор прямой a ´= f ( a ) .
(1)  a ´
a ´  a .
a .
Следовательно, гомотетия  переводит прямую в параллельную ей прямую. В гомотетии угол переходит в конгруэнтный ему угол. Это утверждение очевидно, если стороны угла лежат на одной прямой. Рассмотрим угол АОВ, стороны которого не лежат на одной прямой. Обозначим через Π плоскость, в которой лежит этот угол. В гомотетии g плоскость Π перейдет в плоскость Π´
переводит прямую в параллельную ей прямую. В гомотетии угол переходит в конгруэнтный ему угол. Это утверждение очевидно, если стороны угла лежат на одной прямой. Рассмотрим угол АОВ, стороны которого не лежат на одной прямой. Обозначим через Π плоскость, в которой лежит этот угол. В гомотетии g плоскость Π перейдет в плоскость Π´  Π, луч
Π, луч 
 Π перейдет в луч
Π перейдет в луч  , а луч
, а луч  -в луч
-в луч  .
.
Если угол АОВ выпуклый, то он является пересечением полуплоскостей
 и
и  :
: 
 =
= 

 .
.
В гомотетии g эти полуплоскости перейдут соответственно в полуплоскости  и
и  и, значит, угол АОВ перейдет в угол
и, значит, угол АОВ перейдет в угол
 =
= 
 .
.
Соответствующие стороны углов АОВ и А´О´В´ одинаково направлены при 

 и противоположно направлены при
и противоположно направлены при 
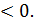 При параллельном переносе пространства на вектор
При параллельном переносе пространства на вектор  эти углы совпадают в первом случае и окажутся вертикальными во втором случае. Следовательно, эти углы конгруэнтны.
эти углы совпадают в первом случае и окажутся вертикальными во втором случае. Следовательно, эти углы конгруэнтны.
Так как g( Π )= Π ´ и g  =
= 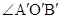 , то угол 1, дополняющий выпуклый угол АОВ до полного угла ,переходит в гомотетии g в угол 1´, дополняющий выпуклый угол Α´О´Β´ до полного угла:
, то угол 1, дополняющий выпуклый угол АОВ до полного угла ,переходит в гомотетии g в угол 1´, дополняющий выпуклый угол Α´О´Β´ до полного угла: 
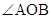
 .
.
Значит, и невыпуклый угол гомотетия переводит в конгруэнтный ему угол. Учитывая равенство (1), находим:
|  =|
=|  |
|  ,
, 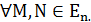
Следовательно, гомотетия является подобием. Гомотетия с центром S и коэффициентом h =-1 является центральной симметрией (относительно точки S).
Теорема. Всякое подобие является произведением гомотетии и движения.
Пусть f –подобие с коэффициентом 
 Возьмем какую-либо точку S и пусть g- гомотетия с центром S и коэффициентом
Возьмем какую-либо точку S и пусть g- гомотетия с центром S и коэффициентом  . Если M , N -произвольные точки пространства
. Если M , N -произвольные точки пространства  и Μ´=f(Μ), Ν´=f(Ν), то |
и Μ´=f(Μ), Ν´=f(Ν), то |  =
=  |
|  (5)
(5)
Пусть g(Μ)=Μ´´, g ( Ν )=Ν´´. Тогда
| 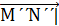 =
=  |
|  (
( 
 (6)
(6)
(5) ,(6)  |
| 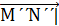 =|
=|  . (7)
. (7)
Преобразование  d = f
d = f  переводит каждую точку Μ´´ в такую точку Μ´, что имеет место равенство (7), т.е. преобразование d сохраняет расстояние между любыми двумя точками. Следовательно, d = f
переводит каждую точку Μ´´ в такую точку Μ´, что имеет место равенство (7), т.е. преобразование d сохраняет расстояние между любыми двумя точками. Следовательно, d = f  –движение. Отсюда f=d
–движение. Отсюда f=d  теорема доказана.
теорема доказана.
Следствия. 1) В подобии сохраняется отношение трех точек; следовательно, отрезок переходит в отрезок, луч в луч;
2) в подобии угол переходит в конгруэнтный ему угол;
3) в подобии  – плоскость переходит в
– плоскость переходит в  -плоскость.
-плоскость.
Пусть дано подобие с коэффициентом  Возьмем какой-либо ортонормированный репер R={О,
Возьмем какой-либо ортонормированный репер R={О,  }. По доказанному j =d
}. По доказанному j =d  , где g- гомотетия с центром О и коэффициентом k , а d-движение. Произвольная точка Μ(
, где g- гомотетия с центром О и коэффициентом k , а d-движение. Произвольная точка Μ(  ) перейдет в гомотетии g в такую точку Μ´´(
) перейдет в гомотетии g в такую точку Μ´´( 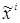 ) , что
) , что  Следовательно,
Следовательно,
 (8)
(8)
Движение d переводит точку Μ´´ в точку Μ´=d(Μ´´)=f(Μ). Если  - координата точки Μ´´, то, как известно,
- координата точки Μ´´, то, как известно,

 (9),
(9),
где ||  || - ортогональная матрица.
|| - ортогональная матрица.
(8),(9)  (10)
(10)
Так выражаются в ортонормированном репере R координаты точки Μ´=f(Μ) через координаты точки Μ в подобии f.
|
из
5.00
|
Обсуждение в статье: Преобразование подобия. Группа подобий. |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

