 |
Главная |
N -мерное евклидово пространство.
|
из
5.00
|
Пусть V - n-мерное векторное пространство над полем R вещественных чисел. Билинейной формой, определенной на векторном пространстве V, называется отображение
g:  ,
,
линейное по каждому аргументу, т.е. удовлетворяющее условию:
 и
и
 ,
,
 и
и 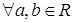 .
.
Пусть на векторном пространстве V задана билинейная форма g. Возьмем в V какой-либо базис { 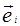 } (
} (  Для
Для 

 V имеем :
V имеем :  и, значит, g(
и, значит, g( 
Обозначим  через
через  . Тогда
. Тогда
g( 

Квадратная матрица  называется матрицей билинейной формы g в базисе
называется матрицей билинейной формы g в базисе  . Таким образом, чтобы задать билинейную форму g: V
. Таким образом, чтобы задать билинейную форму g: V 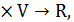 достаточно в пространстве V задать базис
достаточно в пространстве V задать базис  и взять какую-либо квадратную матрицу G c элементами
и взять какую-либо квадратную матрицу G c элементами  Тогда значение билинейной формы для
Тогда значение билинейной формы для 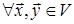 вычисляется по формуле (*).Билинейная форма называется симметрической, если
вычисляется по формуле (*).Билинейная форма называется симметрической, если  для
для  .
.
Билинейная форма g на векторном пространстве V называется вырожденной, если  .
.
Если же такого вектора  не существует, то форма g называется невырожденной.
не существует, то форма g называется невырожденной.
По формуле (  ) для вырожденной формы имеем:
) для вырожденной формы имеем:  (1)
(1)
для  Но (1) есть многочлен 1-й степени относительно
Но (1) есть многочлен 1-й степени относительно  ,
,
и он равен нулю при любых значениях переменных  . Значит, все его
. Значит, все его
коэффициенты равны нулю: 
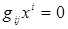 .
.
Это есть система линейных однородных уравнений с n неизвестными. Такая система имеет ненулевое решение тогда и только тогда, когда  т.е. матрица G вырожденная. Отсюда следует, что билинейная форма g ,будет невырожденной тогда и только тогда, когда её матрица G невырожденная
т.е. матрица G вырожденная. Отсюда следует, что билинейная форма g ,будет невырожденной тогда и только тогда, когда её матрица G невырожденная 
Векторное пространство V над полем R называется евклидовым векторным пространством, если на нем задана положительная билинейная форма g.
Употребляют такие названия:
Число  - скалярное произведение векторов
- скалярное произведение векторов  и
и  (его обозначают
(его обозначают
через  , или
, или  - скалярный квадрат вектора
- скалярный квадрат вектора  ;
;  - неотрицательное число - норма или длина вектора
- неотрицательное число - норма или длина вектора  .
.
Векторы  и
и 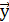 называются ортогональными, если их скалярное произведение равно нулю:
называются ортогональными, если их скалярное произведение равно нулю:  =0.
=0.  Вектор
Вектор  называется ортом (или единичным ), если
называется ортом (или единичным ), если  =1. Если
=1. Если  ,то вектор
,то вектор  =
=  является ортом. Базис {
является ортом. Базис {  } евклидова векторного пространства V называется ортонормированным, если все его векторы единичные и попарно ортогональные:
} евклидова векторного пространства V называется ортонормированным, если все его векторы единичные и попарно ортогональные:

Расстояние между двумя точками.
Угол между векторами.
1. Расстоянием ρ (А, В) между точками А, В  Еn называется длина вектора
Еn называется длина вектора  :
:
ρ (А, В) =  . (1)
. (1)
Возьмём в Еn ортонормированную систему координат или ортонормированный репер, т. е. такой аффинный репер R =  , координатные векторы
, координатные векторы  которого образуют ортонормированный базис пространства переносов V.
которого образуют ортонормированный базис пространства переносов V.
Так как теперь 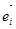 ·
· 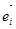 = 1,
= 1, 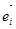 ·
·  = 0 (i ≠ j ) и, значит, gij = 1, gij = 0
= 0 (i ≠ j ) и, значит, gij = 1, gij = 0
(i ≠ j), то для любого вектора  получим:
получим:

и, следовательно,
 (2)
(2)
Так выражается длина вектора через его координаты в ортонормированном базисе.
Пусть А и В даны своими координатами в ортонормированном репере:
 . Тогда
. Тогда
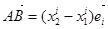 . (3)
. (3)
(1), (2), (3) 
Так вычисляется расстояние между двумя точками в ортонормированной системе координат.
Теорема. Расстояние между двумя точками в пространстве Е n удовлетворяет неравенству треугольника
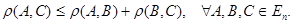
Это значит, что
 (4)
(4)
▲Как известно,  . Пусть
. Пусть 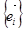 - ортонормированный базис и
- ортонормированный базис и  Тогда
Тогда  Нам надо доказать, как это следует из (4), что
Нам надо доказать, как это следует из (4), что  . Здесь каждая из сумм положительна. После возведения обеих частей неравенства в квадрат, получим:
. Здесь каждая из сумм положительна. После возведения обеих частей неравенства в квадрат, получим:

(неравенство Коши – Буняковского). Таким образом, доказательство неравенства (4) сводится к доказательству неравенству Коши – Буняковского. Докажем последнее. Ясно, что
 .
.
Следовательно, квадратный трёхчлен, стоящий слева, принимает только неотрицательное значения, поэтому его дискриминант
 , (#)
, (#)
откуда и следует неравенство Коши – Буняковского. ▲
Лемма.  (теорема Пифагора в Еn)
(теорема Пифагора в Еn)

▲ 
▲ (*)
Следствие. (*) 
Итак, 
Теорема. Если три точки А, В и С различны, то неравенство в формуле (4) имеет место тогда и только тогда, когда точка В лежит между А и
▲ А. Пусть точка В лежит между А и С,





т. е.  Тогда (в обозначениях предыдущей теоремы)
Тогда (в обозначениях предыдущей теоремы)
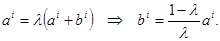
Вычислим левую часть формулы (#):

Значит, в этом случае в формуле (4) имеем знак равенства.
Б. Пусть точка В не лежит на прямой (АС):

Найдём на прямой (АС) точку D ( 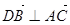 (такая точка называется ортогональной проекцией точки В на прямую (АС)). Ищем
(такая точка называется ортогональной проекцией точки В на прямую (АС)). Ищем  , т. е.
, т. е.

и точка D определена. По следствию из леммы:

Отсюда следует, что если точка В не лежит на прямой (АС), то сумма расстояний  не может быть наименьшей. Значит, равенство в формуле (4) возможно только в случае, когда точка В лежит на прямой (АС). Пусть точка В лежит на прямой (АС) и отлична от точек А и С. Тогда
не может быть наименьшей. Значит, равенство в формуле (4) возможно только в случае, когда точка В лежит на прямой (АС). Пусть точка В лежит на прямой (АС) и отлична от точек А и С. Тогда  Возможны три случая: 1)
Возможны три случая: 1)  (точка В лежит между А и С); 2)
(точка В лежит между А и С); 2) 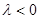 ; 3)
; 3)  .
.
Докажем, что если
 (4')
(4')
то случаи 2 и 3 не могут иметь места.
В случае 2:
 (5)
(5)
Но

(5)  , и так как
, и так как 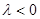 , то
, то 
Следовательно, точка А лежит между В и С и по доказанному в п0 А: 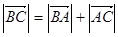

|
|
|
что противоречит условию (4').
В случае 3: 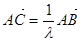 , где
, где  , и, значит, точка С лежит между А и В. По доказанному в п0 А:
, и, значит, точка С лежит между А и В. По доказанному в п0 А: 
 |
|
|
|
что противоречит условию (4').
Итак, если имеет место равенство (4'), то точка В лежит между А и С. ▲
Следствие. Из трёх различных точек А, В и С одной прямой всегда одна и только одна лежит между двумя другими.
2. Возьмём ненулевые векторы  и какую-либо точку О. По первой аксиоме Вейля
и какую-либо точку О. По первой аксиоме Вейля  .
. 
Выпуклый угол АОВ называется углом между данными векторами 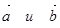 . Пусть
. Пусть  - орты векторов
- орты векторов  соответственно. Тогда
соответственно. Тогда

Найдём вектор  , такой, чтобы вектор
, такой, чтобы вектор  был ортогонален вектору
был ортогонален вектору  :
:

Так как в пространстве Е n скалярный квадрат любого вектора неотрицателен, то 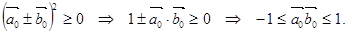
Следовательно, в числовом промежутке  существует число α, такое, что
существует число α, такое, что  . Это число α называется величиной угла между векторами
. Это число α называется величиной угла между векторами  и обозначается обычно через
и обозначается обычно через  . Учитывая, что
. Учитывая, что
 ,
,
находим
 (**)
(**)
Пример. В евклидовом пространстве Е4 дан треугольник АВС с координатами вершин А (1, -1, 2, 3), В (0, 1, -1, 1), С(2, 0, 1, -2) в ортонормированном репере. Вычислить внутренний угол треугольника при вершине А.
Находим:
а)  ;
;
б) и по формуле (**)

|
из
5.00
|
Обсуждение в статье: N -мерное евклидово пространство. |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

