 |
Главная |
Движения евклидова пространства.
|
из
5.00
|
1.Возьмём в пространстве Еn упорядоченную пару ортонормированных реперов 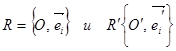 и каждой точке
и каждой точке 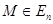 , имеющей координаты xi в репере R, поставим в соответствие точку М' с теми же координатами xi относительно репера R'. Мы получим преобразование пространства Еn, которое называется движением (или перемещением, или изометрией).
, имеющей координаты xi в репере R, поставим в соответствие точку М' с теми же координатами xi относительно репера R'. Мы получим преобразование пространства Еn, которое называется движением (или перемещением, или изометрией).
Таким образом, движение является частным случаем аффинного преобразования аффинного пространства An, из которого получено евклидово Еn, а именно: движение – это такое аффинное преобразование, которое переводит ортонормированный репер в ортонормированный.
Движение пространства Еn порождается (при заданной паре соответствующих точек О и О') таким линейным преобразованием пространства переносов V, которое переводит ортонормированный базис 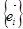 в ортонормированный
в ортонормированный 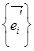 . Такое линейное преобразование евклидового векторного пространства V называют ортогональным (оно сохраняет скалярное произведение векторов). Следовательно, движение пространства Еn порождается ортогональным преобразованием пространства переносов V.
. Такое линейное преобразование евклидового векторного пространства V называют ортогональным (оно сохраняет скалярное произведение векторов). Следовательно, движение пространства Еn порождается ортогональным преобразованием пространства переносов V.
Так как движение – частный случай аффинного преобразования, то всякое движение: 1) сохраняет отношение трёх точек; 2) переводит отрезок в отрезок, луч в луч, k-плоскость в k-плоскость.
В частности, движение переводит прямую в прямую с сохранением порядка точек на прямой.
Пусть движение f пространства Еn порождено ортогональным преобразованием 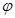 пространства переносов V. Возьмём в Еn две произвольные точки M и N и пусть f(M) = M', f(N) = N'. Тогда
пространства переносов V. Возьмём в Еn две произвольные точки M и N и пусть f(M) = M', f(N) = N'. Тогда 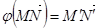 . А так как
. А так как 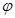 - ортогональное преобразование пространства V и, значит, сохраняет длину вектора, то
- ортогональное преобразование пространства V и, значит, сохраняет длину вектора, то
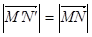 .
.
Следовательно, движение пространства Еn сохраняет расстояние между двумя точками этого пространства.
Справедливо и обратное утверждение:
Теорема. Если преобразование f евклидова пространства Е n сохраняет расстояние между двумя точками, то f – движение.
▲Возьмём три произвольные точки О, А, В. Тогда
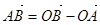 ,
,
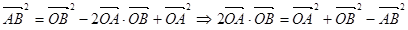 . (1)
. (1)
Пусть преобразование f переводит точки О, А, В в точки О', А', В' соответственно. Тогда можно написать равенство, аналогичное равенству (1):
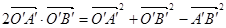 . (2)
. (2)
По условию теоремы правые части равенств (1) и (2) равны; следовательно, равны и левые части. Отсюда
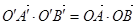 . (3)
. (3)
Пусть 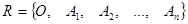 - ортонормированный репер в Еn и, значит, векторы
- ортонормированный репер в Еn и, значит, векторы 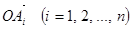 единичные, попарно ортогональные. Если
единичные, попарно ортогональные. Если
f (O) = O', f (Ai) = Ai', то в силу формулы (3) векторы 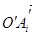 тоже единичные, попарно ортогональные и, следовательно, репер
тоже единичные, попарно ортогональные и, следовательно, репер 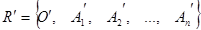 ортонормированный. Возьмём произвольную точку
ортонормированный. Возьмём произвольную точку 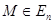 , и пусть f (M) = M'. Обозначим через xi координаты точки М в репере R, а через yi – координаты точки М' в репере R'. Тогда
, и пусть f (M) = M'. Обозначим через xi координаты точки М в репере R, а через yi – координаты точки М' в репере R'. Тогда
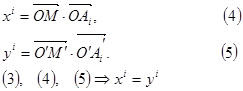
и, следовательно, преобразование f есть движение. ▲
2. Пусть V – евклидово векторное пространство размерности n. Линейное преобразование 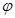 пространства V называется ортогональным, если оно переводит ортонормированный базис
пространства V называется ортогональным, если оно переводит ортонормированный базис 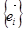 в ортонормированный базис
в ортонормированный базис 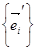 или, что равносильно этому, если оно сохраняет скалярное произведение векторов.
или, что равносильно этому, если оно сохраняет скалярное произведение векторов.
Пусть 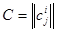 - матрица перехода от базиса
- матрица перехода от базиса 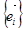 к базису
к базису 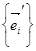 :
:
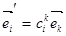 .
.
Тогда
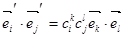 .
.
Учитывая, что базисы 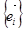 и
и 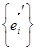 ортонормированные, находим:
ортонормированные, находим:
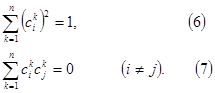
Таким образом, матрица С обладает следующим свойством: сумма квадратов элементов каждого столбца равна единице, а сумма произведений соответствующих элементов двух различных столбцов равна нулю.
Квадратная матрица, обладающая этим свойством, называется ортогональной.
Заметим, что если базис 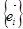 задан, то матрица С определяет линейное преобразование
задан, то матрица С определяет линейное преобразование 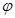 (так как она определяет базис
(так как она определяет базис 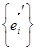 ). Поэтому можно высказать следующее утверждение6 в ортонормированном базисе
). Поэтому можно высказать следующее утверждение6 в ортонормированном базисе 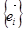 всякое ортогональное преобразование
всякое ортогональное преобразование 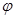 определяется с помощью ортогональной матрицы С.
определяется с помощью ортогональной матрицы С.
Обратно, пусть 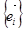 - ортонормированный базис евклидова векторного пространства размерности n. Возьмём какую-либо ортогональную n
- ортонормированный базис евклидова векторного пространства размерности n. Возьмём какую-либо ортогональную n  n матрицу
n матрицу 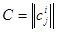 и рассмотрим векторы
и рассмотрим векторы 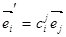 . Равенства (6) и (7) показывают, что векторы
. Равенства (6) и (7) показывают, что векторы 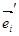 единичные и попарно ортогональные и, значит, образуют ортонормированный базис
единичные и попарно ортогональные и, значит, образуют ортонормированный базис 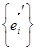 . Следовательно, линейное преобразование пространства V, переводящее базис
. Следовательно, линейное преобразование пространства V, переводящее базис 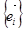 в базис
в базис 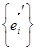 , является ортогональным. Иначе говоря, если линейное преобразование
, является ортогональным. Иначе говоря, если линейное преобразование 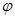 евклидова векторного пространства задаётся в каком-либо ортонормированном базисе при помощи ортогональной матрицы, то преобразование
евклидова векторного пространства задаётся в каком-либо ортонормированном базисе при помощи ортогональной матрицы, то преобразование  ортогональное.
ортогональное.
Нетрудно заметить, что равенства (6) и (7) равносильны одному матричному равенству:
С'С = Е (8)
(где Е – единичная матрица), или, что то же самое, равенству:
С' = С-1.
Следовательно, матрица С ортогональная тогда и только тогда, когда транспонированная матрица С' равна обратной матрице С-1.
(8)  (С')' = (С')-1;
(С')' = (С')-1;
значит, если матрица С ортогональная, то и транспонированная матрица С' ортогональна.
Далее имеем:
(8) 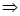 det (C') * det (C) = 1. (9)
det (C') * det (C) = 1. (9)
Как известно из алгебры, det (C') = det (C), и равенство (9) принимает вид:
(det (C))2 = 1 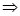 det (C) =
det (C) = 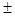 1,
1,
Определитель ортогональной матрицы равен 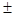 1.
1.
3. Пусть движение f пространства En задано упорядоченной парой ортонормированных реперов 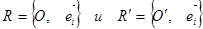 . Так как движение f – частный случай аффинного преобразования, то координаты yi точки М' = f(М) относительно репера R выражаются через координаты xi точки М относительно того же репера по формулам вида:
. Так как движение f – частный случай аффинного преобразования, то координаты yi точки М' = f(М) относительно репера R выражаются через координаты xi точки М относительно того же репера по формулам вида:
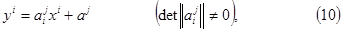
что можно записать в матричной форме одним равенством:
y = Ax + a. (11)
Так как f – движение, то оно порождается некоторым ортогональным преобразованием 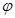 пространства переносов V. В формулах (10), (11) матрица
пространства переносов V. В формулах (10), (11) матрица 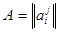 - матрица этого преобразования
- матрица этого преобразования 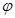 в базисе
в базисе 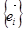 и, следовательно, А – ортогональная матрица.
и, следовательно, А – ортогональная матрица.
Обратно, пусть в Еn задан ортонормированный репер 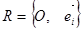 . Напишем формулы (10), в которых матрица
. Напишем формулы (10), в которых матрица 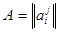 ортогональная. Преобразование f пространства Еn, определяемое этими формулами, является аффинным. Оно порождается таким линейным преобразованием
ортогональная. Преобразование f пространства Еn, определяемое этими формулами, является аффинным. Оно порождается таким линейным преобразованием 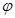 пространства переносов V, которое в ортонормированном базисе
пространства переносов V, которое в ортонормированном базисе 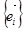 задаётся ортогональной матрицей А. следовательно,
задаётся ортогональной матрицей А. следовательно, 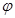 - ортогональное преобразование, а f – движение.
- ортогональное преобразование, а f – движение.
Итак, если в пространстве Еn задан ортонормированный репер R, то формулы (10) определяют движение этого пространства тогда и только тогда, когда матрица 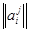 ортогональная.
ортогональная.
Ортогональное преобразование 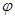 векторного пространства V переводит любой ортонормированный базис
векторного пространства V переводит любой ортонормированный базис 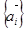 в базис
в базис 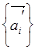 также ортонормированный. Следовательно, движение f пространства Еn переводит любой ортонормированный репер
также ортонормированный. Следовательно, движение f пространства Еn переводит любой ортонормированный репер 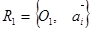 в репер
в репер 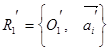 также ортонормированный. Поэтому движение f можно определить заданием любой пары соответствующих ортонормированных реперов: R, R' или R1, R1'.
также ортонормированный. Поэтому движение f можно определить заданием любой пары соответствующих ортонормированных реперов: R, R' или R1, R1'.
Группа движений пространства  .
.
Обозначим через  , множество всех движений евклидова пространства
, множество всех движений евклидова пространства  . Всякое движение f пространства
. Всякое движение f пространства 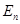 является таким преобразованием этого пространства, которое сохраняет расстояние между любыми двумя точками. Следовательно, произведение gf двух движений f и g, а также обратное преобразование f -1 будут преобразованиями пространства
является таким преобразованием этого пространства, которое сохраняет расстояние между любыми двумя точками. Следовательно, произведение gf двух движений f и g, а также обратное преобразование f -1 будут преобразованиями пространства 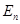 , сохраняющими расстояние между любыми двумя точками, т.е. будут движениями. Следовательно, множество
, сохраняющими расстояние между любыми двумя точками, т.е. будут движениями. Следовательно, множество  является группой (относительно умножения), она называется группой движений пространства
является группой (относительно умножения), она называется группой движений пространства 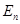 .
.
Две фигуры 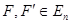 называются конгруэнтными, если они эквивалентны относительно группы
называются конгруэнтными, если они эквивалентны относительно группы 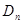 , т.е. если существует движение, которое переводит одну из этих фигур в другую.
, т.е. если существует движение, которое переводит одну из этих фигур в другую.
Движение f называется движением первого (второго) рода, если в формулах: 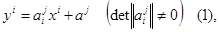 задающих это движение в ортонормированном репере
задающих это движение в ортонормированном репере 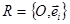 , имеет место соотношение
, имеет место соотношение 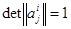 (соответственно
(соответственно 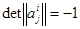 ).
).
Следовательно, движение 1-го рода сохраняет ориентацию пространства (т.е. переводит репер 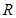 в репер
в репер 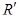 , одинаково с ним ориентированный), а движение 2-го рода меняет ориентацию пространства (переводит репер
, одинаково с ним ориентированный), а движение 2-го рода меняет ориентацию пространства (переводит репер 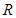 в противоположно ориентированный репер
в противоположно ориентированный репер 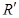 ).
).
Отметим важнейшие подгруппы группы движений.
I. Множество всех движений 1-го рода является группой (группа движений 1-го рода); движения 1-го рода сохраняют ориентацию каждого репера.
II. Множество движений 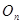 всех движений, оставляющих неподвижной точку
всех движений, оставляющих неподвижной точку 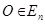 , также является группой. В ортонормированном репере
, также является группой. В ортонормированном репере 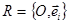 всякое движение
всякое движение 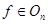 определяется формулами (1), где
определяется формулами (1), где 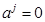 , тогда
, тогда 
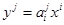 (*) или в матричной форме:
(*) или в матричной форме: 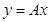 (**), где
(**), где 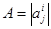 - матрица (в базисе
- матрица (в базисе 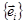 ) того ортогонального преобразования φ пространства переносов V , которое порождает данное движение f . Как известно, принимая точку О за начало пространства
) того ортогонального преобразования φ пространства переносов V , которое порождает данное движение f . Как известно, принимая точку О за начало пространства 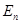 с векторным пространством φ. Тогда рассматриваемоедвижение f пространства
с векторным пространством φ. Тогда рассматриваемоедвижение f пространства 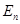 будет просто совпадать с порождающим его ортогональным преобразованием φ векторного пространства V .
будет просто совпадать с порождающим его ортогональным преобразованием φ векторного пространства V .
Учитывая это, всякое движение 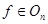 называется ортогональным преобразованием пространства
называется ортогональным преобразованием пространства  , а группу
, а группу 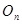 - группой ортогональных преобразований, этого пространства (или ортогональной группой).
- группой ортогональных преобразований, этого пространства (или ортогональной группой).
Расстояние 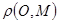 точки М от начала О является инвариантом относительно группы
точки М от начала О является инвариантом относительно группы 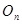 .
.
ІІІ. Ортогональные преобразования 1-го рода ( в формулах (*) 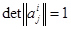 ) называются вращениями пространства
) называются вращениями пространства  вокруг точки О. Множество
вокруг точки О. Множество  всех вращений пространства вокруг точки О, является группой (группа вращений пространства
всех вращений пространства вокруг точки О, является группой (группа вращений пространства  ). Она является подгруппой группы
). Она является подгруппой группы 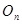 , также подгруппой группы движений 1-го рода.
, также подгруппой группы движений 1-го рода.
Расстояние 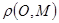 и ориентация репера сохраняются при любых вращениях вокруг точки О.
и ориентация репера сохраняются при любых вращениях вокруг точки О.
IV. Если в формулах (1), задающих движение, матрица 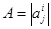 единичная, то эти формулы примут вид:
единичная, то эти формулы примут вид: 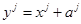 .
.
Такое движение называется параллельным переносом и вполне определяется вектором переноса 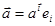 . Следовательно, и в евклидовом пространстве
. Следовательно, и в евклидовом пространстве  (как и в аффинном
(как и в аффинном  ) мы имеем группу переносов. Параллельные переносы сохраняют любое направление в
) мы имеем группу переносов. Параллельные переносы сохраняют любое направление в  (т.е. переводят в себя каждое множество одинаково направленных лучей). Очевидно, перенос пространства
(т.е. переводят в себя каждое множество одинаково направленных лучей). Очевидно, перенос пространства 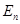 - движение 1-го рода.
- движение 1-го рода.
Рассмотрим, движения трехмерного евклидова пространства 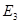 .
.
а) Пусть дана плоскость 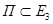 . Две точки
. Две точки 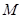 и
и 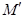 называются симметричными относительно плоскости
называются симметричными относительно плоскости 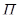 , если плоскость
, если плоскость 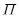 перпендикулярна отрезку
перпендикулярна отрезку 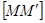 и проходит через его середину. Если же
и проходит через его середину. Если же 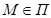 , то говорят, что эта точка симметрична самой себе относительно
, то говорят, что эта точка симметрична самой себе относительно 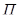 .
.
Отображение f: 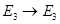 называется симметрией относительно плоскости
называется симметрией относительно плоскости 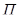 (или отражением от плоскости
(или отражением от плоскости 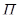 ), если точки
), если точки 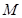 и
и 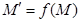 симметричны относительно плоскости
симметричны относительно плоскости 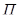 ,
, 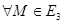 .
.
Рассмотрим такое отображение f и примем плоскость 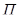 в качестве плоскости
в качестве плоскости 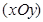 ортонормированной системы координат
ортонормированной системы координат 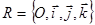 . Если
. Если 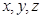 - координаты точки
- координаты точки  в репере
в репере  , то точка
, то точка 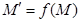 имеет координаты
имеет координаты 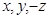 в том же репере. Возьмем еще какие- либо две точки
в том же репере. Возьмем еще какие- либо две точки 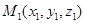 и
и 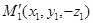 симметричные относительно плоскости
симметричные относительно плоскости 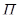 . Тогда, как легко подсчитать,
. Тогда, как легко подсчитать, 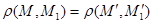 . Отсюда следует, что f-движение.
. Отсюда следует, что f-движение.
Как известно, репер 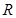 можно определить упорядоченной четверкой точек
можно определить упорядоченной четверкой точек 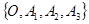 .
.
В симметрии относительно плоскости 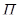 точки
точки 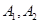 инвариантны, а точка
инвариантны, а точка 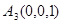 перейдет в точку
перейдет в точку 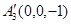 . Следовательно, f переводит репер
. Следовательно, f переводит репер 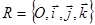 в репер
в репер 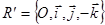 . Здесь определитель матрицы С перехода от базиса
. Здесь определитель матрицы С перехода от базиса 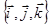 к базису
к базису 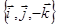
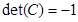 , и поэтому симметрия относительно плоскости есть движение II рода;
, и поэтому симметрия относительно плоскости есть движение II рода;
б) рассмотрим пару одинаково ориентированных ортонормированных реперов 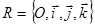 и
и 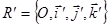 .
.
Существует движение, которое переводит репер 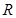 в
в 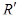 . Это движение называется поворотом пространства вокруг оси
. Это движение называется поворотом пространства вокруг оси 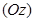 на угол
на угол 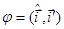 .
.
Так как реперы 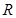 и
и 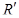 одинаково ориентированы, то поворот –движение I рода. Ясно, что любая точка оси поворота инвариантна в этом повороте.
одинаково ориентированы, то поворот –движение I рода. Ясно, что любая точка оси поворота инвариантна в этом повороте.
Угол поворота φ считают ориентированным, если 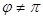 . Именно, угол φ ориентирован положительно (отрицательно), если тройка векторов
. Именно, угол φ ориентирован положительно (отрицательно), если тройка векторов 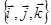 ориентирована положительно (отрицательно). Если угол поворота
ориентирована положительно (отрицательно). Если угол поворота 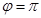 , то каждая точка М переходит в симметричную ей относительно прямой
, то каждая точка М переходит в симметричную ей относительно прямой 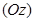 точку
точку 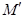 . Это значит, что если
. Это значит, что если 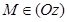 , то
, то 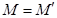 , если же
, если же 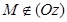 , то прямая
, то прямая 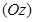 перпендикулярна к отрезку
перпендикулярна к отрезку 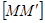 и делит его пополам. Такое движение пространства называется симметрией относительно прямой
и делит его пополам. Такое движение пространства называется симметрией относительно прямой 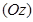 ,(это частный случай поворота, когда угол поворота
,(это частный случай поворота, когда угол поворота 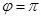 );
);
в) произведение поворота на перенос, вектор которого параллелен оси поворота, называется винтовым движением. Поворот и перенос- движение I рода;
г) произведение поворота на отражение от плоскости 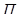 , перпендикулярной оси поворота, называется поворотным отражением. Очевидно, это движение II рода. Ось s поворота, угол φ, плоскость
, перпендикулярной оси поворота, называется поворотным отражением. Очевидно, это движение II рода. Ось s поворота, угол φ, плоскость 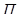 и точка
и точка 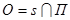 называются соответственно осью, углом, плоскостью, и центром поворотного отражения.
называются соответственно осью, углом, плоскостью, и центром поворотного отражения.
Рассмотрим частный случай поворотного отражения, когда 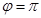 . Легко заметить, что в этом движении каждая точка
. Легко заметить, что в этом движении каждая точка 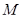 переходит в симметричную ей относительно точки О точку
переходит в симметричную ей относительно точки О точку 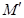 . Движение пространства, обладающее этим свойством, называется центральной симметрией (или отражением точки).
. Движение пространства, обладающее этим свойством, называется центральной симметрией (или отражением точки).
Теорема. Пусть 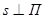 и
и 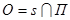 . Произведение поворота на угол φ вокруг оси
. Произведение поворота на угол φ вокруг оси 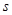 на отражение от точки О есть поворотное отражение на угол
на отражение от точки О есть поворотное отражение на угол 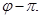 Осью, плоскостью и центром этого поворотного отражения служат соответственно
Осью, плоскостью и центром этого поворотного отражения служат соответственно 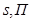 и О.
и О.
Пусть 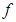 -поворот вокруг оси
-поворот вокруг оси 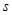 на угол
на угол 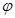 , g-отражение от точки О,
, g-отражение от точки О, 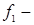 поворот вокруг оси
поворот вокруг оси 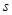 на угол
на угол 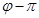 ,
, 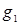 - симметрия относительно плоскости П. Для произвольной точки M пространства находим :
- симметрия относительно плоскости П. Для произвольной точки M пространства находим : 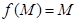 ´,
´, 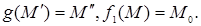 Так как
Так как 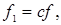 где
где 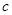 - симметрия относительно прямой
- симметрия относительно прямой 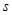 , то точки
, то точки  ,
, 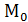 симметричны относительно оси
симметричны относительно оси 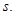 Следовательно, точки
Следовательно, точки 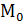 и
и 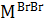 симметричны относительно плоскости П:
симметричны относительно плоскости П: 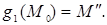
Итак, 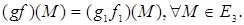 Поэтому
Поэтому 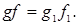 Но
Но 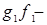 поворотное отражение (с осью
поворотное отражение (с осью 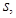 плоскостью П и центром О) на угол
плоскостью П и центром О) на угол 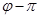 .
.
|
из
5.00
|
Обсуждение в статье: Движения евклидова пространства. |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

