 |
Главная |
Квадрики в евклидовом n – пространстве.
|
из
5.00
|
1.Пусть в евклидовом пространстве Еn дана квадрика Q, определённая в некотором ортонормированном репере  уравнением:
уравнением:
 (1)
(1)
Совокупность старших членов  определяет квадратичную форму на пространстве переносов V. Мы можем перейти к такому ортонормированному базису
определяет квадратичную форму на пространстве переносов V. Мы можем перейти к такому ортонормированному базису 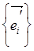 , в котором квадратичная форма
, в котором квадратичная форма 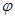 имеет канонический вид:
имеет канонический вид:
 ,
,
Где r – ранг формы  - характеристические корни её матрицы
- характеристические корни её матрицы  . Следовательно, в репере
. Следовательно, в репере  квадрика Q будет иметь уравнение:
квадрика Q будет иметь уравнение:
 . (2)
. (2)
Поступая далее, как и в случае квадрики в аффинном пространстве, мы получим те же канонические уравнения квадрик, но не получим (вообще говоря) их нормальных уравнений, так как необходимая для этого замена координатных векторов  при
при  здесь невозможна (векторы нового репера должны быть единичными) следовательно, в теории квадрик в евклидовом пространстве Еn основную роль играют канонические уравнения этих квадрик.
здесь невозможна (векторы нового репера должны быть единичными) следовательно, в теории квадрик в евклидовом пространстве Еn основную роль играют канонические уравнения этих квадрик.
Пусть квадрика Q1 определяется в ортонормированном репере R1 каноническим уравнением:
f (x1, x2, …, xn) = 0, (*)
а квадрика Q2 имеет в ортонормированном репере R2 каноническое уравнение:
g (x1, x2, …, xn) = 0. (**)
Легко видеть, что квадрики Q1 и Q2 конгруэнтны тогда и только тогда, когда существует такая подстановка букв x1, x2, …, xn, которая переводит уравнение (*) в уравнение (**). Так на плоскости Е2 гиперболы  конгруэнтны.
конгруэнтны.
2. Рассмотрим квадрики в трёхмерном евклидовом пространстве Е3. В аффинном пространстве А3 их существует 17 видов. Подходящим выбором ортонормированного репера в пространстве Е3 мы приведём уравнение квадрики  к одному из этих 17 видов. В полученных уравнениях коэффициенты положительны. Положив
к одному из этих 17 видов. В полученных уравнениях коэффициенты положительны. Положив
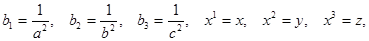
мы запишем эти уравнения так:
1)  (эллипсоид);
(эллипсоид);
2)  (мнимый эллипсоид);
(мнимый эллипсоид);
3)  (однополостный гиперболоид);
(однополостный гиперболоид);
4)  (двуполостный гиперболоид);
(двуполостный гиперболоид);
5)  (точка);
(точка);
6)  (конус с вершиной в точке О);
(конус с вершиной в точке О);
7)  (эллиптический цилиндр);
(эллиптический цилиндр);
8)  (мнимый цилиндр);
(мнимый цилиндр);
9)  (гиперболический цилиндр);
(гиперболический цилиндр);
10)  (прямая);
(прямая);
11)  (пара пересекающихся плоскостей);
(пара пересекающихся плоскостей);
12)  (пара параллельных плоскостей);
(пара параллельных плоскостей);
13)  (пара мнимых параллельных плоскостей);
(пара мнимых параллельных плоскостей);
14)  (пара совпавших плоскостей);
(пара совпавших плоскостей);
15)  (эллиптический параболоид);
(эллиптический параболоид);
16)  (гиперболический параболоид);
(гиперболический параболоид);
17) 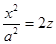 (параболический цилиндр).
(параболический цилиндр).
Задачи.
№1.
В пространстве R4 заданы две плоскости размерности два общими уравнениями:


Выяснить их взаимное расположение?
Решение : Основная и расширенная матрицы системы  , состоящей из всех четырёх уравнений, имеют вид:
, состоящей из всех четырёх уравнений, имеют вид:


Ранги этих матриц равны четырём, поэтому плоскости пересекаются в точке. Этой точкой будет начало координат.
№2.
Выяснить взаимное расположение прямой  и гиперплоскости
и гиперплоскости  пространства
пространства 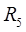 :
:

 .
.
Решение : Прямая  имеет направляющий вектор р{1, 2, 4, 0, -3}. Из теоремы *(Для того чтобы вектор р, заданный своими координатами {p1, p2, ..., pn}, принадлежал плоскости, заданной общими уравнениями
имеет направляющий вектор р{1, 2, 4, 0, -3}. Из теоремы *(Для того чтобы вектор р, заданный своими координатами {p1, p2, ..., pn}, принадлежал плоскости, заданной общими уравнениями

необходимо и достаточно, чтобы координаты вектора  удовлетворяли соотношениям:
удовлетворяли соотношениям:

Þчто р Î W 4,здесь W 4 – подпространство плоскости  таким образом Wσ совпадает с W 4. Так как начальная точка прямой (0, 0, -1, -2, 2) не лежит в плоскости
таким образом Wσ совпадает с W 4. Так как начальная точка прямой (0, 0, -1, -2, 2) не лежит в плоскости 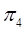 , то согласно следствию 2о (Плоскости
, то согласно следствию 2о (Плоскости  и
и 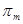 пересекаются по некоторой плоскости
пересекаются по некоторой плоскости  , где к>s >0 (0<J<1).
, где к>s >0 (0<J<1).  и
и  не пересекаются. В силу условия р Î W 4 они полностью параллельны.
не пересекаются. В силу условия р Î W 4 они полностью параллельны.
№3.
В ортонормированном базисе q 1 , q 2 ,..., qn заданы векторы:
a{a1, a2, ..., an} и b {b1, b2,..., bn}. Вычислить их скалярное произведение.
Решение : По определению координат векторов имеем:
a=a1g1+a2g2+...+angn
b=b1g1+b2g2+...+bngn.
Используя распределительный закон скалярного произведения, а также принимая во внимание, что базис g 1 ,..., gn ортонормированный, получаем:
ab=(a1g1+a2g2+...+angn)(b1g1+b2g2+...+bngn)=a1b1+a2b2+...+anbn. Таким образом, мы пришли к следующей формуле:
ab = a 1 b 1 + a 2 b 2 +...+ anbn. (1)
№4.
В ортонормированном базисе даны два ненулевых вектора a { a 1 , a 2 , ..., an } и b { b 1 , b 2 ,..., bn }. Найти косинус угла образованного данными векторами.
Решение : Пользуясь формулами: ab = a 1 b 1 + a 2 b 2 +...+ anbn и  (2), выразим ab,
(2), выразим ab,  и
и  через координаты векторов
через координаты векторов  и
и  . Подставив эти выражения в соотношение:
. Подставив эти выражения в соотношение:  получим:
получим: 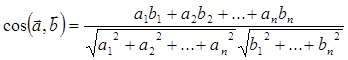 (3)
(3)
№5.
Пусть в ПДСК Оgi даны две точки со своими координатами А(х1,…, х n) и В(у1,…, у n). Вычислить расстояние между этими точками.
Решение : По определению АВ=  . Прежде всего, вычислим координаты вектора
. Прежде всего, вычислим координаты вектора  . Так как координаты точек А и В совпадают с координатами их радиус-векторов, то из соотношения
. Так как координаты точек А и В совпадают с координатами их радиус-векторов, то из соотношения  в силу теоремы (
в силу теоремы (  ) получаем:
) получаем: 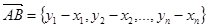 . Теперь легко вычислить длину вектора
. Теперь легко вычислить длину вектора  применяя формулу (2):
применяя формулу (2):  (4)
(4)
№6.
В ПДСК задана гиперплоскость  уравнением: a 1 х1+ a 2 х2+...+ an х n +ао=0 и точка Мо (х01,х02,…,х0 n ). Вычислить расстояние d от точки Мо до
уравнением: a 1 х1+ a 2 х2+...+ an х n +ао=0 и точка Мо (х01,х02,…,х0 n ). Вычислить расстояние d от точки Мо до  .
.
Решение : Обозначим через Nj проекцию точки Мо на 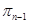 . Из теоремы *Þ a { a 1 , a 2 , ..., an } ортогонален каждому вектору гиперплоскости
. Из теоремы *Þ a { a 1 , a 2 , ..., an } ортогонален каждому вектору гиперплоскости 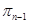 , поэтому он коллинеарен
, поэтому он коллинеарен 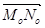 . Отсюда:
. Отсюда:  , поэтому:
, поэтому:

Записав это соотношение в координатах, и учитывая, что N0 принадлежит плоскости  , после элементарных преобразований, получили:
, после элементарных преобразований, получили:
 (5)
(5)
№7
В системе координат  даны две точки М(хi) и N(yi). Найти координаты вектора
даны две точки М(хi) и N(yi). Найти координаты вектора  .
.
Решение : По аксиоме треугольника 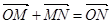 . Отсюда получаем:
. Отсюда получаем:  . Векторы
. Векторы  и
и  являются радиус-векторами точек M и N, поэтому их координаты нам известны:
являются радиус-векторами точек M и N, поэтому их координаты нам известны:  . Вектор
. Вектор  имеет координаты:
имеет координаты:  (у1-х1, у2-х2, …, уn-xn).
(у1-х1, у2-х2, …, уn-xn).
№8.
Написать уравнения 2-плоскости  пространства А4, проходящей через точку Мо(0, 1, -2, 5) и имеющей направляющее подпространство L2, заданное системой уравнений
пространства А4, проходящей через точку Мо(0, 1, -2, 5) и имеющей направляющее подпространство L2, заданное системой уравнений 
Решение : Уравнения:

в данном случае принимают вид:

Подставив значения координат точки Мо, после элементарных преобразований получим:

№9.
Написать параметрические уравнения прямой d, проходящей через точку
Мо(1, 3, 0, 0,  ) и параллельно вектору
) и параллельно вектору  в пространстве А5.
в пространстве А5.
Решение : Вектор  является базисом направляющего подпространства прямой a, поэтому уравнения в данном случае имеют вид:
является базисом направляющего подпространства прямой a, поэтому уравнения в данном случае имеют вид: 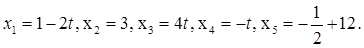
№10.
В каждом из следующих случаев выяснить взаимное расположение двух гиперплоскостей, заданных в А4 уравнениями:


Решение : а) В данном случае  и
и  , поэтому гиперплоскости пересекаются по двумерной плоскости, которая задаётся уравнениями:
, поэтому гиперплоскости пересекаются по двумерной плоскости, которая задаётся уравнениями:

б) Вычислением находим, что 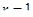 и
и  , поэтому гиперплоскости параллельны.
, поэтому гиперплоскости параллельны.
№11.
Вычислить координаты ортогональной проекции М1 точки М на гиперплоскость  :
:
1) М(1, 1, 1, -1),  :
: 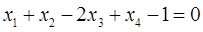
2) М(0, -1, 2, 1),  :
:  .
.
Решение : М1 проекция точки М на гиперплоскости  . Из теоремы Þ а{ a 1 , a 2 , a 3 , a 4 } ортогонален каждому вектору гиперплоскости
. Из теоремы Þ а{ a 1 , a 2 , a 3 , a 4 } ортогонален каждому вектору гиперплоскости  , поэтому он коллинеарен вектору
, поэтому он коллинеарен вектору  :
:  расстояние
расстояние  . Записав это соотношение в координатах и учитывая, что М1Î
. Записав это соотношение в координатах и учитывая, что М1Î  после элементарных преобразований, получим:
после элементарных преобразований, получим:


Заключение.
В течение весьма продолжительного времени и математики и физики были убеждены, что геометрия Евклида дает единственно правильное описание свойств реального пространства. Первым выступил с сообщением в печати об открытии новой – неевклидовой геометрии Н.И.Лобачевский.
Начиная со второй половины XIX столетия, исследования крупнейших учёных того времени показали, что неевклидова геометрия является системой логически столь же безупречной и внутренне непротиворечивой, как и система Евклида.
Евклидова геометрия возникла как отражение фактов действительности. Геометрия n- мерного евклидова пространства можно рассматривать в качестве примера абстрактной геометрической теории. Она строится путём простого обобщения основных положений обычной геометрии.
Применение евклидовой геометрии представляет самое обычное явление всюду, где определяются площади, объемы. Вся техника, поскольку в ней играют роль формы и размеры тел, пользуется евклидовой геометрией. Картография, геодезия, астрономия, все графические методы, механика немыслимы без геометрии. Глубокое применение евклидовой геометрии представляет геометрическая кристаллография, послужившая источником и областью приложения теории правильных систем фигур.
Литература
1) Атанасян Л.С., Гуревич Г.Б. «Геометрия» ч.1. М. Просвещение, 1973г.
2) Атанасян Л.С., Гуревич Г.Б. «Геометрия» ч.2. М. Просвещение, 1976г.
3) Атанасян Л.С., Базылев В.Т. «Геометрия» ч.1. М. Просвещение, 1986г.
4) Атанасян Л.С., Базылев В.Т. «Геометрия» ч.2. М. Просвещение, 1987г.
5) Атанасян Л.С., Атанасян В.А. «Сборник задач по геометрии» ч.1. М. Просвещение, 1973г.
6) Атанасян Л.С. «Сборник задач по геометрии» ч.2. М. Просвещение, 1975г.
7) Базылев В.Т. «Сборник задач по геометрии», М. Просвещение, 1980г.
8) Выгодский М.Я. «Справочник по высшей математике», М. 1962г.
9) Строик Д.Я. «Краткий очерк истории математики», М. Просвещение, 1975г.
10) Фетисов Л.И. «Очерки по евклидовой и неевклидовой геометрии», М. Просвещение, 1965г.
11) Математический энциклопедический словарь, М. Советская энциклопедия, 1988г.
|
из
5.00
|
Обсуждение в статье: Квадрики в евклидовом n – пространстве. |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

