Элементарные катастрофы

Существуют различные подходы к рассмотрению элементарных катастроф.

Арнольд В.И. на основе выводов теории особенности рассматривает простые образы вроде складки, сборки, точки возврата и еще несколько образов, получивших собственные имена, например, «ласточкин хвост».

Кузнецов А.П. рассматривает примеры систем с катастрофами (катастрофы складки и сборки), при выявлении существенных параметров, классификации критических точек.

Найман Э. вводит элементарные катастрофы в теории хаоса в качестве доказательства невозможности предсказать постоянные нелинейные и нерегулярные сложные движения, возникающие в динамической системе.

 Воспользуемся классификацией Тома Р., которая является таблицей элементарных катастроф и содержит в каждой своей строке две функции: росток катастроф  CG ( l ) и ее возмущением Pert ( l , k )

Таблица 1. Элементарные катастрофы Тома [5.C.67].

Тип катастрофы	k	Росток	Возмущение
А2	1	x 3	а1х
А±3	2	±х4	a 1 x + а2хг
А4	3	x 5	а1х + а2х2 + a 3 x 3 ■а3х3
A ±5	4	±х4	а1х + а2х2 + a3x3+ a4x4
А6	5	x7	а1х + а2х2 + a 3 x 3 + a 4 x 4 + a 5 x 5
D+4	3	x2y+y3	а1х + а2 y + a3y2
D5	4	x2y+y4 2 у + у*	а1х + а2 y + a3x2+ a4y2   Ь сцу2
D+6	5	x2y+y5 г У + Уъ	а 1 х + а 2 y + a3x2+ a4y2+a5y3
Е± 6	5	x3+ y4	а1х + а 2 y + a3xy+ a4y2+a5xy2

Проанализируем  каждый тип катастроф.

 

 

Катастрофы типа А₂

Предположим, что U ( x ₁ ..., х_п; с) — общее 1-параметриче­ское семейство потенциальных функций. Тогда при исследова­нии этого семейства можно встретить отдельные функции, кото­рые имеют неморсовские критические точки. Ограничимся изучением зависимости качественных изменений в поведении функции катастрофы F ( x ; a ) от управляющих параметров. Катастрофа А₂ задается формулой (7) и графически представлена на рис. 7.

А₂: F ( x ; a ) =1/3 x ³ + ax ,                                              (13)

Коэффициенты в простых ростках катастроф могут быть выбраны равными каноническим значениям, например, ±1 [5.C.67].

   В тех случаях, когда берутся производные, могут быть вы­браны другие канонические значения с помощью изменения масштабов. Для удобства такие же множители могут быть введены и в возмущение [5.C.67].                                 

Критические и дважды вырожденные критические  точки функции

F ( x ; а) определяются   соответственно из условий равенства нулю гра­диента

F { x ; а) и  d ² F / dx ² = 0, следовательно    х²+ а=0 и 2х=0.                               (14)

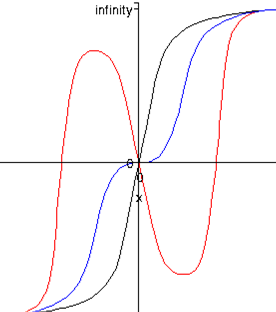a>0

a<0

a=0

 

Рис.7.  Все функции F(x;a)

Рассмотрим полную потенциальную энергию – U ( Q ). Точки, соответствующие максимуму и минимуму потенциальной энергии, это точки в которых, в которых dU / dQ обращается в нуль. При этом функция U = U ( q , q ) имеет только одну активную координату [1.C.24]. При построении модели (рис. 8) трансформация энергии обозначим Q и L общие переменные, заменяющие локальные переменные, которые обозначались строчными буквами q и  q. Полученное слиянии и исчезновении минимума и максимума, под действием единственного управляющего параметра, называется катастрофой складки. [1.C.25]. Ей соответствует траектория равновесия XCY , которая загибается в критической точке С, меняя при этом характер устойчивости.

Рис.8. Изменение энергии в случае катастрофы складки.

Покажем, что катастрофа типа А₂ представлена складкой.

На горизонтальной плоскости-проекции выделяется полукубическая парабола с точкой возврата (острием) в начале координат. Эта кривая делит горизонтальную плоскость на две части  (условно на меньшую и большую).

Точки меньшей части имеют по три прообраза (в них проекти­руется три точки поверхности), точки большей части — лишь по одному, точки кривой — по два.

При подходе к кривой из меньшей части два прообраза (из трех) сли­ваются и исчезают (в этом месте особенность — складка), при подходе к острию сливаются все три прообраза [5.C.69].

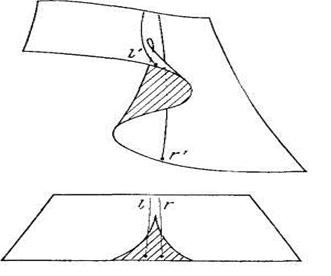
Рис.9. Катастрофа складки.

При изменении параметра выделяются  особые или бифуркационные значения параметра (рис.9). Вне  этих значений положения равновесия гладко зависят  от параметров [5.C.70].

 

Катастрофы типа А₃

Критические, дважды вырожденные критические и трижды вырожденные критические точки катастрофы А₃ определяются приравниванием соответственно первой, второй и третьей производных

F ( x ; a , b ) нулю: сепаратриса катастрофы, определяемая уравнениями

dF / dx = 0, dF ² / dx ² = 0, разделяет пространство управляющих параметров на две открытые области, представляющие функции с одной критической точкой или функции с тремя критическими точками.

Катастрофа типа А₃ задается следующим семейством функ­ций, зависящих от двух управляющих параметров а и b :

 А₊₃: F ( x ; a , b ) = + x ⁴ + ax + bx ² .                                                                        (15)

Гра­фик функции (рис.10) при различных зна­чениях управляющих параметров (а, b ): внутри области имеет форму сборки или симметричной бифуркации.

 

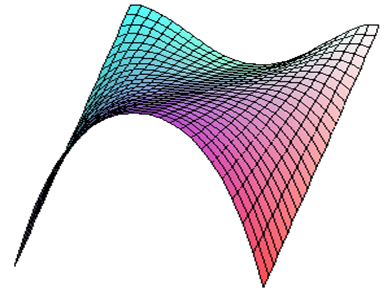
Рис. 10. График функции F(x;a,b) = +x⁴+ ax+bx².

F ( x ; a , b ) имеет три изолированные крити­ческие точки, а вне этой области — всего одну; на границе функция семейства имеет изолированную критическую точку и дважды вырожденную критическую точку, а в начале коорди­нат— трижды вырожденную критическую точку. Положение критических точек находится путем решения кубического урав­нения вида

gradF = x ³ + ax + b = 0. (16)                                                                            

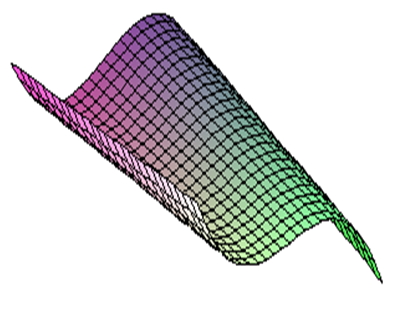
Рис. 11. График функции F = x³ + ax + b = 0.

Катастрофы типа А₄

Катастрофа типа А₄ задается следующим семейством функ­ций, зависящих от трех управляющих параметров а, b , с:

 А₄: F ( x ; a , b , c )= x ⁵ + ax + bx ² +сх³.                                                                    (17)

Критические точки определяются через приравненные к нулю производные:                             

1. Критические точки:         5х⁴ + а + 2 b х + 3х²с = 0.    

2. Дважды вырожденные: 10х³+ b +3х =0.  

3. Трижды вырожденные:    1 0x²+ 1=0.       

4. Четырежды вырожденные:   x =0.

Функция  А₄: F ( x ;0,0,0) имеет четырежды выраженную точку х=0.   

                       

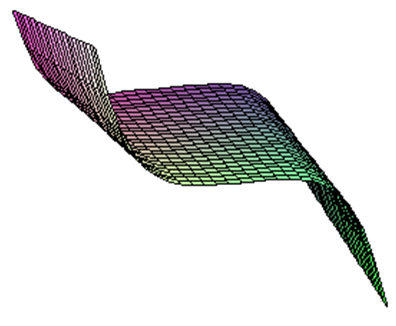
Рис. 13. График функции F(x;a,b,c)=x⁵+ ax+bx²+сх³.

Катастрофы типа A ₊₅

Катастрофа типа А₊₅ задается следующим семейством функ­ций, зависящих от четырех управляющих параметров а, b , с, d :

 А₊₅: F ( x ; a , b , c , d )= + x ⁴ +ах+ bx ² +сх³+ dx ⁴ . (15)                      

1. Критические точки:   +4х³+х+2 b х+3 cx ² +4 dx ³ =0             

2. Дважды вырожденные: +6х²+ b +3 cx +6 dx ² =0      

3. Трижды вырожденные: +4 a х+ c +4 dx =0  

       

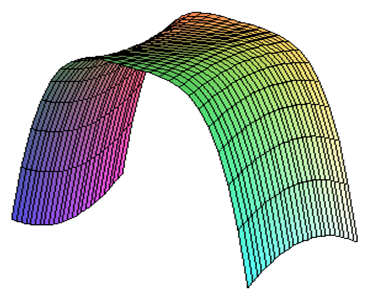
Рис. 14. График функции F(x; a, b, c) =+x⁴+bx²+сх³+dx⁴ .

Катастрофы типа A ₆

Катастрофа типа А₆ задается следующим семейством функ­ций, зависящих от пяти управляющих параметров а, b , с, d , e :

А₆: F ( x ; a , b , c )=х⁷+ а x + bx ² +сх³+ dx ⁴ + ex ⁵ (19)                      

1. Критические точки:  7х⁶+ a +2 b х+3 c х²+4 dx ³ +5 ex ⁴ =0.

2. Дважды вырожденные: 24х⁵+ b +3 c х+6 d х²+10 ex ³ =0.

3. Трижды вырожденные: 40х⁴+ c +4 dx +10 ex ² =0.   

4. Четырежды вырожденные: 40х³+ d +5 ex =0.        

5. Пяти вырожденные:           24 х²+ ex =0.   

6. Шести вырожденные:    48х+е=0.

                 

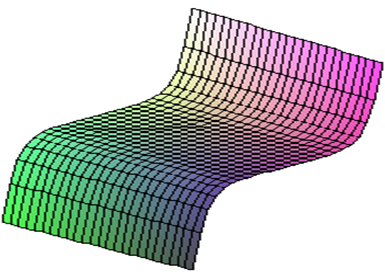
Рис. 15. График функции F(x; a, b, c) = х⁷+ аx+bx²+сх³+dx⁴+ex⁵.

Катастрофы типа D _{+ 4}

Катастрофа типа D₊₄ задается следующим семейством функ­ций, зависящих от трех управляющих параметров а, b , с:

D₊₄: F(x,y;a,b,c)= x²y+ y²+ ах +by + cy²=0.                                    (20)                                                                                 

 

                               

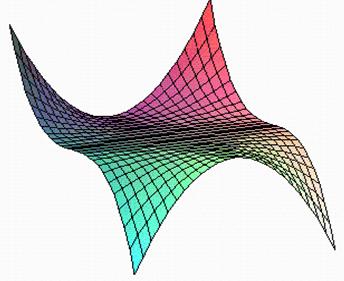
Рис. 16. График функции F(x; a, b, c) = x²y+ y²+ах+by+ cy²=0.

Катастрофы типа D ₅

Катастрофа типа А₊₅ задается следующим семейством функ­ций, зависящих от четырех управляющих параметров а, b , с, d :

 D ₅ : F ( x ; a , b , c , d )= х²у+у⁴+ ax + b у+ cx ² + d у².                            (22)                      

                    

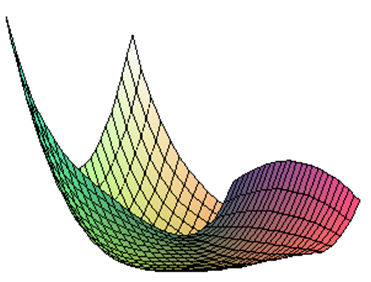
Рис. 17. График функции F(x;a ,b, c, d)= х²у+у⁴+ ax+bу+cx²+dу².

Катастрофы типа D _-6

Катастрофа типа D_-6 задается следующим семейством функ­ций, зависящих от пяти управляющих параметров а, b , с, d , e :

D _{- 6} : F ( x ; a , b , c , d )= х²у+у⁵+ ax + b у+ cx ² + d у²+ ey ³ .                             (23)                      

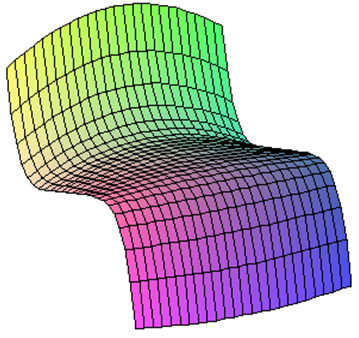
Рис. 18. График функции F(x;a ,b, c, d)= х²у+у⁵+ ax+bу+cx²+dу²+ey³.

 

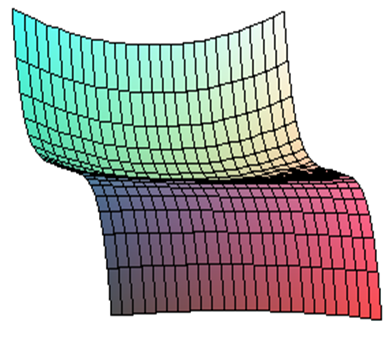
Рис. 19. График функции F(x; a, b, c, d) = х²у+у⁵+ ax+bу+cx²+dу²+ey³.

Катастрофы типа E₊₆

Катастрофа типа E₊₆ задается следующим семейством функ­ций, зависящих от пяти управляющих параметров а, b , с, d , e :

E₊₆: F ( x ; a , b , c , d , e )= х³+у⁴+ ax + b у+ cxy + d у²+ exy ² .                          (24)          

                      

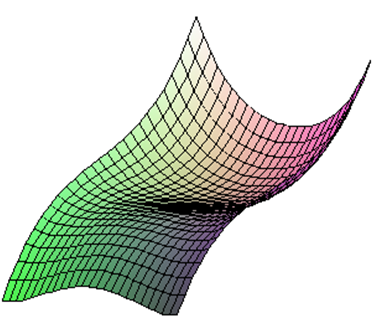
Рис. 20. График функции F(x;a ,b, c, d,e)= х³+у⁴+ ax+bу+cxy+dу²+exy².

 

Установле­ние наличия и типа катастрофы в рассмотренных выше случаях возрастаю­щей неопределенности в описании системы могут помочь определить упрощенную модельную потенциальную функцию, зависящую только от существенных переменных состояния и управляющих параметров. Cответствующий росток потенциальной  функции может помочь установить соответствующий тип уравнений, и то, каким образом потенциальная функция может входить в такие уравнения. 

 

Хотя катастрофы обнаруживаются при качественных исследованиях уравнений, существует эффект обратной связи, который иногда позволяет получить качественные следствия даже в том случае, когда мы не знаем самих уравнений при условии, что мы в состоянии установить их наличие и тип катастрофы [2.C.144].

Среди огромного количества катастроф можно выделить ряд характеристик, позволяющие говорить о наличии катастрофы.

1. Модальность.

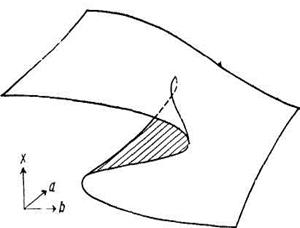
Рис. 21. Катастрофа сборки.

Физическая система может иметь два или более различных физических состояния. Другими словами, описывающая систему потенциальная функция имеет более чем один локальный мини­мум в некоторой области изменения внешних управляющих параметров.

Катастрофа сборки становится бимодальной, если управляющие параметры лежат в пределах области сборки.

 

2. Недостижимость.

Если система находится в состоянии равновесия, которое оказывается морсовским i-седлом (рис.22), то такое состояние является неустойчивым, поскольку существуют инфинитезимальные возмущения, приводящие к уменьшению значения по­тенциала. Всякий раз, когда потенциальная функция имеет бо­лее чем один локальный минимум, она должна иметь, по край­ней мере, одно i-седло (с>0), которое является состоянием неустойчивого равновесия [4.C.83].

Два слоя в области сборки, представляющие локально устойчивые минимумы, разделены срединным недостижимым слоем, представ­ляющим неустойчивые локальные максимумы.

 

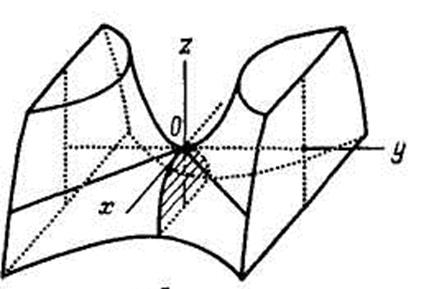Рис. 22. Морсовское седло.

3. Катастрофические скачки.

Малые изменения в зна­чениях управляющих параметров могут вызывать большие из­менения («катастрофический скачок») в значениях переменных состояния по мере того, как система перескакивает из одного локального минимума в другой [5.C.3]. Согласно принципу Максвелла, этот неожиданный скачок сопровождается плавным, но не дифференцируемым изменением значений потенциала. Переход из окрестности одного локального минимума в другой проявляет себя в большом изменении значения переменной состояния, которое часто происходит в сверхбыстрой временной шкале. Свойства устойчивости критических точек функции ката­строфы-сборки легко определяют­ся из рассмотрения многообразия этой катастрофы. Неожиданный скачок в значении переменной состояния происходит, как только состояние системы перескакивает с одного слоя поверхности ка­тастрофы сборки на другой (рис.23).

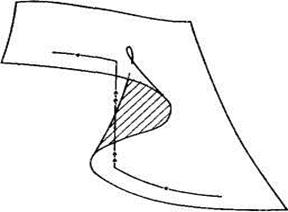
Рис.23. Катастрофа сборки.

4. Расходимость.

Конечные изменения в значении управляющих параметров приводят к конечным изменениям в значениях переменных со­стояния в точке равновесия [5.C.87]. Обычно малые возмущения в исход­ных значениях управляющих параметров ведут лишь к неболь­шому изменению начальных и конечных значений переменных состояния. Однако в окрестности неморсовской критической точки малые изменения начальных значений переменных состояния могут привести к большим изменениям конечных значений этих переменных.

Неустойчивость физического процесса при возмущениях в траектории управляющих параметров назы­вается расходимостью.

Расходимость в случае катастрофы сборки. Два близких пути в пространстве управляющих парамет­ров могут приводить к далеко расходящимся конечным значениям переменных состояния (рис.24).

 

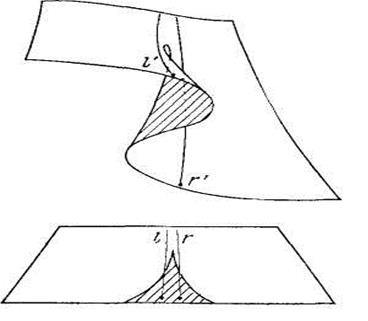
Рис.24 . Катастрофа сборки.

5. Гистерезис.

Гистерезис имеет место, когда физический процесс не яв­ляется полностью обратимым, т. е. над той же самой точкой пространства управляющих параметров скачок из локального минимума 1 в локальный минимум 2 может и не произойти, в то время как скачок из локального минимума 2 в локальный ми­нимум 1 имел место [2.C.113].

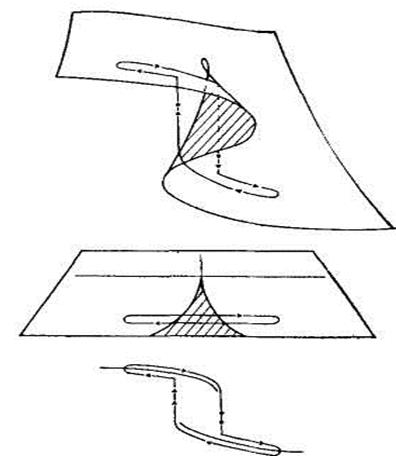
Рис.25. Явление гистерезиса.

Явление гистерезиса имеет место, когда скачок с одного листа на другой не случается при тех же значе­ниях управляющих парамет­ров, что и возвратный скачок.

Модальность, недостижимость, катастрофиче­ские скачки, расходимость и гистерезис обычно встречаются в совокупности. Они зависят от достижимости физической систе­мой области пространства управляющих переменных, в которой потенциал имеет более чем один локальный минимум. Явление гистерезиса может быть не наблюдаемо, если поведение системы подчиняется принципу Максвелла, однако даже в этом случае иногда возможно наблюдать его (сверхохлаждение, сверхнагре­вание) с помощью экспериментальных методов [5.C.93].

Глава 2.ПРИМЕНЕНИЕ ТЕОРИИ КАТАСТРОФ

В теории катастроф есть нечто таинственное – это удивительные

совпадения связей между далекими на первый взгляд предметами теориями [7.С.62].

Теория катастроф дает универсальный ме­тод исследования скачкообразных переходов, разрывов, внезапных качественных изменений. Существуют различные публикации, в которых теории катастроф применяется к исследованиям биения сердца, в геометрической и физической оптике, эмбриологии, лингвистике, психологии, экономике, гид­родинамике, геологии и теории элементарных частиц.  Среди опубликованных работ по теории катастроф есть исследования устойчивости кораблей, моделирования дея­тельности мозга и психических расстройств, восстаний заключенных в тюрьмах, поведения биржевых игроков, влияния алкоголя на водителей транспортных средств [3.C.7].

Кроме того, явления устойчивости представляют огромный интерес для всех научных работников и инженеров из самых разных областей науки и техники. Например,  потеря устойчивости тонкостенных конструкций под действием веса и ветровой нагрузки, астрофизика коллапсирующих звезд, внезапное разрушение кристаллической решетки, фазовые переходы в термодинамических системах, взрывное развитие популяций конкурирующих экологических видов, возникновение турбулентности в быстро движущейся жидкости, хаотическое движение в простых детерминистических моделях, управление положением космического корабля и нейродинамика мозга.

Общая точка зрения на все эти различные проблемы устойчивости достигается при помощи теории катастроф. Чтобы понять предмет достаточно глубоко, требуется некоторое знание математики, только тогда  

можно составить правильное представление об области применения теории катастроф[2.C.12]