Математическое моделирование динамических систем

При математическом моделировании исследование динамики работы оборудования осуществляется на основе изучения поведения его математической модели. Построение такой модели базируется на расчетной схеме исследуемого объекта, а также принятых ограничениях и допущениях. Большинство математических моделей динамических систем представляют собой систему дифференциальных уравнений, отражающих физические процессы в объекте. Рассмотрим математическую модель гидравлического пресса на макроуровне, как гидромеханической системы [31]. В качестве её элементов выбираются функциональные узлы пресса, для которых модель описывается на основании уравнений движения масс (структурные компоненты), уравнений связи масс в единую систему (топологические компоненты) и принципа Даламбера. В общем случае такая модель имеет вид:

( 1.1)

где ‑масса i^го элемента;

, , ‑перемещение, скорость и ускорение i^го элемента;

 - жёсткость k^го элемента; t - время;

 - обобщенная сила, действующая на i^ый элемент.

На рисунке 1.2 приведена типичная расчётная схема гидравлического пресса. Расчётная схема представлена колебательной системой с одной степенью свободы.

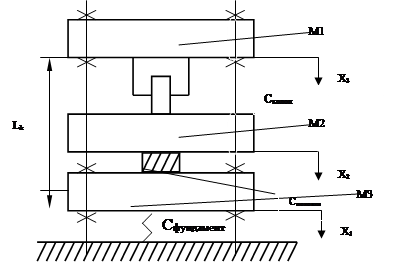
Рисунок 1.2 – Пример расчётной схемы гидравлического пресса

Колебательная система состоит из трёх масс – М1, М2, М3; и из трёх элементов на расчётной схеме представленными пружинами с соответствующими жестокостями: C_{фундамента}, C_{поковки}, C_колоп. Система дифференциальных уравнений описывающих данную модель будет выглядеть следующим образом:

(1.2)

В зависимости от сложности описания динамической системы можно условно выделить два направления изучения происходящих в ней процессов: аналитическое и численное [31,32]. При решении конкретных задач, в случае невозможности получения точного аналитического решения при учёте всех существенных факторов, принимается целый ряд допущений, отражающихся на адекватности модели. Например, при моделировании работы гидравлических прессов, в большинстве случаев, силы, действующие на элементы конструкции, полагаются постоянными во времени, не учитываются изменения жёсткости, зазоры, волновые процессы в гидросистеме (т.к. это повлекло бы за собой необходимость совместного решения системы дифференциальных обычных и волновых уравнений в частных производных) В таком случае аналитическое решение системы (1.3) можно представить в виде:

 (1.3)

где параметры  и  определяются начальными условиями вида:

.

Следует отметить, что хотя такой метод и дает достаточно точное аналитическое решение, но на практике его применение ограничено моделированием достаточно простых объектов, содержащих максимум три‑четыре элемента [33,34].