Базис и отделимость топологического пространства

Определение 1. Пусть (Х, Ф) – топологическое пространство, и пусть G^* ={G } – некоторое семейство открытых множеств в этом пространстве. Если любое открытое множество в (Х, Ф) представимо в виде объединения некоторых множеств G^*, то G^* называется базисом топологического пространства (Х, Ф) или базой.

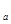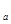Теорема 1. Для того, чтобы семейство G^* ={G } Ì F было базисом топологического пространства (Х, Ф) необходимо и достаточно, чтобы для любой точки Î Х и любой её окрестности U_a существовало множество G_a Î G^* такое, что Î G_a  и G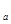_a Ì U_a.

Теорема 2. Для того, чтобы семейство подмножеств G^* = {G } было базисом некоторого топологического пространства Х необходимо и достаточно, чтобы для любых двух элементов U_, V Î G^* и каждой точки хÎ U Ç V существовал такой элемент W Î G^*, что х Î W и W Ì U Ç V. При этом Æ Î G^* и G  = X.

Доказательство. 1. Пусть G^* – база. Тогда, так как U Ç V – открытое множество, то согласно теореме 1 существует W такое, что W Î G^* и х Î W Ì U Ç V.

2. Докажем обратное утверждение. Пусть G^* – семейство с выделенными нами специальными свойствами. В-семейство всевозможных объединений элементов из G^*. Покажем, что В-топология. Ясно, что объединение любой совокупности элементов из В является объединением элементов из G^*, а, следовательно, принадлежит В.

Пересечение любых двух элементов U и V из В также принадлежит В.

Действительно, если х₀ Î U Ç V, то существует U¢ Î G^* и V¢ Î G^* такие, что U^¢ Ì U, V¢ Ì V и х₀ Î U¢ Ç V¢. Тогда по условию существует

W Î G^*, для которого

х₀ Î W Ì U¢ Ç V¢ Ì U Ç V.

Но, тогда

U Ç V =  Î В.

Кроме того,

Х = G  Î В.

Итак, В-топология, а G^* её базис.

Теорема доказана.

Из предыдущих теорем следует, что не всякое семейство G^* может служить базой топологии. Возникает вопрос: можно ли по произвольному семейству {G_i} множеств определить некоторую топологию? Эта топология должна быть определена на множестве Х, являющимся объединением всех элементов {G_i}, каждый элемент из {G_i} должен быть открыт в этой топологии.

Кроме того, возникает вопрос: существует ли наименьшая топология на Х, содержащая {G_i}? На этот вопрос отвечает следующая теорема.

Теорема 3. Пусть G^* = {G_i} – произвольное непустое семейство множеств. Тогда семейство всевозможных конечных пересечений элементов из G^* образует базу некоторой топологии на множестве Х =  G_i.

Доказательство. Обозначим В-семейство всевозможных конечных пересечений элементов из G^*. Тогда пересечение любых двух элементов из В снова является элементом В. В силу теоремы 2 получим, что В-база некоторой топологии.

Теорема доказана.

У пространств, топология которых обладает счетной базой, есть много хороших свойств.

Примеры. 1. В любом топологическом пространстве (Х, Ф) множество Ф – база (очевидно).

2. (R, ),  – топология, заданная метрикой.

G^* = {Æ, всевозможные интервалы} – база.

3. (Х. Ф) дискретная топология.

G^* = {Æ} È {{х}| х Î Х} – база.

Аксиома отделимости

Наличие хороших свойств пространства зависит от возможности отделить одну точку от другой с помощью окрестностей этих точек.

Поэтому, обычно, рассматривают такие топологические пространства, которые удовлетворяют дополнительным условиям, например, так называемым аксиомам отделимости.

Аксиома Хаусдорфа

Для любых двух различных точек пространства существуют их непересекающиеся окрестности.

Топологические пространства, в которых выполняется аксиома Хаусдорфа, называют хаусдорфовыми пространствами.

Нетрудно доказать, что любое подпространство хаусдорфова пространства, содержащее не менее двух различных точек, также является хаусдорфовым пространством.

В любом топологическом пространстве можно рассмотреть сходящуюся последовательность точек.

Однако, понятие предела удобно лишь там, где сходящаяся последовательность имеет единственный предел.

Оказывается, аксиома 2 является необходимым и достаточным условием единственности предела сходящейся последовательности.

Пусть в топологическом пространстве (Х, Ф) дана последовательность точек х₁, х₂, …, х_n, … точка х₀ называется пределом этой последовательности, если для любой окрестности U_x0 точки х₀ найдётся такой номер n₀, что для всех n > n₀ точки х_n Î U_x0.

При этом последовательность точек {х_n} называется сходящейся к точке х₀.

Теорема 4. В хаусдорфовом пространстве (Х, Ф) сходящаяся последовательность точек {х_n} имеет единственный предел.

Пример 1. В силу теоремы 2 § 1 любое топологическое пространство, топология которого порождена метрикой, является хаусдорфовым пространством.

Пример 2. Двуточечное топологическое пространство

Х = , Ф = {Æ, Х, }

не является хаусдорфовым пространством.

Действительно, рассмотрим точки  и . Для них нет непересекающихся окрестностей, так как окрестностью точки  является сама точка  или все Х, а окрестностью точки  будет только Х.

Очевидно, Ç Х =  и предложение доказано.