Топологические преобразования топологических пространств

Непрерывные отображения

Пусть даны топологические пространства (Х, Ф), (У, W) и отображение

: X ® У.

Определение 1. Отображение : X ® У называется непрерывным в точке х₀ Î Х, если для каждой окрестности V точки f(x₀) существует такая окрестность U точки х₀, что (U) Ì V.

Определение 2. Отображение : X ® У называется непрерывным на множестве Н Ì Х, если  непрерывно в каждой его точке.

Если Н = Х, то говорят, что  непрерывно на Х.

Определение 3. Если : X ® У, В Ì У, то множество всех точек х₀ Î Х, для каждой из которых имеем (x₀) Î В называется прообразом множества В, и обозначается ^-1(B), причем имеет место

( ^-1(B)) Ì B.

Теорема 1. Для того, чтобы отображение : X ® У было непрерывным на Х, необходимо и достаточно, чтобы прообраз любого открытого (замкнутого) множества был открытым (замкнутым) множеством.

Доказательство. 1. Необходимость.

Пусть : Х ® У непрерывно, V открытое множество в У, а

U = ^-1(V).

Докажем, что U – открытое множество в Х. Пусть  – любая точка из U и b = ( ). Множество V является окрестностью точки b. Так как  – непрерывно, то найдётся окрестностью U  точки , что (U ) Ì V.

Очевидно,

U  Ì ^-1(V) = U.

Так как U =  U , то U – открытое множество.

Достаточность. Возьмём любую точку  Î Х и пусть b = ( ). Если V – произвольная окрестность точки b, то U = ^-1(V) открытое множество и является окрестностью точки . Поскольку (U) Ì V, то  – непрерывно в точке , что требовалось доказать.

Для замкнутых множеств теорема доказывается переходом к дополнительным множествам.

Замечание. При непрерывном отображении образ замкнутого

(открытого) множества может быть не замкнутым (не открытым) множеством.

Теорема 2. Пусть X, Y, Z – топологические пространства.

Если отображения f  и g  непрерывны, то непрерывна и их композиция:

g ×f: Х ® Z.

Доказательство. Пусть W открытое множество пространства Z. Так как g – непрерывно, то по предыдущей теореме

G ^-1(W) = V – открыто в У.

Тогда аналогично, U = f^-1(V) – открыто в Х.

Но U = f ^-1 (g ^-1(W)) = (g×f) ^-1(W) – прообраз W.

Теорема доказана.

Пример непрерывного отображения

Рассмотрим плоскость П и прямую ℓ Ì П с естественными топологиями. Докажем, что ортогональное проектирование : П ® ℓ является непрерывным отображением.

Действительно, пусть для произвольной точки А Î П

 (А) = А_0.

Пусть V– -окрестность точки А₀, то есть V – интервал.

В точке А рассмотрим открытый круг радиуса d = 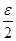, то есть окрестность U точки А. Очевидно,  (U) Ì V и, следовательно,

– является непрерывным отображением в точке А.

Так как А – произвольная точка плоскости П, то  – непрерывное отображение.