Связность топологических пространств

Определение 1. Топологическое пространство (Х, Ф) называется несвязным, если существуют два непустых открытых множества U и V таких, что U È V = Х и U Ç V = Æ.

Другими словами топологическое пространство (Х, Ф) может быть разбито на два непустых открытых множества, не имеющих между собой общих точек.

Топологическое пространство (Х, Ф) называется связным, если не существует такого разбиения.

Пример. Х= ( , b), (X, Ф) – связное топологическое пространство, если Ф = {Æ, Х, } и, если Ф = {Æ, Х, , b} – то это пример несвязного топологического пространства.

Заметим, что если несвязное пространство Х разбито на два непустых открытых множества U и V, U Ç V = Æ, то U = C_x V и V = C_x U.

Поэтому U и V – замкнутые множества.

Отсюда получаем необходимые и достаточные условия.

Теорема 1. Топологическое пространство (X, Ф) будет связным тогда и только тогда, когда в нем одновременно открытым и замкнутым множеством являются лишь само пространство или пустое множество.

Определение 2. Множество М в топологическом пространстве называется связным, если оно является связным пространством относительно индуцированной топологии, то есть связно определяемое им подпространство.

Другими словами, множество М в топологическом пространстве Х называется связным, если нельзя найти двух открытых в Х множеств G₁ и G₂ таких, что

1. (G₁ Ç М) È (G₂ Ç М) = М.

2. (G₁ Ç М) Ç (G₂ Ç М) = Æ.

3. G₁ Ç М ¹ Æ, G₂ Ç М ¹ Æ.

Теорема 2. В топологическом пространстве (Х, Ф) замыкание связного множества – связно.

Теорема 3. Если А и В два открытых множества в (Х, Ф), причем

А Ç В = Æ

и непустое связное множество

H Ì A È B,

то H Ì A, или H Ì В.

Теорема 4. Пусть { } – совокупность связных подмножеств в пространстве (Х, Ф), имеющих общую точку. Тогда множество H =  также будет связным в (Х, Ф).

Теорема 5. Компоненты двух различных точек либо не пересекаются, либо совпадают.

Теперь мы можем говорить просто о компонентах пространства, на которые они распадаются.

Теорема 6. Компонента топологического пространства (Х, Ф) является замкнутым множеством.

Доказательство. Пусть Н – компонента топологического пространства (Х, Ф), и  – некоторая ее точка.

Очевидно

Н Ì ,

В силу теоремы 2 множество  – связно и так как  Î , то

 Ì Н.

Поэтому

 = Н.

Замечание. Пусть топологическое пространство (Х, Ф) – несвязное, то есть существуют два непустых открытых множества U и V таких, что

U È V = Х

и

U Ç V = Æ.

Если при этом различные точки х и у принадлежат одной компоненте, то {x, y} Ì U или {x, y} Ì V.

Это утверждение вытекает из теоремы 3.

Определение 3. Областью называется непустое связное открытое множество топологического пространства.

Замкнутой областью называется такое замкнутое множество, которое является замыканием области.

Пример. Пусть Х – множество действительных чисел с топологией . Доказать, что любое подмножество  связно.

Доказательство. Рассмотрим произвольное подмножество . Пусть – непустое подмножество , открытое и замкнутое в 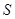. Тогда

 = ,

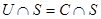где  открыто в , а  замкнуто в Х, т.е.  для некоторого , а  для некоторого . Так как

,

то для любого  выполнены неравенства  и .

Действительно, если найдется значение , то . Аналогично, если найдется значение , то .

Итак,  и , откуда следует, что  связно.