 |
Главная |
Простые зубчатые механизмы
|
из
5.00
|
7.1 Структурный анализ простого зубчатого механизма
Структурный анализ простых зубчатых механизмов сводится к определению подвижности механизма.

Таблица 9 - звенья простого зубчатого механизма
| № П.П | Номер звена | Вид совершаемого движения | схема | Кинематическое состояние |
| 1 | 1 | вращательное | 
| подвижное |
| 2 | 2 | вращательное | 
| подвижное |
Подвижность механизма определяемпо формуле Чебышева:

где  - подвижность механизма;
- подвижность механизма;
 - число подвижных звеньев;
- число подвижных звеньев;
 и
и  - соответственно число пар пятого и четвертого класса.
- соответственно число пар пятого и четвертого класса.
В структуру механизма входят два подвижных звена (Таблица 9) и стойка, представленная двумя шарнирно-неподвижными опорами. Следовательно,  =2.
=2.
Таблица 10 –кинематические пары простого зубчатого механизма
| Номер звена | схема | название | Класс / подвижность | Вид контакта / замыкание |
| 0-1 | 
| вращательная | 5/1 | По поверхности(низшая)/ геометрическое |
| 1-2 | 
| зубчатая | 4/2 | Линия (высшая)/ геометрическое |
| 0-2 | 
| вращательная | 5/1 | По поверхности(низшая)/ геометрическое |
Из таблицы 10 видно, что кинематические пары 0-1 и 0-2 являются вращательными парами пятого класса, следовательно, 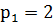 .
.
Кинематическая пара 1-2 является парой четвертого класса, следовательно,  .
.
Подставим число подвижных звеньев и число пар пятого и четвертого классов в формулу Чебышева:

Полученный результат означает, что для однозначного описания положения всех звеньев механизма в рассматриваемой плоскости достаточно знать одну обобщенную координату.
7.2 Синтез эвольвентного зацепления простого зубчатого механизма
Найдем инвалюту угла зацепления

По таблице значений инвалют найдем угол зацепления:

Найдем минимальную величину коэффициента смещения для шестерни:
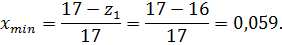
Найдем коэффициент смещения для колеса:

Примем значение  .
.
Отложим значение смещения  и
и  на осях блокирующего контура. Точка их пересечения должна находится в блокирующем контуре. В данном случае точка находится в контуре, следовательно оставляем полученные значения коэффициентов для дальнейших расчетов.
на осях блокирующего контура. Точка их пересечения должна находится в блокирующем контуре. В данном случае точка находится в контуре, следовательно оставляем полученные значения коэффициентов для дальнейших расчетов.
Найдем геометрические параметры зубчатых колес.
Диаметры делительных окружностей:
для шестерни 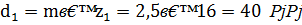
для колеса 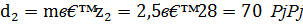
где  - модуль;
- модуль;
 - число зубьев на шестерне и колесе соответственно.
- число зубьев на шестерне и колесе соответственно.
Диаметры начальных окружностей:
для шестерни 
для колеса 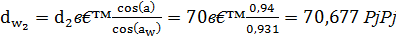
Шаг по делительной окружности:

Шаг по основной окружности:

Диаметры основных окружностей:
для шестерни 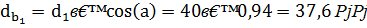
для колеса 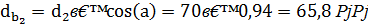
Диаметры окружностей впадин зубьев:
для шестерни
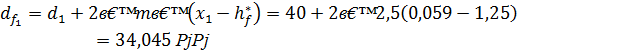
для колеса
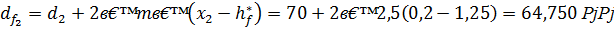
где  - коэффициент ножки зуба.
- коэффициент ножки зуба.
Диаметры окружностей вершин зубьев:
для шестерни 
для колеса 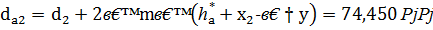
где  - коэффициент головки зуба.
- коэффициент головки зуба.
Коэффициент уравнительного смешения:

Коэффициент воспринимаемого смешения:
 .
.
Уточненное межосевое расстояние:

Делительное межосевое расстояние:

Толщина зуба по делительной окружности:
для шестерни :

для колеса :
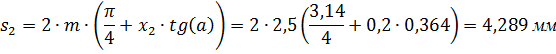
Толщина впадин по делительной окружности:
для шестерни 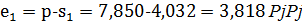
для колеса 
Высота зубьев:

Углы профиля на окружности вершин:
для шестерни: 
для колеса: 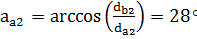
Толщина зубьев по окружности вершин:
для шестерни
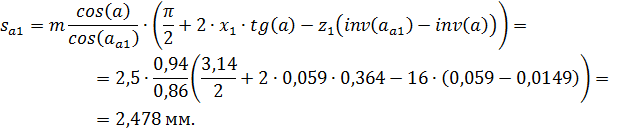
для колеса

Проверка:
 где
где 
Оба значения толщины зубьев по окружности больше значения минимальной толщины, проверка сходится.
Коэффициент торцевого перекрытия:

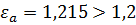
Для построения зубчатого зацепления определим масштабный коэффициент длин и переведем все геометрические параметры зубчатых колес в данный масштабный коэффициент, при условии, что высота зуба должна быть не менее  на чертеже.
на чертеже.
Переведем все значения через  :
:



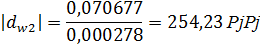


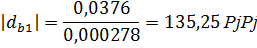
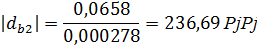


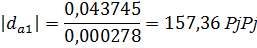
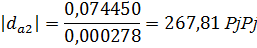







Для построения зубчатого зацепления отложим межосевое расстояние  . Проведем начальную, делительную, основную окружности, а также окружности вершин и впадин зубьев для каждого зубчатого колеса. Начальные окружности
. Проведем начальную, делительную, основную окружности, а также окружности вершин и впадин зубьев для каждого зубчатого колеса. Начальные окружности  и
и  должны сопрягаться в полюсе зацепления P. Откладываем под углом
должны сопрягаться в полюсе зацепления P. Откладываем под углом  от линии центров
от линии центров  для колеса и для шестерни лучи, пересекающие основные окружности в точках A и B. Через точки A и B проводим прямую - линию зацепления. Она проходит через полюс зацепления P. Отрезок от точки сопряжения P до точки пересечения A, делим на шесть равных частей
для колеса и для шестерни лучи, пересекающие основные окружности в точках A и B. Через точки A и B проводим прямую - линию зацепления. Она проходит через полюс зацепления P. Отрезок от точки сопряжения P до точки пересечения A, делим на шесть равных частей  . Проецируем полученные точки на основную окружность, проводим через каждую из них касательную к основной окружности, и на касательных откладываем величину отрезка PA, каждый раз уменьшая на величину
. Проецируем полученные точки на основную окружность, проводим через каждую из них касательную к основной окружности, и на касательных откладываем величину отрезка PA, каждый раз уменьшая на величину  . Полученные точки соединяем плавной кривой и получаем нижнюю половину эвольвентного профиля зуба. Аналогично построим вторую половину профиля зуба, только увеличивая отрезок PA на величину
. Полученные точки соединяем плавной кривой и получаем нижнюю половину эвольвентного профиля зуба. Аналогично построим вторую половину профиля зуба, только увеличивая отрезок PA на величину  . Откладываем толщину зуба по делительной окружности и ширину зуба по окружности вершин. Симметрично отобразим вторую половину профиля зуба. По делительной окружности откладывая ширину впадины и шаг, строим еще два - три зуба. Аналогично строим профили зубьев шестерни.
. Откладываем толщину зуба по делительной окружности и ширину зуба по окружности вершин. Симметрично отобразим вторую половину профиля зуба. По делительной окружности откладывая ширину впадины и шаг, строим еще два - три зуба. Аналогично строим профили зубьев шестерни.
|
из
5.00
|
Обсуждение в статье: Простые зубчатые механизмы |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

