Структура анализа главных компонентов

Следующим вопросом, подлежащим рассмотрению, является поиск тех единичных векторов q, для которых функция ψ(q) имеет экстремальные или стационарные значения (локальные максимумы и минимумы) при ограниченной Евклидовой норме вектора q. Решение этой задачи лежит в собственной структуре матрицы корреляции R. Если q — единичный вектор, такой, что дисперсионный зонд ψ(q) имеет экстремальное значение, то для любого возмущения 6q единичного вектора q выполняется!

 

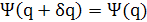                                                     (1.10)

 

Из определения дисперсионного зонда можем вывести следующее соотношение:

 

,

 

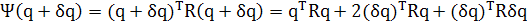где во второй строке использовалось выражение (1.8). Игнорируя слагаемое второго порядка (δq)TRδq и используя определение (1.9), можно записать следующее:

 

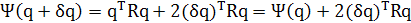(1.11)

 

Отсюда, подставляя (1.10) в (1.11), получим:

 

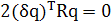,                                                           (1.12)

 

Естественно, любые возмущения δq вектора q нежелательны; ограничим их только теми возмущениями, для которых норма возмущенного вектора q+δq остается равной единице, т.е.

 

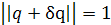
или, что эквивалентно,

 

,

 

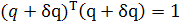Исходя из этого, в свете равенства (1.4) требуется, чтобы для возмущения первого порядка δq выполнялось соотношение

 

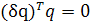                                                                (1.13)

 

Это значит, что возмущения δq должны быть ортогональны вектору q и, таким образом, допускаются только изменения в направлении вектора q.

Согласно соглашению, элементы единичного вектора q являются безразмерными в физическом смысле. Таким образом, можно скомбинировать (1.12) и (1.13), введя дополнительный масштабирующий множитель l, в последнее равенство с той же размерностью, что и вхождение в матрицу корреляции R. После этого можно записать следующее:

 

,

 

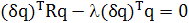или, эквивалентно,

 

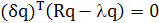,                  (1.14)

 

Для того чтобы выполнялось условие (1.14), необходимо и достаточно, чтобы

 

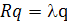                                       (1.15)

 

Это — уравнение определения таких единичных векторов q, для которых дисперсионный зонд ψ (q) принимает экстремальные значения.

В уравнении (1.15) можно легко узнать задачу определения собственных значений (eigenvalue: problem) из области линейной алгебры. Эта задача имеет нетривиальные решения (т.е. q ≠ 0) только для некоторых значений l, которые называются собственными значениями (eigenvalue) матрицы корреляции R. При этом соответствующие векторы q называют собственными векторами (eigenvector). Матрица корреляции характеризуется действительными, неотрицательными собственными значениями. Соответствующие собственные векторы являются единичными (если все собственные значения различны). Обозначим собственные значения матрицы R размерности т х т как l1, l2,,.., lm, а соответствующие им собственные векторы -q1, q2,...,qm соответственно. Тогда можно записать следующее:

 

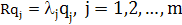                        (1.16)

 

Пусть соответствующие собственные значения упорядочены следующим образом:

 

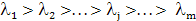 ,          (1.17)

 

При этом l1 будет равно lmax. Пусть из соответствующих собственных векторов построена следующая матрица размерности т х т:

 

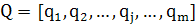            (1.18)

 

Тогда систему т уравнений (1.16) можно объединить в одно матричное уравнение:

 

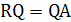                                      (1.19)

 

где А — диагональная матрица, состоящая из собственных значений матрицы R:

 

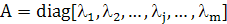      (1.20)

 

Матрица Q является ортогональной (унитарной) в том смысле, что векторы-столбцы (т.е. собственные векторы матрицы R) удовлетворяют условию ортогональности:

 

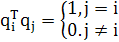                           (1.21)

 

Выражение (1.21) предполагает, что собственные значения различны. Эквивалентно, можно записать:

 

 

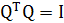
из чего можно заключить, что обращение матрицы Q эквивалентно ее транспонированию:

 

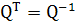                                     (1.22)

 

Это значит, что выражение (8.17) можно переписать в форме, называемой ортогональным преобразованием подобия (orthogonal similarity transformation):

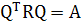                                   (1.23)

 

или в расширенной форме:

 

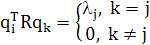                      (1.24)

 

Ортогональное преобразование подобия (1.23) трансформирует матрицу корреляции R в диагональную матрицу, состоящую из собственных значений. Сама матрица корреляции может быть выражена в терминах своих собственных векторов и собственных значений следующим образом:

 

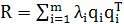                          (1.25)

 

Это выражение называют спектральной теоремой (spectral theorem). Произведение векторов 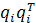имеет ранг 1 для всех i.

Уравнения (1.23) и (1.25) являются двумя эквивалентными представлениями разложения по собственным векторам (eigencomposition) матрицы корреляции R.

Анализ главных компонентов и разложение по собственным векторам матрицы R являются в сущности одним и тем же; различается только подход к задаче. Эта эквивалентность следует из уравнений (1.9) и (1.25), из которых ясно видно равенство собственных значений и дисперсионного зонда, т.е.

 

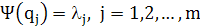           (1.26)

 

Теперь можно сделать выводы, касающиеся анализа главных компонентов.

• Собственные векторы матрицы корреляции R принадлежат случайному вектору X с нулевым средним значением и определяют единичные векторы q j, представляющие основные направления, вдоль которых дисперсионный зонд Ψ(qj) принимает экстремальные значения.

• Соответствующие собственные значения определяют экстремальные значения дисперсионного зонда Ψ(uj)