Оценивание по конечному числу наблюдений

До сих пор предполагалось, что все математические ожидания могут быть вычислены, т. е. известна совместная плотность распределения р (х1,, . . ., хт, у). Так бывает довольно редко. Обычно необходимо оценивать параметры, используя конечное число наблюдений, а именно выборочные значения. Таким образом, оценка должна быть функцией этих выборочных значений, которые фактически представляют собой наблюдаемые значения реализаций случайных величин. Это означает, что оценка тоже случайная величина и может быть охарактеризована плотностью вероятности. Качество оценки зависит от этой функции и, в частности, от среднего значения и дисперсии.

Излагаемые методы имеют длинную историю. Уже в 1795 г. Гаусс использовал их при исследовании движения планет. В наши дни они применяются, например, при определении параметров орбит спутников. Следует отметить что, помимо обычных регрессионных моделей

 

 

где ni — случайная величина, в литературе рассматриваются также авторегрессионная модель

 

 

и обобщенная регрессионная модель

 

 

Обозначения. Теперь посмотрим, как получаются оценки. Пусть наблюдается выходной сигнал объекта у, который состоит из отклика на входное воздействие и, шума объекта и ошибок измерений. В момент j-го измерения выходной сигнал имеет вид

 

                      (2.1)

 

Вектором b обозначена зависимость выборочных значений от компонент вектора параметров объекта b 0, b 1: . . ., b т. Определим

 

                               (2.2)

 

Шум зададим его математическим ожиданием и ковариационной матрицей:

 

 (2.3)

                 (2.4)

 

Задача состоит в том, чтобы определить оценку β вектора параметров Ь. Для этого используется теоретически предсказываемый выходной сигнал w, т. е. выход модели, который зависит от вектора коэффициентов β = (β0, βi,...,β m). Эта функциональная зависимость может быть выбрана различными способами. Простейшей является линейная функциональная связь между w и J (линейная по параметрам модель)

 

где ui(j)— известные линейно независимые функции. Запишем w в виде

 

                                        (2.5)

 

где

 

          (2.6)

 

Снова заметим, что такой выбор линейной связи между w и Р не означает того, что связь между входом и выходом модели должна быть линейной, Предполагается, что матрица U полностью известна, т. е. может быть измерена без ошибок. Кроме того, предполагается, что число наблюдений к превышает число т + 1 неизвестных параметров.

Класс линейных несмещенных оценок определяется следующими свойствами:

 

                 (2.7)

 

где Q — (т + 1) x k-матрица, и

 

                                         (2.8)

 

Предполагается, что равенство (2.5) может дать полное описание объекта, т.е.

 

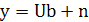                                           (2.9)

 

Допустим сначала, что U и n статистически независимы. Теперь вектор ошибки е можно определить как

 

                             (2.10)

 

В качестве функции ошибок или функции потерь можно выбрать положительно определенную форму

 

                                (2.11)

 

где R- матрица весовых коэффициентов rij. Без потери общности можно предположить, что эта матрица симметрична. Функция ошибок может быть записана в виде

 

   (2.12)

 

Так как [Uβ]' —β'U', a R — симметричная матрица, то

 

                      (2.13)

 

Дифференцирование этого выражения по р дает (см. приложение В)

 

           (2.14)

 

Последнее выражение можно записать в виде -2U'R[y-Uβ]= — 2U'Re.

При некотором р выражение (2.14) обращается в нуль. Отсюда находим р, обеспечивающее экстремум функции ошибок Е:

 

                                   (2.15)

 

Эту систему называют системой нормальных уравнений. Если U'RU — невырожденная матрица, то

 

                              (2.16)

 

Нетрудно показать, что при β = β^ функций ошибок Е принимает минимальное значение. Это значение Е (β^) называется остаточной ошибкой (основанной на k наблюдениях).

Здесь уместно сделать несколько замечаний:

1) Конечно, уравнение (2.16) можно решить методами

вариационного исчисления:

 

 

или

 

 

при произвольном ∆β (принцип ортогональности).

2) Прямое доказательство того, что Е достигает минимума, может быть основано на стандартном приеме анализа членов второго порядка по р. Из формулы (2.12) имеем

 

 

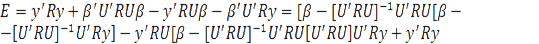
Очевидно, что при p, удовлетворяющем уравнению (2.16), Е достигает минимума.

3) В качестве мнемонического правила может оказаться удобным использовать то, что

 

 

умножается на U'R:

 

 

Так как второе слагаемое неизвестно, не измеряется и предполагается, что U и n статистически независимы, то это слагаемое отбрасывается. В результате получается оценка Р истинного значения b [см. формулу (2.15)]. Естественно, такой способ вывода уравнения (2.16) не показывает, в каком смысле оценка оптимальна.

Эта оценка обладает свойством линейности, поскольку

 

          (2.17)

 

Из формул (6.31) и (6.24) следует, что

 

 

Поскольку входной сигнал и шум статистически независимы,

 

                     (2.18)

 

А так как уже предполагалось, что ε[n] = 0, то оценка является и несмещенной:

 

Отсюда следует, что

 

т. е. математическое ожидание выхода модели равно выходу объекта без аддитивного шума.

Желательно определить еще одну характеристику оценки β [формула (2.16)] — ее дисперсию. Интересно также оценить корреляцию между компонентами вектора 3. Все эти характеристики можно определить с помощью ковариационной матрицы

 

    (2.19)

 

По-прежнему предполагается, что справедливо соотношение (6.24) и U и n статистически независимы. Тогда, используя формулу (6.32), находим

 

 (2.20)

 

Следовательно,

 

 

Будет показано, что в нескольких практически интересных случаях это выражение можно существенно упростить. Главная диагональ матрицы состоит из оценок дисперсий оцениваемых параметров.