 |
Главная |
Теорема о мгновенной оси вращения
|
из
5.00
|
 Перейдем к понятию мгновенной оси вращения. Рассмотрим сначала частный случай движения твердого тела. Пусть тело совершает плоскопараллельное движение, а пластинка S, скрепленная с телом, движется при этом в своей плоскости (рис.2.2). Пусть в данный момент времени t существует точка P пластинки, скорость которой в этот момент равна нулю:
Перейдем к понятию мгновенной оси вращения. Рассмотрим сначала частный случай движения твердого тела. Пусть тело совершает плоскопараллельное движение, а пластинка S, скрепленная с телом, движется при этом в своей плоскости (рис.2.2). Пусть в данный момент времени t существует точка P пластинки, скорость которой в этот момент равна нулю:  . Известно, что при непоступательном движении пластинки в любой момент времени существует единственная точка пластинки, скорость которой равна нулю в этот момент. Тогда в этот момент скорость любой точки тела, лежащей на прямой AB, проходящей через точку P перпендикулярно к пластинке S, тоже равна нулю. Следовательно, в этот момент существует прямая AB тела, скорость любой точки которой в этот момент равна нулю. В следующий момент времени t уже другая точка пластинки и соответственно другая прямая тела (перпендикулярная к S) обладает этим свойством.
. Известно, что при непоступательном движении пластинки в любой момент времени существует единственная точка пластинки, скорость которой равна нулю в этот момент. Тогда в этот момент скорость любой точки тела, лежащей на прямой AB, проходящей через точку P перпендикулярно к пластинке S, тоже равна нулю. Следовательно, в этот момент существует прямая AB тела, скорость любой точки которой в этот момент равна нулю. В следующий момент времени t уже другая точка пластинки и соответственно другая прямая тела (перпендикулярная к S) обладает этим свойством.
Определение. Подвижная прямая, совпадающая в данный
момент времени с той прямой тела, скорости всех точек которой в этот момент равны нулю, называется мгновенной осью вращения [3, 6].
Название «мгновенная ось вращения» будет понятным из дальнейшего. Поставим вопрос: при каких условиях для движущегося тела существует мгновенная ось вращения? Имеет место
Теорема. Если при непоступательном движении твердого тела в данный момент времени существует хотя бы одна точка O тела, скорость которой равна нулю, то в этот момент:
1) существует прямая тела, проходящая через точку O, такая, что скорости всех ее точек равны нулю;
2) существует единственный вектор  такой, что скорость любой точки A тела определяется соотношением
такой, что скорость любой точки A тела определяется соотношением  .
.

Доказательство. Пусть в данный момент времени t скорость точки O тела (рис.2.3) равна нулю:  . Возьмем в теле две точки A и B, для которых в этот момент
. Возьмем в теле две точки A и B, для которых в этот момент  ,
,  , и
, и  ∦
∦ 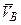 (согласно теореме о проекциях скоростей двух точек твердого тела такие точки обязательно найдутся, если не все точки тела имеют в данный момент нулевые скорости). Обозначим
(согласно теореме о проекциях скоростей двух точек твердого тела такие точки обязательно найдутся, если не все точки тела имеют в данный момент нулевые скорости). Обозначим 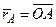 и
и  радиусы-векторы точек A и B.
радиусы-векторы точек A и B.
Проведем через точку A плоскость П1, перпендикуляр-ную к вектору  , через точку B – плоскость П2⊥
, через точку B – плоскость П2⊥  . Каждая из этих плоскостей проходит через точку O, так как из теоремы о проекциях следует, что
. Каждая из этих плоскостей проходит через точку O, так как из теоремы о проекциях следует, что  ⊥
⊥  ,
, 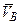 ⊥
⊥  . При этом для любой точки тела C, лежащей в плоскости П1, получаем, что
. При этом для любой точки тела C, лежащей в плоскости П1, получаем, что  ⊥П1 (или
⊥П1 (или  =0), так как
=0), так как 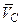 ⊥AC и
⊥AC и 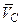 ⊥OC. Аналогично получаем, что вектор скорости любой точки D тела, лежащей в плоскости П2, перпендикулярен к плоскости П2 (или
⊥OC. Аналогично получаем, что вектор скорости любой точки D тела, лежащей в плоскости П2, перпендикулярен к плоскости П2 (или  =0). Отсюда следует, что скорость любой точки P тела, лежащей на линии пересечения плоскостей П1 и П2, равна нулю, так как вектор
=0). Отсюда следует, что скорость любой точки P тела, лежащей на линии пересечения плоскостей П1 и П2, равна нулю, так как вектор  не может быть перпендику-лярным одновременно к двум разным плоскостям П1 и П2. Доказано, что в данный момент времени в теле существует прямая OP, скорость любой точки которой равна нулю.
не может быть перпендику-лярным одновременно к двум разным плоскостям П1 и П2. Доказано, что в данный момент времени в теле существует прямая OP, скорость любой точки которой равна нулю.
Для доказательства второй части теоремы, учитывая, что  ⊥
⊥  , запишем (формально) соотношение
, запишем (формально) соотношение
 , (2.4)
, (2.4)
где  – неизвестный пока вектор. Из (2.4) следует, что вектор
– неизвестный пока вектор. Из (2.4) следует, что вектор  должен быть расположен как-то в плоскости П1. Будем искать такой вектор
должен быть расположен как-то в плоскости П1. Будем искать такой вектор  , чтобы формула (2.4) имела место для любой точки тела. В таком случае вектор
, чтобы формула (2.4) имела место для любой точки тела. В таком случае вектор  должен располагаться во всех плоскостях Пi одновременно, т.е. должен быть направлен по прямой OP. Учитывая это, можем для точки A тела определить по известным векторам
должен располагаться во всех плоскостях Пi одновременно, т.е. должен быть направлен по прямой OP. Учитывая это, можем для точки A тела определить по известным векторам  и
и  единственный вектор
единственный вектор  , направленный по OP. Обозначим его
, направленный по OP. Обозначим его  . Покажем, что при этом соотношение (2.4) с этим вектором
. Покажем, что при этом соотношение (2.4) с этим вектором  =
=  будет справедливо и для любой другой точки тела. Действительно, для точек O и P тела имеем тождественно:
будет справедливо и для любой другой точки тела. Действительно, для точек O и P тела имеем тождественно:  и
и  . Причем точки O, P, A не лежат на одной прямой. Но известно, что векторы скоростей трех точек тела, не лежащих на одной прямой, полностью определяют все распределение скоростей в теле, следовательно, этот вектор
. Причем точки O, P, A не лежат на одной прямой. Но известно, что векторы скоростей трех точек тела, не лежащих на одной прямой, полностью определяют все распределение скоростей в теле, следовательно, этот вектор  =
=  в соотношении (2.4) один и тот же для всех точек тела.
в соотношении (2.4) один и тот же для всех точек тела.
Итак, доказано существование единственного вектора  , направленного по прямой OP, такого, что для любой точки тела в данный момент справедливо:
, направленного по прямой OP, такого, что для любой точки тела в данный момент справедливо:  . Причем, как следует из (2.4),
. Причем, как следует из (2.4),  , т.е.
, т.е.
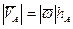 , (2.5)
, (2.5)
где hA – кратчайшее расстояние от точки до оси OP (рис.2.3). Теорема доказана.
Из теоремы следует:
1) в данный момент времени равны нулю скорости тех и только тех точек тела, которые лежат на прямой OP;
2) скорость каждой из остальных точек определяется в данный момент по формулам (2.4), (2.5).
Отметим, что формула, аналогичная формуле (2.4), определяет распределение скоростей и в частном случае – при вращении тела вокруг неподвижной оси.
Замечание 1. Если в данный момент времени в движу-щемся теле скорости точек, расположенных на одной прямой OP, равны нулю, а скорость любой другой точки отлична от нуля и удовлетворяет соотношению (2.4), то движение твердого тела называют мгновенно вращательным. Вектор  называют при этом вектором мгновенной угловой скорости тела, а подвижную прямую, совпадающую с прямой OP тела, – мгновенной осью вращения.
называют при этом вектором мгновенной угловой скорости тела, а подвижную прямую, совпадающую с прямой OP тела, – мгновенной осью вращения.
Название связано с тем, что распределение скоростей в таком теле полностью совпадает в данный момент времени с распределением скоростей в теле, вращающемся вокруг неподвижной оси. Но в отличие от последнего в рассматриваемом случае это распределение скоростей носит мгновенный характер, определяя поле скоростей лишь в данный момент, так как в следующий момент времени t1 мгновенная ось вращения (если она существует) и вектор 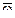 совпадают уже с другой прямой тела. При этом распределение ускорений отличается от распределения ускорений в теле, вращающемся вокруг неподвижной оси.
совпадают уже с другой прямой тела. При этом распределение ускорений отличается от распределения ускорений в теле, вращающемся вокруг неподвижной оси.
Кроме того, в рассматриваемом случае движение твердого тела за малый промежуток времени Dt, начиная от момента t, для которого справедливо соотношение (2.4), будет вращением вокруг прямой OP (с точностью до малых величин первого порядка малости включительно). Действительно, обозначим SA(t) дуговую координату точки A, определяющую ее положение на траектории в момент времени t, SA(t+Dt) - в момент времени t1= t+Dt. Будем рассматривать промежуток времени t1= t-Dt как малую величину первого порядка малости и разложим SA(t+Dt) в ряд Тейлора по степеням малой величины Dt:

или DSA= SA (t+Dt)- SA (t)=(VA)t Dt+(WAt)t (Dt)2/2+…
С точностью до малых величин первого порядка малости
DSA » (VA)t Dt.
Следовательно, если в момент времени t скорость точки A отлична от нуля, то перемещение точки A за промежуток времени Dt, определяемое величиной DSA, отлично от нуля. Если в момент t скорость точки O равна нулю, то с точностью до малых величин первого порядка малости включительно (т.е. пренебрегая малыми величинами, начиная со второго порядка малости), получим  .
.
Таким образом, можем считать точки прямой OP тела неподвижными в течение малого промежутка Dt, в то время как все остальные точки тела перемещаются. Следовательно, с указанной точностью движение тела за этот малый промежуток времени есть поворот на элементарный угол q вокруг прямой OP (рис.2.4).
 На рис.2.4 показаны положения точек тела в момент времени t - A, P, O и (с принятой точностью) в момент времени t1= t+Dt - A¢, P, O. При этом DSA » hAq.
На рис.2.4 показаны положения точек тела в момент времени t - A, P, O и (с принятой точностью) в момент времени t1= t+Dt - A¢, P, O. При этом DSA » hAq.
Замечание 2. Для произволь-ной точки A тела за малый промежуток времени Dt получаем DSA= hAq+..., где многоточие означает невыписанные члены не ниже второго порядка малости. Разделим это соотношение на Dt и перейдем к пределу при Dt®0:
 .
.
Из сравнения полученного равенства с формулой (2.5) следует, что при мгновенно вращательном движении тела мгновенная угловая скорость вращения тела
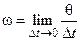
и не является производной по времени от какого-то конечного угла поворота тела в отличие от вращательного движения тела, когда ось вращения неподвижна.
Пример 2.1. Из изложенного следует, что если при непоступательном движении тела в данный момент времени существует хотя бы одна точка тела, скорость которой равна нулю, то существует и мгновенная ось вращения в данный момент. Если в этот момент известна скорость хотя бы одной точки тела, не лежащей на мгновенной оси вращения, то тем самым известно и все распределение скоростей в теле в этот момент. Действительно, можно сразу определить вектор 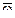 мгновенной угловой скорости тела, а затем формула (2.4) и определит скорость любой другой точки тела.
мгновенной угловой скорости тела, а затем формула (2.4) и определит скорость любой другой точки тела.
В качестве примера рассмотрим движение бегунка, устройство которого показано на рис.2.5.

Такие бегунки находят разнообразное техническое применение. Бегунок AB представляет собой колесо, свободно насаженное на горизонтальный вал OC (ось OZ). Вал OC приводится во вращение вокруг вертикального вала с осью O1Z1 с угловой скоростью  . Принимаем, что бегунок AB катится при этом без скольжения по горизонтальной плоскости. Последнее означает, что скорость точки A касания бегунка равна нулю VA=0. Следовательно, существует мгновенная ось вращения бегунка, проходящая в данный момент времени через точку A тела. Неподвижную точку O пересечения осей O1Z1 и OZ можно рассматривать также принадлежащей телу AB, и так как скорость ее в любой момент равна нулю, то мгновенная ось вращения бегунка в любой момент проходит через точку O.
. Принимаем, что бегунок AB катится при этом без скольжения по горизонтальной плоскости. Последнее означает, что скорость точки A касания бегунка равна нулю VA=0. Следовательно, существует мгновенная ось вращения бегунка, проходящая в данный момент времени через точку A тела. Неподвижную точку O пересечения осей O1Z1 и OZ можно рассматривать также принадлежащей телу AB, и так как скорость ее в любой момент равна нулю, то мгновенная ось вращения бегунка в любой момент проходит через точку O.
Таким образом, при движении бегунка в каждый момент
времени существует мгновенная ось вращения, проходящая через точку O и ту точку бегунка, которая в данный момент касается горизонтальной плоскости. На рис.2.5 – это прямая OA.
Определим величину мгновенной угловой скорости 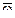 . С одной стороны, VC =whC, где hC – расстояние от точки C до мгновенной оси вращения, т.е. до прямой OA. С другой стороны, точка C, как точка горизонтального вала, имеет скорость VC=w1OC.
. С одной стороны, VC =whC, где hC – расстояние от точки C до мгновенной оси вращения, т.е. до прямой OA. С другой стороны, точка C, как точка горизонтального вала, имеет скорость VC=w1OC.
Следовательно, whC =w1OC, где hC = OCsina, и w=w1/sina.
В соответствии с принятым выше определением движение бегунка – мгновенно вращательное. Заметим, что при движении бегунка одна его точка O остается неподвижной. Такое движение тела называют еще сферическим.
 Пример 2.2. В качестве другого примера рассмотрим движение тела с одной неподвижной точкой (рис.2.6) (сферическое движение). Ско-рость точки O тела равна нулю, следовательно, сферическое дви-жение тела – это мгновенно вра-щательное движение. При этом, как следует из изложенного, существует мгновенная ось вращения OP,
Пример 2.2. В качестве другого примера рассмотрим движение тела с одной неподвижной точкой (рис.2.6) (сферическое движение). Ско-рость точки O тела равна нулю, следовательно, сферическое дви-жение тела – это мгновенно вра-щательное движение. При этом, как следует из изложенного, существует мгновенная ось вращения OP, 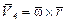 ,
,
 .
.
|
из
5.00
|
Обсуждение в статье: Теорема о мгновенной оси вращения |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

