 |
Главная |
Связь между абсолютной и относительной производными вектора по скалярному аргументу
|
из
5.00
|
В разд.1.1 (часть II) были введены понятия абсолютной и относительной производных вектора по скалярному аргументу. Найдем соотношение между этими производными. Сохраняя обозначения разд.1.1, дифференцируя по 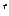 (1.6) и учитывая (1.10), получаем
(1.6) и учитывая (1.10), получаем
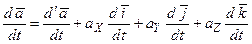 . (2.6)
. (2.6)
Отсюда следует, что в частном случае, когда подвижная система координат OXYZ (рис.1.3) движется поступательно (т.е. 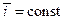 ,
, 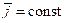 ,
, 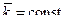 ), имеем
), имеем 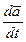 =
= 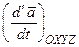 .
.
В общем случае (при непоступательном движении системы координат OXYZ ) 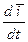 ≠ 0,
≠ 0, 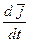 ≠ 0,
≠ 0, 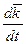 ≠ 0. Выясним, чему равны эти производные. Для этого введем в дополнение к системе координат рис.1.3 промежуточную подвижную систему координат Ozhx (рис.2.7), движущуюся поступательно.
≠ 0. Выясним, чему равны эти производные. Для этого введем в дополнение к системе координат рис.1.3 промежуточную подвижную систему координат Ozhx (рис.2.7), движущуюся поступательно.
По доказанному выше, 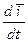 =
= 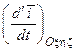 , причем
, причем 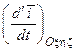 =
= 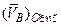 , где точка B, конец вектора
, где точка B, конец вектора 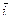 ,
,
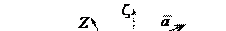 принадлежит системе OXYZ (рис.2.7). Заметим, что система OXYZ в своем движении по отношению к системе Ozhx имеет неподвижную точку O. Следовательно, по теореме о мгновенной оси вращения это движение – мгновенно вращательное и
принадлежит системе OXYZ (рис.2.7). Заметим, что система OXYZ в своем движении по отношению к системе Ozhx имеет неподвижную точку O. Следовательно, по теореме о мгновенной оси вращения это движение – мгновенно вращательное и
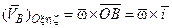 .
.
Здесь 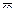 – мгновенная угло-вая скорость подвижной системы координат OXYZ. Итак,
– мгновенная угло-вая скорость подвижной системы координат OXYZ. Итак, 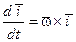 . Аналогично
. Аналогично 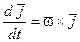 и
и 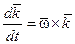 .
.
Подставляя это в (2.6), получаем
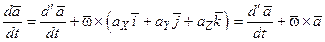 . (2.7)
. (2.7)
Соотношение (2.7) устанавливает теорему о связи между абсолютной и относительной производными вектора 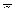 .
.
Теорема. Абсолютная производная вектора 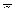 по скаляр-ному аргументу равна сумме относительной производной этого вектора, вычисленной по отношению к подвижной системе координат, и векторного произведения вектора
по скаляр-ному аргументу равна сумме относительной производной этого вектора, вычисленной по отношению к подвижной системе координат, и векторного произведения вектора 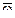 мгновенной угловой скорости этой подвижной системы на дифференцируемый вектор
мгновенной угловой скорости этой подвижной системы на дифференцируемый вектор 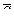 .
.
Теорема Кориолиса
Рассмотрим опять (как в гл.1 части II) сложное движение точки. Докажем теперь теорему о сложении ускорений в сложном движении точки. Будем использовать обозначения и терминологию, принятую выше.
Теорема. Абсолютное ускорение точки, совершающей сложное движение, равно геометрической сумме относительного, переносного и кориолисова ускорений: 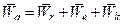 , где кориолисовым ускорением
, где кориолисовым ускорением 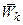 называют вектор, определяемый соотношением:
называют вектор, определяемый соотношением: 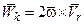 ,
, 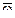 - угловая скорость подвижной системы координат (угловая скорость переносного движения,
- угловая скорость подвижной системы координат (угловая скорость переносного движения, 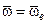 ).
).
 Доказательство. Пусть O1X1Y1Z1 – основная (неподвижная) система координат; OXYZ - подвижная система координат (рис.2.8); M - точка, совершающая сложное движение; m - точка системы координат OXYZ, с которой в момент t совпадает точка M. Введем дополнительно поступательно движущуюся систему коорди-нат Ozhx и обозначим
Доказательство. Пусть O1X1Y1Z1 – основная (неподвижная) система координат; OXYZ - подвижная система координат (рис.2.8); M - точка, совершающая сложное движение; m - точка системы координат OXYZ, с которой в момент t совпадает точка M. Введем дополнительно поступательно движущуюся систему коорди-нат Ozhx и обозначим 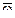 – вектор мгновенной угловой скорости подвижной системы координат OXYZ.
– вектор мгновенной угловой скорости подвижной системы координат OXYZ.
Найдем абсолютное ускорение точки M. По определению 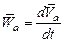 , где
, где 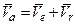 ,
, 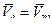 (по определению переносной скорости). Определим
(по определению переносной скорости). Определим 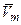 – абсолютную скорость точки m. Для этого будем рассматривать движение точки m по отношению к системе O1X1Y1Z1 как сложное, состоящее из двух составляющих движений, где 1) относительное движение точки m по отношению к системе Ozhx, 2) перенос-ное движение системы Ozhx по отношению к системе O1X1Y1Z1. Тогда по теореме о сложении скоростей получаем для точки
– абсолютную скорость точки m. Для этого будем рассматривать движение точки m по отношению к системе O1X1Y1Z1 как сложное, состоящее из двух составляющих движений, где 1) относительное движение точки m по отношению к системе Ozhx, 2) перенос-ное движение системы Ozhx по отношению к системе O1X1Y1Z1. Тогда по теореме о сложении скоростей получаем для точки 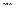 :
: 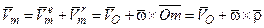 .
.
Следовательно, для точки M: 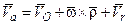 . Дифференцируя
. Дифференцируя 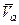 по t, имеем:
по t, имеем:
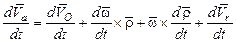 .
.
Здесь 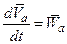 ;
; 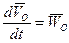 ;
; 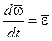 - вектор углового ускорения подвижной системы координат OXYZ; согласно (2.7):
- вектор углового ускорения подвижной системы координат OXYZ; согласно (2.7): 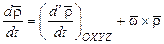 ,
, 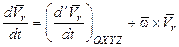 , причем
, причем 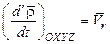 ;
; 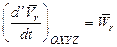 - по определению (разд.1.2, часть II). С учетом этого получаем:
- по определению (разд.1.2, часть II). С учетом этого получаем:
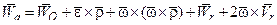 . (2.8)
. (2.8)
Заметим, что в этом соотношении сумма первых трех слагаемых определяет переносное ускорение точки M. Действительно, положим в (2.8) 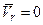 и
и 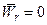 , т.е. жестко скрепим точку M с подвижной системой OXYZ. Тогда из (2.8) получим выражение для ускорения точки m, принадлежащей системе OXYZ, что и дает переносное ускорение точки M:
, т.е. жестко скрепим точку M с подвижной системой OXYZ. Тогда из (2.8) получим выражение для ускорения точки m, принадлежащей системе OXYZ, что и дает переносное ускорение точки M:
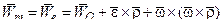 .
.
Итак, получим 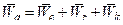 . Вектор
. Вектор 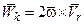 называют ускорением Кориолиса. Теорема доказана.
называют ускорением Кориолиса. Теорема доказана.
Глава3. Сложное движение твердого тела
Постановка задачи
 Будем рассматривать движение твердого тела T (рис.3.1) по отношению к двум различным системам координат O1X1Y1Z1 и OXYZ, которые движутся одна относительно другой.
Будем рассматривать движение твердого тела T (рис.3.1) по отношению к двум различным системам координат O1X1Y1Z1 и OXYZ, которые движутся одна относительно другой.
Поставим задачу: определить движение тела T по отношению к системе координат O1X1Y1Z1, если дано: 1) движение тела T по отношению к системе коор-динат OXYZ; 2) движение системы OXYZ по отношению к системе O1X1Y1Z1.
При такой постановке задачи движение тела T по отношению к системе O1X1Y1Z1 называют сложным (или составным), так как оно определяется через два промежуточных движения 1) и 2), которые при этом называют составляющими движениями. Определение (нахождение) движения тела T относительно системы координат O1X1Y1Z1 по составляющим движениям называют (как и в кинематике точки) сложением движений.
Очевидно, можно говорить и о разложении заданного движения тела на составляющие движения, понимая под этим, что движение тела по отношению к данной системе отсчета O1X1Y1Z1 можно рассматривать (вводя дополнительную систему OXYZ) как сложное, состоящее из двух составляющих движений: из движения тела по отношению к дополнительной системе отсчета OXYZ и из движения этой системы OXYZ по отношению к данной системе O1X1Y1Z1. Совершенно ясно, что задача разложения заданного движения тела на составляющие движения будет иметь разные решения для различных дополнительных систем отсчета.
В теории сложного движения тела принята терминология, аналогичная той, которая используется в теории сложного движения точки (см. гл.1). В соответствии с этим O1X1Y1Z1 – основная (неподвижная) система координат; OXYZ – подвижная система координат. Движение тела T по отношению к основной системе координат называют абсолютным, движение тела T по отношению к подвижной системе координат – относительным, движение системы координат по отношению к неподвижной системе координат – переносным. Кинематические элементы абсолютного движения тела T называются абсолютными и обозначаются индексом  ; кинематические элементы движения тела T в подвижной системе координат называются относительными и обозначаются индексом r; кинематические элементы движения подвижной системы координат OXYZ называются переносными и обозначаются e [3, 8].
; кинематические элементы движения тела T в подвижной системе координат называются относительными и обозначаются индексом r; кинематические элементы движения подвижной системы координат OXYZ называются переносными и обозначаются e [3, 8].
Используя терминологию теории сложного движения, сформулируем в общей постановке задачу сложения движений для твердого тела: по заданным относительному и переносному движениям, по движениям 1) и 2), найти абсолютное движение тела.
Замечание. Здесь используются понятия «движение тела» и «мгновенное движение тела». Подчеркнем, что последний термин (вообще говоря, неудачный, но традиционно исполь-зуемый [3]) является условным и характеризует лишь поле скоростей (распределение скоростей) в теле в данный момент.
Например, говорят:
движение тела в данной системе отсчета – мгновенно вра-щательное, если в данной момент в теле существует точка P, скорость которой равна нулю, а для любой другой точки A тела справедливо – 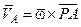 (где
(где 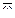 – вектор мгновенной, т.е. отвечающей этому моменту, угловой скорости, проходящей через точку P);
– вектор мгновенной, т.е. отвечающей этому моменту, угловой скорости, проходящей через точку P);
движение тела в данной системе отсчета – мгновенно поступательное, если в данный момент скорости всех точек тела по отношению к данной системе равны между собой – 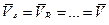 .
.
|
из
5.00
|
Обсуждение в статье: Связь между абсолютной и относительной производными вектора по скалярному аргументу |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

