 |
Главная |
Понятие о производной вектора по скалярному аргументу
|
из
5.00
|
Напомним некоторые известные понятия [2, 3, 4, 7, 10]. Пусть в системе координат OXYZ (рис. 1.1) задан переменный вектор
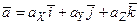 (1.1)
(1.1)
как непрерывная функция скалярного аргумента t, т.е. вектор-функция. Здесь aX = aX(t), aY = aY(t), aZ = aZ(t) - проекции вектора 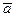 на оси OX, OY, OZ соответственно;
на оси OX, OY, OZ соответственно; 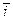 ,
, 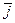 ,
,  - орты этих осей. Как известно [3, 10], производной вектор-функции
- орты этих осей. Как известно [3, 10], производной вектор-функции 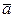 по скалярному аргументу t называют вектор, определяемый формулой
по скалярному аргументу t называют вектор, определяемый формулой
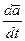 =
= 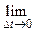
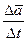 , (1.2)
, (1.2)
где 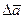 – приращение вектора
– приращение вектора 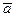 , соответствующее прираще-
, соответствующее прираще-
 |
нию аргумента Dt = t1-t в выбранной системе координат, т.е. 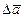 =
= 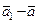 =
= 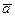 (t1)-
(t1)- 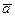 (t) или
(t) или
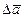 =[aX(t1) -aX(t)]
=[aX(t1) -aX(t)] 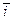 +[aY(t1) -aY(t)]
+[aY(t1) -aY(t)] 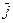 +[aZ(t1) -aZ(t)]
+[aZ(t1) -aZ(t)] 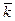 ;
;
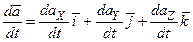 . (1.3)
. (1.3)
Направлен вектор 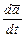 по касательной к годографу дифферен-
по касательной к годографу дифферен-
цируемого вектора 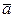 . Напомним также, что годографом вектор-функции
. Напомним также, что годографом вектор-функции 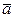 называют кривую, описываемую концом вектора
называют кривую, описываемую концом вектора 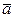 , начало которого перенесено в неподвижную в данной системе координат OXYZ точку (например, O), при непрерывном изменении скалярного аргумента t (рис.1.2).
, начало которого перенесено в неподвижную в данной системе координат OXYZ точку (например, O), при непрерывном изменении скалярного аргумента t (рис.1.2).
Уравнения годографа вектора 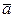 , заданного в системе координат OXYZ, имеют вид (в параметрической форме)
, заданного в системе координат OXYZ, имеют вид (в параметрической форме)
aX = aX(t), aY = aY(t), aZ = aZ(t). (1.4)
Из приведенных определений и формул (1.2) – (1.4) следует, что понятия производной вектор-функции по скаляр-ному аргументу и годографа вектора являются относитель-ными и необходимо всякий раз при использовании этих понятий четко указывать выбранную систему координат.
Будем рассматривать теперь две системы координат O1X1Y1Z1 и OXYZ, движущиеся одна относительно другой, и вектор-функцию 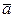 скалярного аргумента t, заданную в этих двух системах координат (рис.1.3). Пусть:
скалярного аргумента t, заданную в этих двух системах координат (рис.1.3). Пусть:
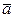 =
= 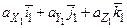 ; (1.5)
; (1.5)
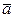 =
= 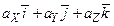 . (1.6)
. (1.6)
 Обозначения в формулах (1.5) и (1.6) имеют тот же смысл, что и в формуле (1.1). Далее для определенности будем полагать, что задано движе-ние системы координат OXYZ относительно системы O1X1Y1Z1. В таком случае систему координат O1X1Y1Z1 называют основной (или условно-неподвижной), а систему OXYZ - подвижной.
Обозначения в формулах (1.5) и (1.6) имеют тот же смысл, что и в формуле (1.1). Далее для определенности будем полагать, что задано движе-ние системы координат OXYZ относительно системы O1X1Y1Z1. В таком случае систему координат O1X1Y1Z1 называют основной (или условно-неподвижной), а систему OXYZ - подвижной.
Приращения вектора 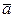 , соответствующие одному и тому же приращению аргумента Dt = t1-t, будут разными в разных системах координат. При этом приращение вектора
, соответствующие одному и тому же приращению аргумента Dt = t1-t, будут разными в разных системах координат. При этом приращение вектора 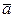 в неподвижной (основной) системе координат O1X1Y1Z1 называют абсолютным, обозначая его
в неподвижной (основной) системе координат O1X1Y1Z1 называют абсолютным, обозначая его 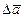 ; приращение вектора
; приращение вектора 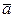 в подвижной системе координат – относительным, обозначая его
в подвижной системе координат – относительным, обозначая его 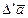 . Следовательно,
. Следовательно,
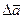 =
= 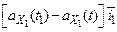 +
+ 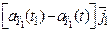 +
+ 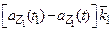 ; (1.7)
; (1.7)
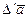 =
= 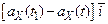 +
+ 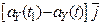 +
+ 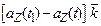 . (1.8)
. (1.8)
Соответственно этому называют производную вектор-функции 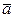 по скалярному аргументу в неподвижной системе координат O1X1Y1Z1 абсолютной, обозначая ее
по скалярному аргументу в неподвижной системе координат O1X1Y1Z1 абсолютной, обозначая ее 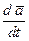 , а производную вектор-функции в подвижной системе координат OXYZ - относительной, обозначая ее
, а производную вектор-функции в подвижной системе координат OXYZ - относительной, обозначая ее 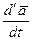 . Здесь в соответствии с соотношением (1.2):
. Здесь в соответствии с соотношением (1.2):
 ;
; 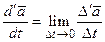 .
.
С учетом (1.7) и (1.8) получаем
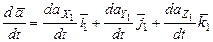 ; (1.9)
; (1.9)
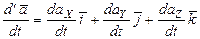 . (1.10)
. (1.10)
Заметим, что в общем случае 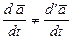 . Действительно,
. Действительно, 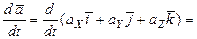
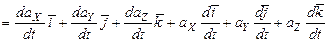 ,
,
где сумма первых трех слагаемых есть 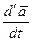 (по соотношению (1.10)), а последние три слагаемых отличны от нуля вследствие заданного движения системы координат OXYZ по отношению к системе O1X1Y1Z1, что и доказывает наше замечание. Заметим, что в некоторых учебниках и руководствах вместо обозначения
(по соотношению (1.10)), а последние три слагаемых отличны от нуля вследствие заданного движения системы координат OXYZ по отношению к системе O1X1Y1Z1, что и доказывает наше замечание. Заметим, что в некоторых учебниках и руководствах вместо обозначения 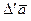 используют
используют 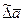 , относительную производную обозначают
, относительную производную обозначают 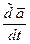 [3].
[3].
Аналогично будем называть кривую, описываемую в неподвижной системе координат O1X1Y1Z1 концом вектора 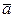 , начало которого перенесено в точку O1, абсолютным годографом вектора
, начало которого перенесено в точку O1, абсолютным годографом вектора 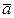 ; кривую, описываемую в подвижной системе координат OXYZ концом вектора
; кривую, описываемую в подвижной системе координат OXYZ концом вектора 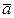 , начало которого перенесено в точку O, - относительным годографом вектора
, начало которого перенесено в точку O, - относительным годографом вектора 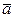 . Уравнения абсолютного годографа вектора
. Уравнения абсолютного годографа вектора 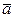 :
:
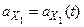 ;
; 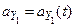 ;
; 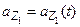 ;
;
уравнения относительного годографа вектора 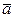 :
:
aX = aX (t), aY = aY (t), aZ = aZ (t).
|
из
5.00
|
Обсуждение в статье: Понятие о производной вектора по скалярному аргументу |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

