КАСКАДНОЕ СОЕДИНЕНИЕ ФИЛЬТРОВ

 

Если нужен фильтр с числом полюсов, большим двух, то его легко можно построить, соединив последовательно несколько фильтров более низкого порядка. В этом разделе объясняется, каким образом следует соединять активные фильтры для полу­чения многокаскадных фильтров более высоких порядков.

Соединяя каскадно фильтры первого и второго порядков, можно получить фильтр любого более высокого порядка.

 

 

Рис. 3.9.14. Каскадное соединение фильтров первого и второго порядков для получения фильтров более высоких порядков.

1 — фильтры первого порядка, 2 — фильтры второго порядка

 

Как видно из рис. 3.9.14, каскадное соединение фильтра второго по­рядка и фильтра первого порядка дает фильтр третьего по­рядка, а каскадное соединение двух фильтров второго порядка дает фильтр четвертого порядка. Увеличивая число соединяе­мых фильтров первого и второго порядков, можно получить фильтр любого нужного нам порядка. Фильтры нечетных поряд­ков обычно строятся из фильтра первого порядка в качестве первого каскада и нескольких фильтров второго порядка в качестве остальных каскадов. Например, фильтр седьмого порядка строится из одного (первого) каскада первого порядка и трех каскадов второго порядка. Фильтры четных порядков строятся из n/2 каскадов второго порядка, где n — желаемый порядок фильтра.

Ввиду того что каскадное соединение приводит к суже­нию полосы пропускания, отдельные каскады многокаскадных активных фильтров не следует делать идентичными.

Чтобы понять, как происходит сужение полосы пропускания,
рассмотрим рис. 3.9.15. Если каскадно соединить два фильтра
первого порядка с коэффициентами усиления К₁ и К₂ и с одинаковой полосой пропускания, то полоса пропускания полученного двухкаскадного фильтра окажется более узкой, чем полоса пропускания каждого из каскадов. Действительно, на частоте f₁ К₁ = 0,707 (K₁ в середине полосы) и К₂ = 0,707 (К₂ в середине полосы), поэтому на частоте f₁ общий коэффициент усиления К_Σ = К₁К₂ = 0,5 (К_Σ в середине полосы), т. е. меньше чем 0,707 (К_Σ в середине полосы). Аналогично на частоте f₂ К_Σ = 0,5 (К_Σ в середине полосы). Поэтому новое значение f'₁, при котором К_Σ = 0,707 (К_Σ в середине полосы), лежит
выше, чем f₁ а новое значение f'₂, при котором К_Σ = 0,707 (К_Σ в середине полосы), лежит ниже f₂, т. е. новая полоса пропу­скания оказывается уже старой. Если включить каскадно n идентичных фильтров первого порядка, то верхняя частота среза f'₂ и нижняя частота среза f'₁ n-каскадного фильтра будут связаны с верхней f₂ и нижней f₁ частотами среза каждого из каскадов соотношениями

 

f'₂ = f_{2 ,}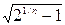

 

f'₁ = f_{21 .}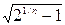

 

 

Рис. 3.9.15. Сужение полосы пропускания; f'₂ = 0,64f₂, f'₁ = l,55f₁

 

Эти соотношения относятся только к каскадам первого по­рядка, поэтому их нельзя использовать при расчете большин­ства многокаскадных активных фильтров, содержащих, как пра­вило, каскады второго порядка. Однако эффект сужения полосы пропускания при каскадном соединении фильтров имеет место независимо от порядка каскадов.

Неравномерность характеристики многокаскадного фильтра оказывается выше, чем неравномерность характеристики каж­дого из каскадов. Например, каскадное соединение двух фильтров второго порядка, имеющих каждый неравномерность харак­теристики 3 дБ, дает фильтр с неравномерностью 6 дБ, потому что К_Σ = К₁К₂ = K₁(дБ) + К₂(дБ).

Для получения наилучших результатов при конструировании многокаскадных фильтров оказывается необходимым использо­вать каскады с неодинаковыми значениями α и (если фильтр не является фильтром Баттерворта) f_ср. Так, три каскада второго порядка в фильтре шестого порядка могут иметь одну и ту же схему, но величины некоторых из компонентов должны быть различными для разных каскадов.

В многокаскадных полосовых фильтрах обычно используется четное число каскадов. Если ширина полосы пропускания по­лосового фильтра больше чем (приблизительно) 50 % f₀, то та­кой полосовой фильтр проще построить из фильтра верхних и фильтра нижних частот, соединив эти фильтры каскадно. По­строенный таким образом полосовой фильтр четвертого порядка, будет состоять из двух фильтров верхних частот второго по­рядка и из двух фильтров нижних частот второго порядка (рис. 3.9.16). Укажем, что в такой схеме фильтр нижних частот задает f₂, а фильтр верхних частот — f₁. Интервал частот, в котором полоса пропускания одного из этих фильтров перекры­вается с полосой другого, является полосой пропускания всей схемы.

Схемы каскадов первого порядка, которые используются при конструировании многокаскадных фильтров, показаны на рис. 3.9.17. Каждый из показанных на этом рисунке фильтров имеет α = 1. Отметим, что полосовой фильтр первого порядка — это скорректированный дифференциатор [2].

 

 

Рис. 3.9.16. Полосовой фильтр с широкой полосой, построенный

из фильтров верхних и нижних частот.

а — частотные характеристики; б — блок-схема полосового фильтра чет­вертого порядка; 1 — фильтры нижних частот второго порядка, 2 — фильтры верхних частот второго порядка

 

 

Рис. 3.9.17. Каскады первого порядка.

а – фильтр верхних частот, α = 1, f_СР = 1/2πRC ; б - фильтр нижних частот, α = 1, f_СР = 1/2πRC; в - полосовой фильтр, α = 1, f_СР = 1/2πRC, , f₂ = 1/2πR₂C₂, K_П = R₂/R₁

 

ВАРИАНТЫ ЗАДАНИЙ КУРСОВОЙ РАБОТЫ

 

(№ варианта соответствует порядковому номеру слушателя в учебном журнале на момент времени получения задания)

 

			Частоты среза АЧХ
№ варианта	Uвх,10-3В	Rвх,103Ом,не менее	Форма АЧХ	f1,Гц	f2,Гц	f3,кГц	f4,кГц	Ku,дБ в полосе пропускания	Rн, Ом	Рн, ВА	Uн, В	Режим работы транзисторов ОК УМ
1	2	3	4	5	6	7	8	9	10	11	12	13
0			Рис.4.1	130	1050	16
1	15	10	Рис.4.1	15	160	3,50		55	6			АВ
2	150	200	Рис.4.2	24	510	3,6			15		11	В
3		27	Рис.4.3	16	510	5,1	13	51	20	6		В
4	30	43	Рис.4.4	90	510	5,1		46	4			АВ
5	200	110	Рис.4.5	49	820	4,1	20		25		9	АВ
6		91	Рис.4.6	20	130	1,1	10,5	41	8	12		В
7	350	75	Рис.4.7	1800	5100	11		27	6			В
8	90	120	Рис.4.1	60	620	9,1			10		5	AB
9		15	Рис.4.2	120	1800	15		53	50	0,8		AB
10	80	51	Рис.4.3	27	750	6,8	17	42	16			АВ
11	150	220	Рис.4.4	10	50	0,62			28		9,5	АВ
12		47	Рис.4.5	23	710	2,9	11	47	18	7		В
13	300	160	Рис.4.6	10	82	610	6,2	32	16			АВ
14	70	15	Рис.4.7	1000	3100	7,1			6		8,5	В
15		56	Рис.4.1	100	1100	16		48	30	4		АВ
16	100	82	Рис.4.2	75	910	7,5		40	14			В
17	60	47	Рис.4.3	51	1200	10	27		5		8	В
18		68	Рис.4.4	20	220	2,2		46	20	2,5		AB
19	200	130	Рис.4.5	15	600	2,5	8,5	33	50			AB
20	80	51	Рис.4.6	33	240	2,1	22,5		16		10	АВ
21		16	Рис.4.7	3000	12000	25		26	30	3		AB
22	25	33	Рис.4.1	30	330	6,2		50	6			АВ
23	25	18	Рис.4.2	91	1200	9,1			25		9	АВ
24		100	Рис.4.3	21	620	5,6	15	35	15	6		АВ
25	120	150	Рис.4.4	15	70	0,75		38	8			В
26	40	62	Рис.4.5	36	760	3,5	16,5		16		9,5	АВ
27		51	Рис.4.6	24	180	1,65	15,5	49	12	9		АВ
28	450	22	Рис.4.7	1400	4300	18,1		23	10	5		АВ
29	50	82	Рис.4.1	80	820	12			16		7	AB
30		56	Рис.4.2	45	680	5,1		45	10	7		В

 

 

Рис.4.1. АЧХ вариантов № 0,1,8,15,22,29

Рис.4.2. АЧХ вариантов № 2,9,16,23,30

Рис.4.3. АЧХ вариантов № 3,10,17,24

 

Рис.4.4. АЧХ вариантов № 4,11,18,25

Рис.4.5. АЧХ вариантов №5,12,19,26

Рис.4.6. АЧХ вариантов № 6,13,20,27

 

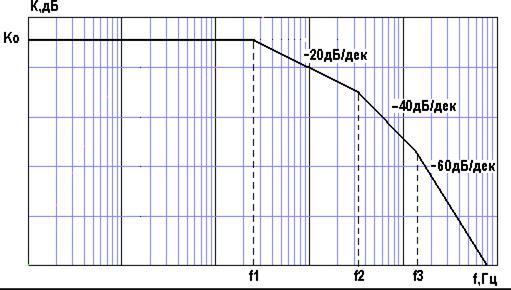
Рис.4.7. АЧХ вариантов № 7,14,21,28

 

 

СОДЕРЖАНИЕ И ПРАВИЛА ОФОРМЛЕНИЯ КУРСОВОЙ РАБОТЫ

СОДЕРЖАНИЕ ПОЯСНИТЕЛЬНОЙ ЗАПИСКИ И ГРАФИЧЕСКОЙ ЧАСТИ КУРСОВОГО ПРОЕКТА ПО ДИСЦИПЛИНЕ «ОСНОВЫ СХЕМОТЕХНИКИ»

I. Пояснительная записка содержит следующие разделы:

1. обзор электронных устройств (ЭУ) данного класса по литературным источникам;

2. анализ технического задания и синтез структурной и функциональной схем ЭУ;

3. разработка принципиальной схемы ЭУ;

4. электрический расчет ЭУ;

5. приложения;

6. список литературы.

Средний объем записки 25-35 страниц. ВАХ, нагрузочные прямые, спецификации, рисунки, встречающиеся в тексте, рисуются на миллиметровой бумаге и входят в состав раздела 5.

 

II. Графическая часть включает следующие чертежи:

1. чертеж структурной схемы (А3);

2. чертеж функциональной схемы (А3);

3. схема электрическая принципиальная (А3).