ДРУГИЕ ТИПЫ ЧАСТОТНЫХ ХАРАКТЕРИСТИК

Из всех известных типов фильтров в этой главе рассматри­ваются лишь фильтры Бесселя, Баттерворта и Чебышева. Су­ществуют и другие типы фильтров, в частности обратный фильтр Чебышева, характеристика которого равномерна в по­лосе пропускания, но имеет зубцы в полосе подавления; эллиптический фильтр с характеристикой, имеющей очень крутой наклон на переходном участке, но неравномерной и в полосе про­пускания, и в полосе подавления; параболический фильтр, обла­дающий очень хорошей импульсной характеристикой.

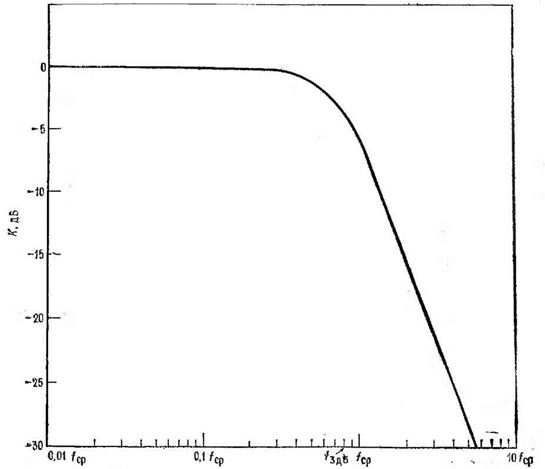
Рис. 3.9.4. Частотные характеристики фильтра нижних частот Бесселя второго порядка.

Наклон на переходном участке менее 6 дБ/октава на один полюс

НЕКОТОРЫЕ ОПРЕДЕЛЕНИЯ

Коэффициент затухания α определяет форму характеристики на переходном участке и вид выброса характеристики в полосе пропускания вблизи переходного участка. Таким образом, коэф­фициент затухания определяет форму частотной характеристики фильтра, т. е. его тип. Так, фильтр Баттерворта второго порядка имеет коэффициент затухания α, равный 1,414, а фильтр Чебы­шева второго порядка с неравномерностью 3 дБ имеет α = 0,766.

Одна и та же схема в зависимости от выбора значений ее компонентов может действовать как фильтр Бесселя, фильтр Баттерворта или фильтр Чебышева, и форма частотной характе­ристики фильтра определяется коэффициентом затухания. На рис. 3.9.5 показано несколько характеристик фильтров нижних частот при различных значениях коэффициента затухания.

Добротность Q связывает среднюю частоту полосы пропу­скания и ее ширину на уровне 3 дБ; рис. 3.9.6 иллюстрирует эту связь. Численно добротность равна

Q = f₀/(f₂ – f₁) = 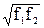/(f₂ – f₁).

f₀ = 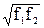— средняя частота, f₁ — нижняя частота среза на уровне 3 дБ, f₂ — верхняя частота среза на уровне 3 дБ. Для активных фильтров Q= 1/α.

Коэффициент усиления в полосе пропускания К_п активного фильтра равен отношению выходного напряжения к входному:

К_п = U_вых/U_вх.

Рис. 3.9.5. Частотные характеристики фильтров нижних частот при различных значениях коэффициента затухания.

1 — α = 1,732, фильтр Бесселя; 2 — α =1,414, фильтр Баттерворта; 3 — фильтр Чебышева с неравномерностью 1 дБ; 4 — фильтр Чебышева с неравномерностью 3 дБ.

Чувствительностью S одного из параметров фильтра по от­ношению к другому его параметру называется отношение вели­чины изменения первого параметра к величине изменения вто­рого, если изменение второго параметра вызвало изменение пер­вого. Например, равенство

 = - 0,5,

где ω₀ = 2πf₀, a R₁ — сопротивление резистора в схеме актив­ного фильтра, показывает, что ω₀ уменьшается на 0,5%, если R₁ увеличивается на 1 %.

Часто приходится рассчитывать чувствительность таких па­раметров полосовых фильтров, как f_cp, ω₀, α и Q. Соответствую­щие вычисления утомительны и требуют больших затрат времени, но их приходится выполнять, если предполагается исполь­зовать фильтр в широком диапазоне внешних температур или если параметры компонентов фильтра имеют большой разброс. Выражения для S имеют разный вид для различных типов фильтров; они приведены в некоторых книгах, указанных в конце пособия.

Рис. 3.9.6. Частотные характеристика полосовых фильтров.