Тема 1. Предмет логики

Введение

Трудно переоценить значение логики и теории аргументации не только в развитии научного знания, но и в обыденной жизни. Для науки существенным моментом являются эффективные способы обработки информации и методы исследования, формы мысли и операции с ними, основы доказательства, правила построения гипотезы и теории. В общем, всё то, что составляет основу логики и теории аргументации. В обыденной жизни очень важно уметь отстаивать свою точку зрения, находить выход из сложной жизненной ситуации. Этому во многом способствует изучение логики и теории аргументации.

Данная дисциплина сформировалась на стыке нескольких наук – логики, риторики, психологии и т.д. Причём теория аргументации и логика могут изучаться как отдельные дисциплины, каждая из которых имеет свою область исследования: логика – формы мышления, их особенности и взаимодействие, законы мышления; теория аргументации – способы убеждения. Объединение логики и теории аргументации преследует цель формирования логической культуры студента, основываясь на теоретическом знании основ логики и практического применения этих основ в процессе аргументации.

Развитое логическое мышление является одним из признаков современного образованного человека. Способность чётко мыслить, быстро принимать правильное решение на основании анализа сложившейся ситуации обеспечивает человеку востребованность и успешность в профессиональной деятельности. Например, умение использовать весь арсенал логических знаний и способов убеждения пригодится в профессиональной деятельности, предполагающей взаимодействие с людьми, возможность повлиять на их мнение, вкусы, выбор того или иного товара. Поэтому людям, выбравшим такую сферу деятельности, как например, связи с общественностью, управление персоналом и т.п. необходимо изучение логики и теории аргументации.

 

Тема 1. Предмет логики

Изучив материалы темы, Вы сможете:

- дать определение логики;

- охарактеризовать этапы развития формальной логики;

- указать особенности неклассической логики;

- понять смысл построения логических формализованных систем;

- назвать основные аспекты языка;

- уяснить своеобразие логического подхода к изучению мышления по сравнению с другими науками.

Логика – это наука о формах, методах и средствах правильного мышления. К общезначимым формам мысли относятся понятия, суждения, умозаключения, а к общезначимым средствам мысли – определения, правила образования понятий, суждений и умозаключений, правила перехода от одних суждений или умозаключениям к другим как следствиям из первых (правила рассуждений).

Формальная логика в своем развитии прошла два основных этапа. Начало первого этапа связано с работами древнегреческого философа Аристотеля, в которых впервые дано систематическое изложение логики. Логику Аристотеля и всю доматематическую логику обычно называют «традиционной» логикой. Традиционная логика выделяет и описывает зафиксированные в языке некоторые простейшие формы рассуждений. Второй этап – это появление математической или символической логики. Впервые в истории идеи о построении логики на математической основе были высказаны немецким математиком Г. Лейбницем в конце XVII в. Первая реализация идеи Лейбница принадлежит английскому ученому Д. Булю (середина XIX в.). Он создал алгебру, в которой буквами обозначены высказывания. Благодаря введению символов в логику была получена основа для создания новой науки – математической логики. Применение математики к логике позволило представить логические теории в новой удобной форме и применить вычислительный аппарат к решению задач, малодоступных человеческому мышлению в виду их сложности.

Современная символическая логика представляет собою весьма разветвленную область знания. Символическая логика подразделяется на классическую и неклассическую. Неклассическая же логика подразделяется также на интуиционистскую логику, модальную логику, логику вопросов, релевантную логику и др. В основе неклассической логики лежит представление о неприменимости в некоторых случаях закона исключённого третьего, в частности, когда речь идёт о бесконечных множествах. Кроме того, в ряде направлений неклассической логики изначально двухзначная логика Аристотеля трансформируется в трёхзначную, четырёхзначную, а затем в многозначную.

Традиционная логика имела эмпирический характер. Она выделяла и описывала зафиксированные в языке повседневного обихода некоторые простейшие формы рассуждений из так называемых категорических суждений. Современная логика расширила круг рассматриваемых форм, введя в него рассуждения, специфичные для научного познания, в частности, – математического. Более того, современная логика определила принципы теоретического обоснования условий правильности выводов и доказательств, используя понятия: логический закон и логическое следование.

В отличие от других наук, изучающих мышление, логика изучает особенности, свойства форм мысли, отвлекаясь при этом от того конкретного содержания, которое могут нести эти формы мысли; она изучает их со стороны строения, структуры, т.е. внутренней закономерной связи составляющих форму мысли элементов.

Следует иметь в виду, что логические формы и законы носят всеобщий и объективный характер, то есть они не связаны с какими-либо психофизиологическими особенностями людей или с теми или иными культурно-историческими факторами.

Мышление тесно связано с языком, однако, это не тождественные понятия. Язык – это материальное образование, представляющее собой определенную знаковую систему, позволяющую выражать мысли, хранить их и передавать. Мышление же – система идеальная. Если основные элементы языка – буквы, слова, словосочетания и предложения, то элементами мышления выступают отдельные формы мысли (понятия, суждения, умозаключения) и их сочетания.

Естественный язык представляет собой систему знаков. При рассмотрении языка как системы знаков важно принимать во внимание три основных аспекта языка: синтаксис, семантику и прагматику.

Синтаксический аспект включает многообразие отношений знаков к другим знакам, имеющиеся в языке правила образования одних знаков из других и правила изменения знаков.

Семантический аспект составляет совокупность отношений знаков к объектам внеязыковой действительности, то есть к тому, что они обозначают.

Прагматический аспект включает все такие особенности языка, которые зависят от того, кем и в каких ситуациях он применяется.

Исходя из принципа объективности знания, в науке стремятся исключить при определении смысловых содержаний языковых выражений и при описании познавательных процедур всякие возможные влияния субъективных особенностей познающих людей. Не должно быть, например, неопределённостей, двусмысленностей в выражении мысли в языке. Этим требованиям удовлетворяют специально построенные логические формализованные языки.

Основная цель логики – выяснение условий истинности знания и выработка эффективных познавательных процедур. Знание логики повышает культуру мышления, способствует четкости, последовательности и доказательности рассуждения, усиливает эффективность и убедительность речи. Логическая культура – это не врожденное качество. Логическая культура формируется в результате внимательного изучения логики и накопления опыта в практическом применении логических знаний.

Большое значение логика имеет в развитие и организации информационного процесса. Несоблюдение логической формы и логического следования в информационных процессах чревато негативными последствиями в различных сферах жизни человека и общества.

Контрольные вопросы:

1. Дайте определение логики как науки.

2. В чём отличие между традиционной логикой и символической?

3. Кто является основателем логики?

4. Какие основные аспекты языка Вы знаете?

5. Какие принципы составляют основу неклассической логики?

6. Какое практическое значение имеет изучение логики?

7. Назовите основные формы мысли.

Тема 2. Понятие

Изучив материалы темы, Вы сможете:

- уяснить логические приёмы образования понятий;

- дать логическую характеристику любому понятию, опираясь на классификацию понятий;

- определить отношения между понятиями по объёму;

- понять суть таких логических действий над понятиями, как обобщение, ограничение, деление и определение;

- назвать логические ошибки, возникающие при нарушении правил деления и определения.

- уяснить смысл операций с классами.

 

Понятие есть форма мысли, отражающая общие, существенные и специфические признаки предметов, явлений, процессов.

Формирование понятие возможно путём применения таких логических приёмов, как анализ, синтез, абстрагирование, обобщение. Анализ – мысленное расчленение предметов на их составные части, мысленное выделение в них признаков (т. е. свойств и отношений). Синтез – мысленное соединение в единое целое частей предмета или его признаков, полученных в процессе анализа, которое осуществляется как в практической деятельности, так и в процессе познания. Абстрагирование – мысленное выделение, вычленение отдельных интересующих нас признаков, свойств, связей и отношений конкретного предмета или явления и мысленное отвлечение их от множества других признаков, свойств, связей и отношений этого предмета. Обобщение – мысленное выделение каких-нибудь свойств, принадлежащих некоторому классу предметов; переход от единичного к общему, от менее общего к более общему.

Знакомясь с учением о понятии, важно четко уяснить, что понятие как мысль не тождественно ни слову его выражающему, ни предмету, который оно отражает.

Понятие имеет только два элемента своей структуры - содержаниеи объем. Объем – это множество предметов мысли, объединенных в понятии. Содержание – множество признаков предметов, объединенных в понятии. Существует следующее отношение между объёмом и содержанием понятия: чем больше объём, тем меньше содержание; Чем меньше объём, тем больше содержание.

Выделение элементов структуры понятия и знакомство с их особенностями, свойствами дает возможность рассмотреть виды понятий, отношения между ними и, наконец, операции над понятиями.

По количеству понятия делятся на общие, единичные и «пустые». Общими называются понятия, объём которых содержит два и более элемента. Например, понятие «книга». Единичными называются понятия, объём которых содержит только один элемент. Например, понятие «Русский музей». По сути, все имена собственные являются единичными понятиями. Пустыми понятиями называются понятия, объём которых не содержит ни одного элемента. Например, понятие «кощей бессмертный» или понятие «квадратный круг».

По качеству понятия делятся на положительные, отрицательные, конкретные, абстрактные, соотносительные и безотносительные, сравнимые, несравнимые, собирательные и разделительные, регистрирующие, нерегистрирующие.

Положительные понятия – это понятия, которые указывают на наличие у предмета того или иного качества или отношения. Например, понятие «порядочность». Отрицательные понятия – это понятия, которые указывают на отсутствие у предмета некоторого качества или отношения. Например, понятие «бесполезность».

Конкретные понятия – это понятия, которые отражают предметы. Например, понятие «дом». Абстрактные понятия – это понятия, которые отражают свойства и отношения между предметами. Например, понятие «высота».

Собирательные понятия – это понятия, признаки которых относятся не к каждому элементу множества, а ко всему множеству в целом. Например, понятие «взвод». Разделительные понятия – это понятия, признаки которых относятся к каждому элементу множества предметов. Например, понятие «солдат».

Соотносительное понятие – это понятие, содержание которого представляет собой наличие или отсутствие отношения мыслимого в нём предмета к некоему другому предмету. В соотносительном понятии мыслится предмет, обусловливающий существование другого предмета. Например, понятие «начальник» обусловливает существование понятия «подчинённый». Безотносительное понятие – это понятие, содержание которого не связано каким-либо отношением, где мыслимые предметы (признаки) существуют вполне самостоятельно, независимо от других предметов (свойств). Например, понятие «карандаш».

Сравнимые понятия – это понятия, связь по содержанию между которыми близка. Например, понятие «человек» и понятие «живое существо». Несравнимые понятия – это понятия, связь по содержанию между которыми далека. Например, понятия «картина» и «крот» – несравнимые понятия.

Регистрирующими называются понятия, в которых множество мыслимых в нем элементов поддается учету, регистрируется (во всяком случае, в принципе). Например, «герои Советского Союза», «месяц». Регистрирующие понятия имеют конечный объем. Нерегистрирующими называются понятия, относящиеся к неопределенному числу элементов. Так, в понятиях «машина», «бумага» множество мыслимых в них элементов не поддается учету: в них мыслятся все люди, все кошки. Нерегистрирующие понятия имеют бесконечный объем.

Отношения между понятиями есть отношения между видами понятий. Отношения между понятиями бывают совместимыми и несовместимыми.

Совместимые понятия – это понятия, объёмы которых частично или полностью совпадают. Отношения совместимости: тождество, подчинение, пересечение. Тождественные понятия – это понятия, объёмы которых полностью совпадают. Подчиненные понятия – это понятия, объёмы которых имеют такое отношение, что объём одного из понятий полностью входит в объём другого, но не совпадает с ним. Подчиненные понятия отражают родовидовые отношения. Перекрещивающиеся (находящиеся в отношении пересечения) понятия – это понятия, объёмы которых частично совпадают.

Несовместимые понятия – это понятия, объёмы которых не имеют общих элементов. Отношения несовместимости: противоречие, противоположность, соподчинение. Соподчинённые понятия – это понятия, объёмы которых исключают друг друга, но одновременно входят в объём некоторого более широкого (родового) понятия. Противоречащие понятия – это понятия, которые являются видами некоторого рода, признаки которых взаимоисключают друг друга, а сумма их объёмов исчерпывает объём родового понятия. Противоположные понятия – это понятия, входящие в объём некоторого родового понятия и объёмы которых исключают друг друга. Объёмы противоположных понятий в своей совокупности не исчерпывают объёма родового понятия.

Для лучшего запоминания и ориентации в этих отношениях принято изображать все виды отношений при помощи кругов Эйлера:

 

тождество пересечение подчинение

 

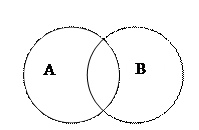
A –столица Франции A – спортсмен A – наука

B – Париж B – военный B – география

противоречие противоположность соподчинение

 

 

A – яблоко A – отличник A – мебель

не A – не яблоко B – двоечник B – шкаф

C – табуретка

 

Необходимо обратить внимание на то, что понятия близкие по содержанию не всегда соотносимы по объему. Например, понятия «кошка» и «хвост» связаны по содержанию, так как у кошки есть хвост, но объёмы этих понятий не имеют общих элементов (кошка не может быть хвостом, а хвост не может быть кошкой).

Кроме того, важно помнить, что единичное понятие не может находиться в отношении пересечения с другими понятиями в силу того, что данное понятие отражает множество, содержащее только один элемент.

Операции над понятиями наиболее сложная часть учения о понятии. Они представляют собой определенные преобразования исходных понятий. К операциям над понятиями относятся: обобщение, ограничение, деление, определение.

Операции обобщенияи ограничениясвязаны с отношением обратной зависимости содержания и объема. При обобщении осуществляется переход от понятия с меньшим объемом к понятию с большим объемом при сопутствующем этому процессу уменьшении содержания. Например, «Исаакиевский собор» – «собор» – «церковь». При ограничении происходит переход от понятия с большим объемом к понятию с меньшим объемом при сопутствующем этому процессу увеличении содержания. Например, «водоём» – «озеро» – «озеро Байкал».

Определение – это операция раскрывающая содержание понятия путем перечисления его родовых и видовых признаков. Определение включает в себя два элемента: определяемое и определяющее. Определяемое – это понятие, содержание которого следует раскрыть. Определяющее – это родовой и видовой признаки, за счёт которых раскрывается содержание определяемого. Например, «Квадрат – это прямоугольник, у которого все стороны равны». Квадрат – это определяемое, прямоугольник, у которого все стороны равны – это определяющее, причём прямоугольник – это ближайшее родовое понятие, а равенство всех сторон – видовой признак.

При определении следует соблюдать несколько правил, помогающих избежать ошибок в этой мыслительной операции.

Правила определения:

1. Определение должно быть соразмерным, то есть объём определяемого понятия должен быть равен объёму определяющего.

Например: «Дом – это строение». В данном случае определяющее больше чем определяемое, так как указан только родовой признак. Это определение слишком широкое.

Возможен вариант, когда имеет место слишком узкое определение. Например: «Музей – учреждение, изучающее предметы материальной культуры». Это определение исключает изучение предметов духовной культуры.

2. Определение не должно быть отрицательным.

Например: «Стул – это не стол». Из этого определения совершенно непонятно что такое стул и чем он отличается от стола.

3. Определение не должно содержать логического круга, то есть определяющее не должно раскрываться через определяемое.

Например: «Нумизмат – это человек, занимающийся нумизматикой».

4. Определение должно быть чётким, ясным, не должно содержать сравнений.

Например: «Лень – мать всех пороков». Это определение не раскрывает содержание определяемого понятия.

Кроме уже рассмотренного вида определения через ближайший род и видовое отличие, существуют другие виды определения, которые не столь популярны. Например, реальное и номинальное определения. Реальное определение – определение, в ходе которого реальный или абстрактный предмет выделяется из группы других предметов по некоторым отличительным признакам. Например: «Бриллиант есть отшлифованный алмаз». Нетрудно заметить, что все относящееся к определению через ближайший род и видовое отличие справедливо и для реального определения. Номинальное определение – определение, с помощью которого формулируется значение некоторого знакового выражения (термина). Например: «Бриллиантом называют отшлифованный алмаз». Ещё один вид определения – остенсивное определение. Остенсивное определение – определение значения слов или словосочетаний, соответствующих тем или иным предметам, свойствам, отношениям, действиям и т. п. путём их непосредственного показа. Чаще всего используется при обучении языку. Например, когда пытаются объяснить понятие «круглый» показывают круглый предмет: мяч, апельсин и т.д.

Деление – это логическая операция раскрывающая объем делимого понятия путем перечисления его видов. Деление состоит из трёх элементов: делимое, основание деления, члены деления. Делимое – это понятие, объём которого требуется разделить. Основание деления – это признак, по которому делят объём делимого понятия. Члены деления – это понятия, которые образуются в результате деления. Например, нам нужно провести операцию деления над понятием «велосипед», которое выступает в качестве делимого. Выбираем основание деления: количество колёс. В качестве членов деления получаем понятия: «духколёсный», «трёхколёсный», «четырёхколёсный». Существуют следующие виды деления: дихотомическое, деление по видоизменению признака и классификация. Деление дихотомическое – деление, при котором объём делимого понятия распределяется на два противоречащих друг другу класса. Например, понятие «карандаш» по цвету грифеля делится на «цветной» и «не цветной». Деление по видоизменению признака – деление, при котором выбранное основание деления является видообразующим признаком. Например, понятие «юбка» по длине делится на «длинную», «короткую», «средней длины». Классификация – логическая операция, при которой проводится многоступенчатое, разветвлённое деление объёма некоторого понятия, где каждая выделенная группа элементов имеет своё постоянное, вполне определённое место. Любая наука использует классификацию для упорядочивания объектов исследуемой области. В качестве примера классификации можно также указать расписание занятий, расписание поездов и т.д.

Правила деления:

1. Деление должно быть соразмерным, то есть сумма объёмов членов деления должна быть равна объёму делимого.

Например, если мы делим понятие «студенты» и получаем в качестве членов деления понятия «отличники» и «двоечники», то сумма объёмов членов деления меньше объёма делимого. Если же мы при делении понятия «студенты» получаем в качестве членов деления понятия «отличники», «хорошисты», «троечники», «двоечники» и «люди», то снова получаем несоразмерное деление. Понятие «люди» не входит в объём понятия «студенты».

2. Деление должно быть последовательным.

Например: «Студенты делятся на отличников, хорошистов, двоечников и старост». Скачок в делении возник из-за того, что не закончив делить родовое понятие «студенты», мы перешли к делению видового понятия «отличники».

3. Деление должно проводится только по одному основанию.

Например, «Студенты делятся на отличников, хорошистов и студентов вечернего отделения» – здесь, начав делить студентов по успеваемости, мы перескочили на форму обучения.

4. Члены деления должны находится в отношении соподчинения.

Например: «Студенты делятся на отличников, хорошистов, двоечников, троечников, принимающих участие в КВН, победителей олимпиады». Здесь члены деления не исключают друг друга: отличники, как, впрочем, и хорошисты могут быть победителями олимпиады, а участниками КВН могут быть и отличники, и хорошисты, и троечники.

Кроме вышеуказанных операций над понятием, существуют ещё операции с классами. Классом или множеством, называется определённая совокупность предметов (элементов класса), имеющих некоторые общие признаки.

Логические операции с классами: объединение классов (сложение), вычитание классов, пересечение классов (умножение) и образование дополнения к классу (отрицание) – применяются для образования из двух или нескольких классов новых классов. В операциях с классами приняты следующие обозначения: A, B, C… – произвольные классы, 1 – универсальный класс, 0 – нулевой (пустой) класс, – знак объединения классов (сложение), ∩ – знак пересечения классов (умножение), знаком Ā (не-А) обозначается дополнение к классу A (отрицание).

В операциях с классами используются круговые схемы, универсальный класс обозначается прямоугольником.

Операция объединения классов (сложение) состоит в объединении двух или нескольких классов в один класс, состоящий из элементов слагаемых классов. Операция записывается с помощью знака сложения: A B. Множество, полученное в результате сложения называется суммой. Например, объединим класс «шахматисты (A)» и класс «преподаватели (B)», приведём схему и символическую запись данной операции.

 

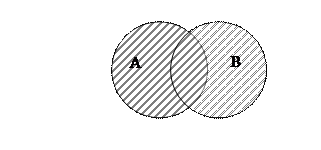
A B: результат сложения (сумма) включает шахматистов и преподавателей, а также преподавателей и шахматистов одновременно.

В результате операции вычитания классов образуется класс, состоящий из элементов, исключающих элементы вычитаемого класса. Множество, полученное в результате вычитания классов, называется разностью. Например, проведём операцию вычитания из класса «юрист (A)» класса «адвокат (В)» и приведём схему данной операции.

Результат вычитания (разность) – все юристы, кроме адвокатов.

Операция пересечения классов (умножение) состоит в отыскании элементов, общих для двух или нескольких классов. Операция записывается с помощью знака умножения: A∩B. Множество, полученное в результате умножения, называется произведением. Например, проведём операцию пересечения класса «врачи (А)» и класса «военные (В)», приведём символическую запись и схему данной операции.

А∩В: результат умножения (произведение) включает врачей, которые являются военными (область, где штриховка образует сетчатый узор)

Образование дополнения (отрицание). Дополнением к классу A называется класс не-A (Ā), который при сложении с A образует универсальную область. Эта область представляет собой универсальный класс и обозначается знаком 1. Чтобы образовать дополнение, нужно класс A исключить из универсального класса: 1- A =Ā. Образование дополнения состоит, таким образом, в образовании нового множества путём исключения данного множества из универсального класса, в который оно входит. Например, образуем дополнение к классу «студенты (1)», используя класс «студенты московских вузов (А)». Приведём символическую запись и схему.

1-А= Ā: результатом дополнения к классу студентов будут все студенты, кроме студентов московских вузов.

 

Контрольные вопросы:

1. Какие способы формирования понятия Вы знаете?

2. В чём разница между собирательными понятиями и разделительными?

3. Что такое «пустые» понятия?

4. В каком отношении находятся понятия «человек, знающий европейские языки» и «переводчик»?

5. Какие виды деления Вы знаете?

6. Какое понятие будет предельным при операции ограничение?

7. В чём отличие между реальным и номинальным определением?

8. Какой смысл заключается в операции дополнения?