 |
Главная |
Первое действие первого шага
|
из
5.00
|
Выбираем, как указано выше:  ,
,  . На первом шаге
. На первом шаге  — единичная матрица, так как базисными переменными являются
— единичная матрица, так как базисными переменными являются  , а свободными переменными являются
, а свободными переменными являются 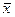 ,
,  по тем же причинам. Присвоим всем свободным переменным
по тем же причинам. Присвоим всем свободным переменным 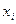 нулевые значения, и начнём движение от вершины
нулевые значения, и начнём движение от вершины  .
.
Второе действие очередного шага.
Покажем, что в выражении

только свободные переменные имеют ненулевой коэффициент. Заметим, что из выражения  базисные переменные однозначно выражаются через свободные, так как число базисных переменных равно числу уравнений. Уравнение
базисные переменные однозначно выражаются через свободные, так как число базисных переменных равно числу уравнений. Уравнение  можно переписать, как
можно переписать, как  . Умножим его на
. Умножим его на  слева:
слева:  . Таким образом, мы выразили базисные переменные через свободные, и в выражении
. Таким образом, мы выразили базисные переменные через свободные, и в выражении  , эквивалентному левой части равенства, все базисные переменные имеют единичные коэффициенты. Поэтому, если прибавить к равенству
, эквивалентному левой части равенства, все базисные переменные имеют единичные коэффициенты. Поэтому, если прибавить к равенству  равенство
равенство  , то в полученном равенстве все базисные переменные будут иметь нулевой коэффициент, так как все свободные переменные вида
, то в полученном равенстве все базисные переменные будут иметь нулевой коэффициент, так как все свободные переменные вида  сократятся, а базисные переменные вида
сократятся, а базисные переменные вида  не войдут в выражение
не войдут в выражение  .
.
Выберем ребро, по которому мы будем перемещаться. Поскольку мы хотим максимизировать  , то необходимо выбрать переменную, которая будет более всех уменьшать выражение
, то необходимо выбрать переменную, которая будет более всех уменьшать выражение
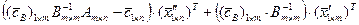 ,
,
(на первом шаге  ).
).
Для этого выберем переменную, которая имеет наибольший по модулю отрицательный коэффициент. Если таких переменных нет и все коэффициенты этого выражения неотрицательны, то мы пришли в искомую вершину и нашли оптимальное решение. В противном случае начнём увеличивать эту свободную переменную, то есть перемещаться по соответствующему ей ребру. Эту переменную назовём входящей.
Третье действие очередного шага.
Теперь необходимо понять, какая базисная переменная первой обратится в ноль по мере увеличения входящей переменной. Для этого достаточно рассмотреть систему:

При фиксированных значениях свободных переменных система однозначно разрешима относительно базисных, поэтому мы можем определить, какая из базисных переменных первой достигнет нуля при увеличении входящей. Эту переменную назовем выходящей. Это будет означать, что мы натолкнулись на новую вершину. Теперь входящую и выходящую переменную поменяем местами — входящая «войдёт» в множество базисных, а выходящая из них «выйдет» в множество свободных. Присвоим всем свободным переменным нулевые значения, вычислим базисные.
Точка  с известными на данный момент значениями является новой вершиной, в которой значение целевой функции больше, чем в предыдущей.
с известными на данный момент значениями является новой вершиной, в которой значение целевой функции больше, чем в предыдущей.
|
из
5.00
|
Обсуждение в статье: Первое действие первого шага |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

