 |
Главная |
Точность и объем имитационных экспериментов
|
из
5.00
|
Нам необходимо провести определенное количество экспериментов с целью получения заданной статистической точности получения результатов.
Например: пусть нам необходимо оценить некоторый параметр α, проведя серию опросов и получая выборку  . Определим
. Определим  . И тогда возникает задача обеспечить оценку параметра α среднего значения
. И тогда возникает задача обеспечить оценку параметра α среднего значения  с точностью
с точностью  :
: 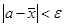 .
.
Вероятность того, что данное условие выполняется будем называть достоверностью, а величину  - достоверным интервалом:
- достоверным интервалом:

Дадим этой функции частотную интерпретацию, то есть если для оценки параметра α систематически использовать величину среднего значения с точностью  и достоверностью
и достоверностью  , то на каждые 100 случаев использования данного интервала 100
, то на каждые 100 случаев использования данного интервала 100  раз условие будет выполняться, и 100
раз условие будет выполняться, и 100  не будет выполняться.
не будет выполняться.
Случай 1.:
Рассматривается вероятность выполнения некоторой задачи. Мы ее отождествляем с вероятностью появления некоторого события А, тогда целью моделирования является оценка вероятности появления этого события. В процессе реализации можно события А поставить в соответствие некоторую величину  , которая принимает значения:
, которая принимает значения:
 с вероятностью P
с вероятностью P
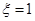 с вероятностью (1-P),
с вероятностью (1-P),
тогда мат. ожидание равняется:

Соответственно дисперсия:

Также мы показали, что для оценки вероятностей может быть использованная частота, которая в нашем случае не что другое как

а если это так, то
 ;
; 
Используя центральную предельную теорему, можно утверждать, что при достаточную большом числе реализаций N частота  направляется к нормальному распределению, и соответствующим условием этой вероятности будет:
направляется к нормальному распределению, и соответствующим условием этой вероятности будет:
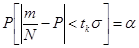
где  - квантиль нормального распределения, где
- квантиль нормального распределения, где  - квантиль
- квантиль  определяется соответствующим значением достоверного интервала, и находится по таблице, так как они связаны между собою функцией Лапласа.
определяется соответствующим значением достоверного интервала, и находится по таблице, так как они связаны между собою функцией Лапласа.
Случай 2.:
Пусть нас интересует проблема оценки некоторой случайной величины (некоторый показатель эффективности системы, связанный функцией с ее параметром), дальше все проходит по предшествующему случаю:
 - оценка среднего по числу реализаций.
- оценка среднего по числу реализаций.
По центральной предельной теореме при достаточно большом среднем арифметическом мы имеем распределение, близкий к нормального с мат. ожиданием и дисперсией соответственно:


и выполняется условие для вероятности, что



Замечание 1:
Как в первому, так и в втором случае число реализаций N зависит от независимой P та  , которые мы бы хотели оценить.
, которые мы бы хотели оценить.
Для определения этого используется метод предварительной пристрелки, то есть используется  опросов. Определяется или оценка частоты, или дисперсии
опросов. Определяется или оценка частоты, или дисперсии  ,
,  . После этого эти величины подставляют в исходные формулы и рассчитывают N.
. После этого эти величины подставляют в исходные формулы и рассчитывают N.
В (2) случае иногда проверяют неравенство  .
.
Замечание 2:
Для того, чтобы объем испытаний N был по возможности меньшим, желательно оценивать параметры тех случайных величин, которые имеют дисперсию и вероятность близкую до 0,5.
|
из
5.00
|
Обсуждение в статье: Точность и объем имитационных экспериментов |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

