Построение математической модели

Аналитическое выражение целевой функции с учетом результатов, полученных выше, запишется в следующем виде:

Таким образом при известных условиях работы системы необходимо определить оптимальную структуру системы. то есть такое количество требований , которые минимизируют величину критерия оптимизации.

Исследование математической модели

Запишем критерий оптимизации в виде (обозначив первое слагаемое через и превратив второе слагаемое):

Как можно видеть, первое слагаемое не зависит от . Для определения минимального значения целевой функции предположим, что оно достигается для - мин. Тогда:

Найдем соответствующие значения для и :

Теперь находим:

Аналогично определяется:

В итоге получаем неравенство, используя которое можно легко определить оптимальную структуру одноканальной замкнутой системы, зная соответствующую входную информацию. Значение , которое удовлетворяет неравенству, обеспечивает минимальное значение критерия оптимизации целевой функции. Чтобы определить оптимальное значение достаточно про табулировать значение следующего неравенства:

где

Задача синтеза(оптимизации) многоканальной замкнутой системы массового обслуживания с ожиданием.

Постановка задачи и выбор критерия оптимизации

Пусть исследуется некоторая многоканальная замкнутая система массового обслуживания. Известные характеристики каналов обслуживания и характеристики требований, которые поступают на обслуживание. необходимо определить такую структуру многоканальной системы. чтобы эффективность системы была максимальной. В качестве критерия оптимизации принимаем целевую функцию , то есть удельные приведенные затраты, то есть затраты, которые приходятся на одно обслуживание. Будем использовать обозначения и допущения те же, что и для одноканальной замкнутой системы. Аналитическое выражение критерия оптимизации для определения оптимальной структуры многоканальной замкнутой системы массового обслуживания будет выглядеть следующим образом:

- число каналов обслуживания в системе.

Используя раньше полученные зависимости представляем исходное аналитическое представление в следующем виде:

1) вероятность того, что в системе на обслуживании находится требований:

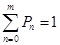
вероятность простоя из-за отсутствия требований в системе: