Результаты решения задачи синтеза робастного управления для стабилизации маятника при неопределенных возмущениях и параметрических изменениях

Как показано в [1], задача синтеза робастного управления в виде обратной связи по состоянию для системы (5.2) с неопределенными возмущениями из (5.3) и параметрическими изменениями, представленными в виде (5.6) с матрицей D, удовлетворяющей ограничению (5.7), сводится к одной из следующих задач оптимизации с ЛМН:

или

при ограничениях

(5.8)

, (5.9)

где минимизация проводится по матричным переменным 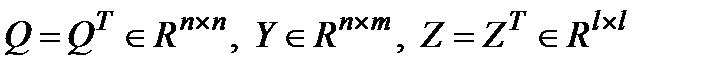, скалярным параметрам q>0, α>0. определяет при фиксированных q и α определяет матрицу предельного инвариантного эллипсоида для вектора состояния x(t), матрицу 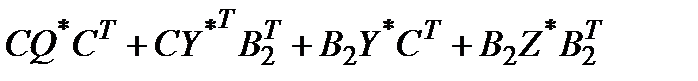предельного ограничивающего эллипсоида для вектора выхода z(t) системы (5.4) и матрицу коэффициентов соответствующего регулятора по состоянию .

Для решении задач при ограничении (5.8) и при ограничениях (5.8),(5.9) была разработана программа, текст которой представлен ниже.

step = 0.25;

begin_val = 2.0;%1.9969;%1.7250;%

end_val = 2.5;%1.9969;%0.2;%-min(eig(A-B*K));

min_tr_Z = 1000000;

%figure (3)

% Синтез робастного регулятора по состоянию при учете неопределенных ограниченных возмущений и параметрических изменений

% Оптимизация по параметрам q и alf путем перебора с уменьшающимся шагом

while step>0.001

for q = begin_val:step:end_val

for alf = 0.11:0.01:0.11

cvx_begin sdp

variable Qs(n1, n1) symmetric;

variable Zs(1,1) symmetric;

variable Ys(1, n1) ;

minimize( trace(C*Qs*C'+C*Ys'*B2'+B2*Ys*C'+B2*Zs*B2'))

%minimize( trace(Qs))

subject to

Qs >= eye(2)*1e-3;

[A*Qs + Qs*A'+B1*Ys+Ys'*B1'+q*Qs+(D*D')/q+alf*gam*(M*M') Qs*N';

N*Qs -alf*eye(2)]< 0; %условие асимптотич устойчивости

[Zs Ys;

Ys' Qs]>=0;

% [Qs eye(2); eye(2) 50*eye(2)]>0;

%norm(Ys, 'fro')<=15;

cvx_end

Qsf = double(Qs)

Y=double(Ys);

K=Y/Qsf;

Z=double(Zs);

%trZ=trace(Qsf);

trZ=trace(C*Qsf*C'+C*Y'*B2'+B2*Y*C'+B2*Z*B2');

if min_tr_Z > trZ

min_tr_Z = trZ

Q_min = Qsf

K_min=K

q_min = q

alf_min=alf

end;

end;

end;

step = step*0.5;

begin_val = q_min-2*step;

end_val = q_min+2*step;

end;

Q1=Q_min

K1=K_min

q1=q_min

alf1=alf_min

A1=A+B1*K1;

С помощью разработанной программы была решена задача минимизации trace (Q) при ограничениях (5.8) и дополнительных ограничениях, обеспечивающих ограниченность коэффициентов усиления регулятора:

[Qs eye(2); eye(2) 50*eye(2)]>0;

norm(Ys, 'fro')<=15;

В результате при q₀₁ =0.1, α₀₁=2 получена матрица минимального инвариантного эллипсоида

,

и коэффициенты K₀₁=[–120.0643 –75.4271] робастного регулятора по состоянию. Матрица замкнутой системы имеет собственные значения [–1.6303, –73.7968]. На рисунке 5.2 показан переходный процесс в исходной нелинейной системе с полученным робастным регулятором при учете внешнего возмущения w=sin(cos(3*t)).

Рисунок 5.2. Переходный процесс в системе с робастным регулятором K₀₁ с 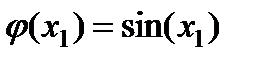при начальных отклонениях x₀=[5 2] и действии возмущения w=sin(cos(3*t))

Для интегрирования исходной системы использовалась функция Mayat_Integr_01.

Для оценивания состояния исходной нелинейной системы с учетом неопределенных возмущений и параметрических изменений было получено на интервале [0,10с] частное решение Q(t) матричной системы сравнения

(5.10)

при q =0.1, α=2, K=K₀₁ и начальной матрице . На рисунке 5.3 показаны сечения эволюционирующего инвариантного эллипса, определяемого матрицей Q(t) в дискретные моменты времени. Начальный эллипс показан пунктирной линией, эллипс, соответствующий матрице показан сплошной линией.

Рисунок 5.3. Сечения эволюционирующего инвариантного эллипса, получаемые в результате численного интегрирования МСС (5.10) при учете регулятора K₀₁

Текст программы для численного интегрирования системы сравнения представлен ниже. Для вычисления правых частей МСС (5.9) используется функция Prav_Lin_Mayat_1rob.

% Оценивание состояния маятника с неопределенными возмущениями с помощью

% матричной системы сравнения

t0=0; tk=10;

Q=Q01+eye(2);

vec_Q = [Q(:,1); Q(:,2)];

[t,H] = ode15s(@(t,vec_Q) Prav_Lin_Mayat_1rob(t,vec_Q,A01,D,q01,alf01,gam,M,N),[t0 tk],vec_Q);

MQ = [];

nh=length(H(:,1));

t(nh)

nn=1;

figure(2)

for i = 1:nn:nh

MQ = [H(i,1) H(i,2); H(i,3) H(i,4)];

MQ=(MQ+MQ')/2;

E = ellipsoid(MQ);

%pEs = projection(E, BB);

plot(E, 'b');grid on;hold on;

end;

plot(E, 'r');grid on;hold on;

 

function dQ=Prav_Lin_Mayat_1rob(t,vec_Q,A,D,q,alf,gam,M,N)

% Вычисление правой части матричной системы сравнения

Q = [ vec_Q(1) vec_Q(2); vec_Q(3) vec_Q(4)];

dQQ= A*Q + Q*A' +q*Q+(D*D')/q+alf*gam*(M*M')+Q*(N'*N)*Q/alf;

dQQ=(dQQ+dQQ')/2;

dQ = reshape(dQQ,4,1);

Также с помощью разработанной программы была решена задача минимизации trace при ограничениях (5.8),(5.9). Получены значения q₁ = 2.5, α₁=0.11, матрица предельного инвариантного эллипса для состояний и коэффициенты K₁=[–11.7002 –6.9773] робастного регулятора по состоянию. Матрица замкнутой системы имеет собственные значения [–3.0192, –3.9581]. На рисунке 5.4 показаны минимальные предельные инвариантные эллипсы для вектора состояний системы с робастными регуляторами K₀₁ (штриховая линия) и K₁ (пунктирная линия). На рисунке 5.5 показан переходный процесс в исходной нелинейной системе с полученным робастным регулятором K₁ по углу (сплошная линия) и по угловой скорости (пунктирная линия) при учете внешнего возмущения w=sin(cos(3*t)).

Рисунок 5.4. Минимальные предельные инвариантные эллипсы для вектора состояний системы с робастными регуляторами K₀₁ (штриховая линия) и K₁ (сплошная линия)

Рисунок 5.5. Переходный процесс в системе с робастным регулятором K₁ с 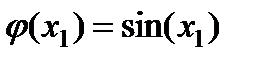при начальных отклонениях x₀=[5 2] и действии возмущения w=sin(cos(3*t))

Для оценивания состояния исходной нелинейной системы с учетом неопределенных возмущений и параметрических изменений было получено на интервале [0,10с] частное решение Q(t) матричной системы сравнения (5.10) при q =0.11, α=2.5, K=K₁ и начальной матрице . На рисунке 5.6 показаны сечения эволюционирующего инвариантного эллипсоида, определяемого матрицей Q(t) в дискретные моменты времени. Начальный эллипсоид показан пунктирной линией, эллипсоид, соответствующий матрице 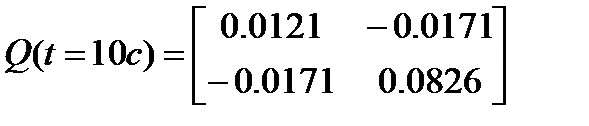показан сплошной линией. Отметим, что эта матрица совпадает с матрицей предельного инвариантного эллипса.

Рисунок 5.3. Сечения эволюционирующего инвариантного эллипса, получаемые в результате численного интегрирования МСС (5.10) при учете регулятора K₁

С помощью программы из п. 2.1 при q₁ =1.8250, q₂=2 произведен синтез наблюдателя состояния с постоянными коэффициентами L₁ =[9.9437 30.4212]. При этом получена следующая матрица предельного инвариантного эллипса, ограничивающего ошибку оценивания

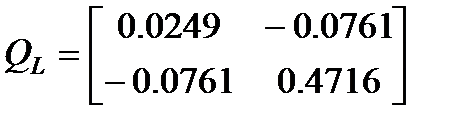, а также матрица 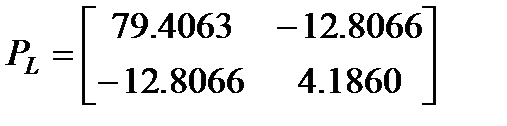. Матрица наблюдателя при этом имеет собственные значения –4.9718±2.4397i.

С помощью вызова функции Observ_Mayat_Integr_01, текст которой представлен в п.2.1, получены переходные процессы в исходной нелинейной системе с робастными регуляторами с коэффициентами K₀₁, K₁ и наблюдателем состояния с постоянными коэффициентами L₁ при действии внешнего возмущения w=-sin(2*cos(3*t)) и погрешности измерений угла, задаваемой датчиком случайных чисел (показаны на рисунках 5.4 и 5.5 соответственно).

Также с помощью вызова функции Prav_CS_Nabl_Mayat_1, текст которой представлен в п.2.2, получены переходные процессы в исходной нелинейной системе с робастными регуляторами с коэффициентами K₀₁, K₁ и наблюдателем состояния с зависимыми от времени и определяемыми по выражению (2.10) коэффициентами при действии внешнего возмущения w=-sin(2*cos(3*t)) и погрешности измерений угла, задаваемой датчиком случайных чисел (показаны на рисунках 5.6 и 5.7 соответственно).

Рисунок 5.4. Переходные процессы в исходной системе (сплошная и штриховая линии) с робастным регулятором K₀₁ по выходу наблюдателя и наблюдателе (пунктирная и штрих-пунктирная линии) с постоянными коэффициентами L₁ при действии возмущений и погрешностей измерений

Рисунок 5.5. Переходные процессы в исходной системе (сплошная и штриховая линии) с робастным регулятором K₁ по выходу наблюдателя и наблюдателе (пунктирная и штрих-пунктирная линии) с постоянными коэффициентами L₁ при действии возмущений и погрешностей измерений

Рисунок 5.6. Переходные процессы в исходной системе (сплошная и штриховая линии) с робастным регулятором K₀₁ по выходу наблюдателя и наблюдателе (пунктирная и штрих-пунктирная линии) с определяемыми по выражению (2.10) коэффициентами при учете возмущений и погрешности измерений угла

Рисунок 5.7. Переходные процессы в исходной системе (сплошная и штриховая линии) с робастным регулятором K₁ по выходу наблюдателя и наблюдателе (пунктирная и штрих-пунктирная линии) с определяемыми по выражению (2.10) коэффициентами при учете возмущений и погрешности измерений угла

Заключение

Разработанные ранее в [1-6] методы и алгоритмы анализа динамики, оценивания состояния и синтеза управления для непрерывных систем при неопределенных внешних возмущениях и параметрических изменениях реализованы в виде комплекса программ для пакета MatLab и апробированы на модели математического мятника. Полученные результаты демонстрирует их высокую эффективность в решении задач анализа, оценивания состояния и управления в условиях информационных неопределенностей и ограничений. Эффективность заключается в наиболее полном учете различных информационных ограничений и информации о неопределенностях при синтезе управления и анализе динамики, в обеспечении гарантированности получаемых оценок, в обеспечении ограничений на управление из условия реализуемости, снижении энергетических затрат на управление.

Литература

1. Маликов А.И. Методические материалы для магистров по дисциплине «Современные проблемы теории управления». Казань: КНИТУ КАИ. 2014. 98 с.

2. Баландин Д.В., Коган М.М. Синтез законов управления на основе линейных матричных неравенств. М.:Физматлит, 2007. 280 с.

3. ElBsat M. N. Finite-Time Control and Estimation of Nonlinear Systems with Disturbance Attenuation/ Dissertations (2009) Milwaukee, Wisconsin: Marquette University, 2012. 206 c.http://epublications.marquette.edu/dissertations_mu/206/

4. Поляк Б.Т., Хлебников М.В., Щербаков П. С. Нелинейные системы с ограниченными или мультипликативными возмущениями //Проблемы устойчивости и управления. Сборник научных статей, посвященный 80-летию академика В.М.Матросова. Москва: Физматлит, 2013. С. 270-299.

5. Маликов А.И. Метод матричных систем сравнения в анализе и синтезе систем управления с неопределенностями // Аналитическая механика, устойчивость и управление: Труды X Международной Четаевской конференции. Т. 2. Секция 2. Устойчивость. Казань, 12 – 16 июня 2012 г. Казань: Изд-во Казан. гос. техн. ун-та, 2012. С.360-370

6 . Guo Y, Yao Y, Wang S., Yang B, Liu K, Zhao X. Finite-time control with H-infinity constraints of linear time-invariant and time-varying systems//J Control Theory Appl. 2013, 11 (2). P. 165–172.