 |
Главная |
Одновременный синтез регулятора с наблюдателем состояния по результатам измерений
|
из
5.00
|
Задачи синтеза регулятора в виде обратной связи по состоянию (теорема 3) и синтеза наблюдателя (теорема 4) могут быть решены одновременно путем решения задачи оптимизации следов матриц предельных инвариантных эллипсоидов, ограничивающих выход для исходной системы с неопределенными возмущениями и ошибки оценивания. Данная задача решается как задача оптимизации с линейными матричными неравенствами. Текст программы для одновременного синтеза регулятора с наблюдателем для исходной автономной системы представлен ниже (Prrim_mayatnik_.m).
% Синтез регулятора по выходу с наблюдателем состояния для линеаризованной % системы на основе решения ЛМН
step1 = 0.05;
step2 = step1;
begin_val1 = 0.15;
end_val1 = 0.25;
begin_val2 = 0.4;%
end_val2 = 0.6;
min_tr_Z = 1000000;
figure (4)
% Оптимизация по параметрам q1 и q2 путем перебора с уменьшающимся шагом
while ((step1+step2)>0.05)
for q1 = begin_val1:step1:end_val1
for q2 = begin_val2:step2:end_val2
cvx_begin sdp
variable Qs1(n1, n1) symmetric;
variable Ys(1, n1) ;
variable Zs(1,1) symmetric;
variable Qs(n1, n1) symmetric;
variable Ps(n1, n1) symmetric;
variable YLs(n1, 1) ;
minimize( trace(C*Qs*C'+C*Qs1*C'+C*Ys'*B2'+B2*Ys*C'+B2*Zs*B2'))
subject to
Qs1>=eye(2)*1e-3;
[A*Qs1 + Qs1*A'+B1*Ys+Ys'*B1'+q0*Qs1 D;
D' -q0*eye(l)]< 0; %условие асимптотич устойчивости
[Zs Ys;
Ys' Qs1]>=0;
[A'*Ps + Ps*A-YLs*Cy-Cy'*YLs'+(q1+q2)*Ps Ps*D YLs;
D'*Ps -q1 0;
YLs' 0 -q2*R2_1]< 0; %условие асимптотич устойчивости
Qs >= eye(2)*1e-8;
[Qs eye(1.2);
eye(1.2) Ps]>=0.0;%eye(1.4)*1e-5;
cvx_end
Qsf = double(Qs)
Qsf1 = double(Qs1)
Psf = double(Ps)
Y=double(Ys);
Z=double(Zs);
YL=double(YLs);
K=Y/Qsf1;
L=Qsf*YL;
trZ=trace(C*(Qsf+Qsf1)*C'+C*Y'*B2'+B2*Y*C'+B2*Z*B2');
if min_tr_Z > trZ
min_tr_Z = trZ
Q_min = Qsf;
Q_min1 = Qsf1;
P_min = Psf;
L_min=L;
K_min=K;
q_min1 = q1
q_min2 = q2
end;
end;
step1= step1*0.5;
begin_val1 = q_min1-2*step;
end_val1 = q_min1+2*step;
end;
step2= step2*0.5;
begin_val2 = q_min2-2*step;
end_val2 = q_min2+2*step;
end;
Qsf2=Q_min1;
QL2=Q_min
PL2=P_min
L2=L_min;
K2=K_min;
q11=q_min1;
q12=q_min2;
AL2=A-L2*Cy;
eig(AL2)
ABK2=A+B1*K2;
eig(ABK2)
figure (8)
E = ellipsoid(QL);
%pEs = projection(E, BB);
plot(E, 'r');grid on;hold on;
При тех же параметрах q0=3.5969, q1 =0.25 q2 =0.6 получены коэффициенты регулятора K2 и наблюдателя L2, которые совпадают соответственно с K1 и L1. На рисунке 2.5 представлены переходные процессы в исходной системе с регулятором по выходу наблюдателя с полученными коэффициентами K2 и L2. На рисунке 2.6 показаны переходные процессы в исходной системе с регулятором по состоянию наблюдателя коэффициенты которого зависят от частного решения матричной системы сравнения (2.5) и определяются по соотношению (2.10).
Рисунок 2.5. Переходные процессы в исходной системе (синий и красный) с регулятором по состоянию наблюдателя и наблюдателе (черный и зеленый) при действии возмущений и погрешностей измерений
Рисунок 2.6. Переходные процессы в исходной системе (синий и красный) с регулятором по состоянию наблюдателя и наблюдателе (черный и зеленый), с зависимыми от частного решения МСС коэффициентами
Как видно из рисунков 2.5,2.6 при использовании для восстановления вектора состояния наблюдателя с зависимыми от частного решения матричной системы сравнения коэффициентами, регулятор по состоянию наблюдателя обеспечивает такую же точность стабилизации при действии возмущений при меньшем перерегулировании и за меньшее время.
Пример решения задач оценивания состояния и синтеза управления в виде обратной связи по состоянию и по выходу (по состоянию наблюдателя) для простейшей системы с неопределенными нелинейностями и возмущениями
Постановка задачи
Рассматривается динамическая система, представленная следующей моделью в пространстве состояний в непрерывном случае
 (3.1)
(3.1)
где  - вектор состояния,
- вектор состояния, 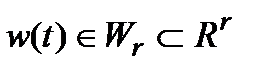 - входное возмущение,
- входное возмущение,  - вектор управляемого выхода,
- вектор управляемого выхода, 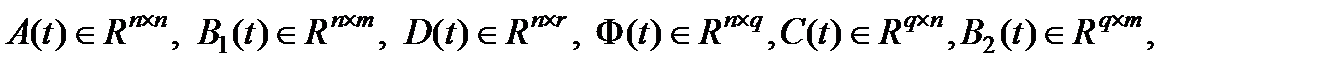 - известные матрицы с непрерывными и ограниченными элементами при всех
- известные матрицы с непрерывными и ограниченными элементами при всех 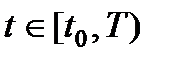 , T>t0 заданная константа (при рассмотрении на конечном интервале) или T=¥ (при рассмотрении на бесконечном интервале).
, T>t0 заданная константа (при рассмотрении на конечном интервале) или T=¥ (при рассмотрении на бесконечном интервале).
Нелинейная векторная функция 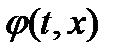 удовлетворяет коническому (обобщенному секторному) условию, заданному в виде:
удовлетворяет коническому (обобщенному секторному) условию, заданному в виде:
 (3.2)
(3.2)
где 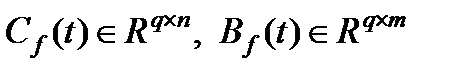 - известные матрица с непрерывными и ограниченными элементами при всех
- известные матрица с непрерывными и ограниченными элементами при всех 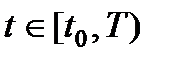 . Здесь как и раньше
. Здесь как и раньше 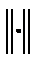 означает евклидову норму вектора,
означает евклидову норму вектора, 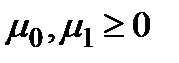 - заданные параметры.
- заданные параметры.
Предположим также, что для внешних возмущений, являющихся непрерывными функциями, выполняется ограничение (1.5).
Предполагается, что пара (A(t),D(t)) –управляема, а матрица C(t) является матрицей полного ранга строк.
Требуется на заданном интервале времени получить эллипсоидальную оценку множества состояний для процессов системы (3.1), начинающихся из заданного эллипсоида 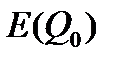 при нелинейностях, удовлетворяющих (3.2) и неопределенных возмущениях из (1.5). Кроме того задача состоит в синтезе закона управления в виде обратной связи по состоянию (1.6) или по выходу ( по состоянию наблюдателя), стабилизирующего замкнутую систему и подавляющего начальные отклонения и воздействие внешних возмущений в смысле минимальности ограничивающего эллипсоида для выхода z при любой нелинейности из (3.2).
при нелинейностях, удовлетворяющих (3.2) и неопределенных возмущениях из (1.5). Кроме того задача состоит в синтезе закона управления в виде обратной связи по состоянию (1.6) или по выходу ( по состоянию наблюдателя), стабилизирующего замкнутую систему и подавляющего начальные отклонения и воздействие внешних возмущений в смысле минимальности ограничивающего эллипсоида для выхода z при любой нелинейности из (3.2).
|
из
5.00
|
Обсуждение в статье: Одновременный синтез регулятора с наблюдателем состояния по результатам измерений |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

