 |
Главная |
Оценивание состояния системы с неопределенными нелинейностями и внешними неопределенными ограниченными возмущениями
|
из
5.00
|
Оценивание состояния системы (3.1) с нелинейностями из (3.2) и неопределенными возмущениями из (1.5) будет осуществляться в виде эволюционирующего инвариантного эллипсоида, матрица которого будет определяться по частному решению матричной системы сравнения или дифференциальных линейных матричных неравенств.
Теорема 3.1. Эллипсоид  , где
, где  есть решение матричной системы дифференциальных уравнений
есть решение матричной системы дифференциальных уравнений
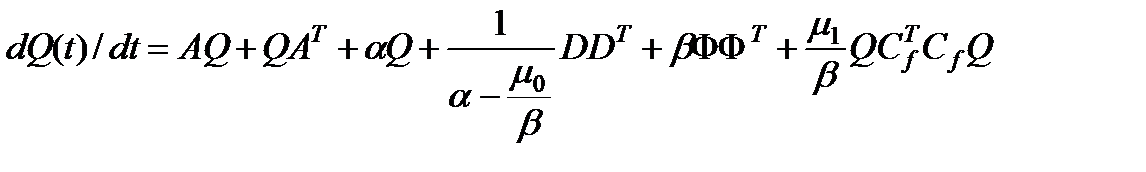 (3.3)
(3.3)
является инвариантным для траекторий системы (3.1), стартующих из начального эллипсоида  .
.
Доказательство теоремы 3.1. Определим функцию  ,
,  . Для любого
. Для любого  имеет место
имеет место  . Для того чтобы траектории x(t)=
. Для того чтобы траектории x(t)=  системы (3.1) не покидали эллипсоид
системы (3.1) не покидали эллипсоид  , достаточно потребовать, чтобы при
, достаточно потребовать, чтобы при  , при всех допустимых внешних возмущениях из (1.5) и при нелинейностях
, при всех допустимых внешних возмущениях из (1.5) и при нелинейностях  из (3.2) выполнялось
из (3.2) выполнялось
 ,
,
где  - производная функции
- производная функции  в силу системы (3.1). Вычислим
в силу системы (3.1). Вычислим
 .
.
Далее, используя очевидное неравенство
 ,
,
справедливое для любых векторов  и любого скаляра или любой непрерывной функции времени
и любого скаляра или любой непрерывной функции времени  , получаем
, получаем
 ,
,
где  - скаляры или непрерывные функции времени. С учетом ограничений на нелинейности (3.2) и внешние возмущения (1.5), а также предположения
- скаляры или непрерывные функции времени. С учетом ограничений на нелинейности (3.2) и внешние возмущения (1.5), а также предположения  отсюда имеем:
отсюда имеем:


при условии 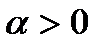 и
и  . Последнее неравенство записывается в виде
. Последнее неравенство записывается в виде  . Тогда можно выбрать
. Тогда можно выбрать  .
.
Будем определять матрицу Q(t) из матричного дифференциального уравнения
 ,
,
где 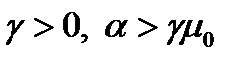 .
.
Умножая это уравнение слева и справа на матрицу Q(t)>0, вводя обозначение  и учитывая, что
и учитывая, что  , приходим к уравнению (3.3). Теорема доказана.
, приходим к уравнению (3.3). Теорема доказана.
Теорема 3.2. Эллипсоид  является инвариантным для решений системы (3.1) , если его матрица
является инвариантным для решений системы (3.1) , если его матрица  удовлетворяет дифференциальным линейным матричным неравенствам (ДЛМН)
удовлетворяет дифференциальным линейным матричным неравенствам (ДЛМН)
 . (3.4)
. (3.4)
при всех 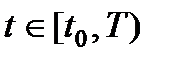 и некоторых
и некоторых  .
.
Доказательство теоремы 3.2 аналогично доказательству теоремы 3.1, только определять матрицу Q(t) будем не из уравнения (3.3) а из дифференциального матричного неравенства
 , (3.5)
, (3.5)
где 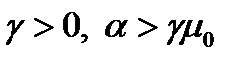 ,
,  . Воспользовавшись леммой дополнения Шура, из (3.5) имеем
. Воспользовавшись леммой дополнения Шура, из (3.5) имеем
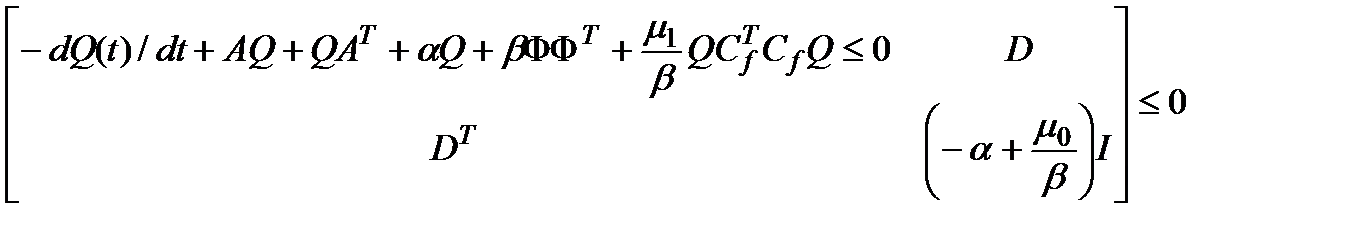
Еще дважды воспользовавшись леммой дополнения Шура, приходим к ДЛМН (3.4).
Следует отметить, что в автономной линейной системе инвариантный эллипсоид с постоянной матрицей Q*, определяемой на основе решения алгебраического уравнения Ляпунова (или разрешимости ЛМН, полученных из (3.4) при dQ/dt=0) будет являться притягивающим, т.е. множеством, к которому будут стремиться все решения с любыми начальными данными и при внешних возмущениях, удовлетворяющих (1.5). В нелинейной автономной системе инвариантный эллипсоид будет притягивающим только для решений, с начальными данными, принадлежащими области притяжения некоторого предельного множества, которое будет принадлежать указанному инвариантному эллипсоиду.
Замечание 3.1. Матричная система дифференциальных уравнений (3.3) является матричной системой сравнения (МСС) для исходной нелинейной системы с неопределенными возмущениями, так как правая часть ее удовлетворяет условию квазимонотонности по Q относительно конуса G+. Поэтому она обладает следующими свойствами:
1). Положительность решений – если  (или
(или 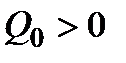 ), то
), то  (соответственно
(соответственно  ) для всех
) для всех  .
.
2) Монотонность решений – для любых  таких, что
таких, что  имеет место
имеет место  для всех
для всех  .
.
В автономном случае – свойствами:
3) Инвариантность множества  , где
, где  : множество
: множество  в пространстве матриц G+ положительно инвариантно для решений
в пространстве матриц G+ положительно инвариантно для решений 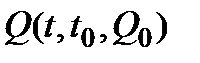 МСС с
МСС с  . Кроме того, найдется
. Кроме того, найдется  такое, что имеет место
такое, что имеет место
 .
.
4) Сходимость решений: если матрица A+BK является гурвицевой, т.е удовлетворяет условию  , где
, где  - собственные значения матрицы замкнутой системы, а параметр q удовлетворяет условию
- собственные значения матрицы замкнутой системы, а параметр q удовлетворяет условию 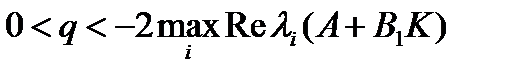 , то существует предел
, то существует предел  , к которому сходятся решения
, к которому сходятся решения  но не для любых
но не для любых  , как было в случае линейных систем, а только для некоторых
, как было в случае линейных систем, а только для некоторых  . В этом случает матрица
. В этом случает матрица  будет определять предельный инвариантный эллипсоид для решений исходной системы (1.4) с неопределенными возмущениями из (1.5).
будет определять предельный инвариантный эллипсоид для решений исходной системы (1.4) с неопределенными возмущениями из (1.5).
Замечание 3.2. Указанные свойства имеют место для любой автономной системы с неопределенными нелинейностями из (3.2) и неопределенными ограниченными возмущениями из (1.5). Так же как в случае линейных систем, они позволяю контролировать процесс получения гарантированных оценок при вычислениях.
|
из
5.00
|
Обсуждение в статье: Оценивание состояния системы с неопределенными нелинейностями и внешними неопределенными ограниченными возмущениями |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

