 |
Главная |
Алгебраическое дополнение и минор элемента матрицы. Разложение определителей по строке и столбцу
|
из
5.00
|
Минором элемента  матрицы А называется определитель матрицы, полученной из А вычеркиванием строки и столбца, содержащих
матрицы А называется определитель матрицы, полученной из А вычеркиванием строки и столбца, содержащих  . Минор элемента
. Минор элемента  обозначается как Mij.
обозначается как Mij.
Рассмотрим выражение (2.1) для определителя матрицы А. Соберем вместе все слагаемые, содержащие элемент 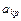 и вынесем
и вынесем 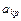 за скобки. Выражение, оставшееся в скобках, называется алгебраическим дополнением элемента
за скобки. Выражение, оставшееся в скобках, называется алгебраическим дополнением элемента 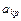 . Обозначается как Akp.
. Обозначается как Akp.
Замечание 2.1. Минор и алгебраическое дополнение элемента матрицы существуют только для квадратных матриц!
Рассмотрим матрицу (Aij), которая отличается от матрицы А только тем, что на месте элементов  в матрице (Aij) стоят их алгебраические дополнения Aij . Транспонируем матрицу (Aij). Полученная таким образом матрица
в матрице (Aij) стоят их алгебраические дополнения Aij . Транспонируем матрицу (Aij). Полученная таким образом матрица  (Aij)T называется союзной матрицей (по отношению к матрице А).
(Aij)T называется союзной матрицей (по отношению к матрице А).
Теорема о связи минора элемента матрицы с его алгебраическим дополнением. Алгебраическое дополнение Aij элемента 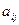 матрицы А и его минор Mij связаны соотношением
матрицы А и его минор Mij связаны соотношением
 . (2.3)
. (2.3)
Пример 2.4. Пусть 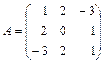 . Тогда M11=1, A11=
. Тогда M11=1, A11= 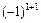 M11 =1; M13=
M11 =1; M13= 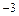 , A13=
, A13= 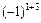 M13 =
M13 = 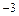 ; M32=2, A32=
; M32=2, A32= 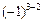 M32 =
M32 = 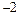 .
.
Теорема о разложении определителя по строке (столбцу).Определитель равен сумме произведений всех элементов любой строки (столбца) матрицы на их алгебраические дополнения:
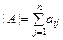 Aij (разложение по i-й строке); (2.4)
Aij (разложение по i-й строке); (2.4)
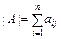 Aij (разложение по j-му столбцу). (2.5)
Aij (разложение по j-му столбцу). (2.5)
Следствие. Из (2.3), (2.4) и (2.5) следует, что
 Mij (разложение по i-й строке); (2.6)
Mij (разложение по i-й строке); (2.6)
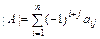 Mij (разложение по j-му столбцу). (2.7)
Mij (разложение по j-му столбцу). (2.7)
Формулы (2.6) и (2.7) служат основой для вычисления определителей методом разложения их по строке (столбцу), который состоит в непосредственном использовании этих формул.
Пример 2.5. 1) пусть 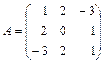 . Вычисление определителя
. Вычисление определителя 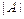 методом разложения его по второму столбцу:
методом разложения его по второму столбцу:
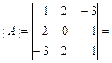 2A12 + 0A22 + 2A32
2A12 + 0A22 + 2A32 
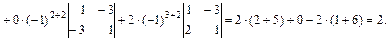
2) вычисление определителя четвертого порядка:
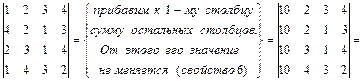
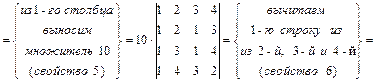
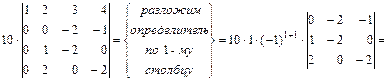
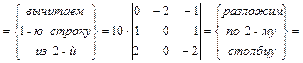

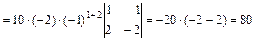 .
.
Теорема об умножении определителей. Пусть A и B – квадратные матрицы размера 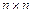 . Тогда определитель произведения матриц равен произведению их определителей:
. Тогда определитель произведения матриц равен произведению их определителей:
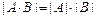 . (2.8)
. (2.8)
Пример 2.6.Пусть 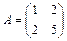 ,
, 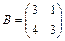 .
.
Тогда  , следовательно,
, следовательно, 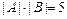 .
.
С другой стороны, 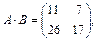 значит
значит 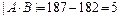 .
.
Таким образом, 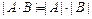 .
.
Задачи
Вычислить определители второго порядка:
2.1. а) 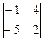 ; б)
; б) 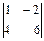 ; в)
; в) 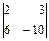 ; г)
; г) 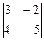 ; д)
; д)  .
.
2.2. а) 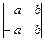 ; б)
; б) 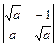 ; в)
; в) 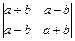 ; г)
; г) 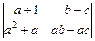 .
.
2.3. а)  ; б)
; б) 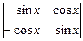 ; с)
; с) 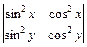 .
.
Решить уравнения относительно 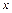 :
:
2.4. 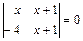 . 2.5.
. 2.5. 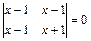 . 2.6.
. 2.6. 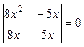 .
.
Вычислить определители третьего порядка:
2.7. а) 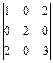 ; б)
; б) 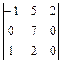 ; в)
; в) 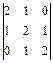 ; г)
; г) 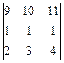 .
.
2.8. а) 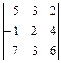 ; б)
; б) 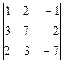 ; в)
; в) 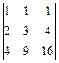 ; г)
; г) 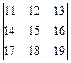 .
.
2.9. а) 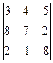 ; б)
; б) 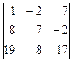 ; в)
; в) 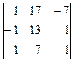 ; г)
; г) 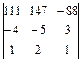 .
.
2.10. а) 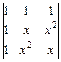 ; б)
; б)  ; в)
; в) 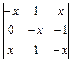 ; г)
; г) 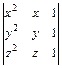 .
.
2.11. а) 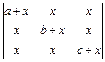 ; б)
; б) 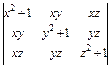 ; в)
; в) 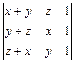 .
.
2.12. а) 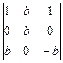 ; б)
; б) 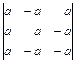 ; в)
; в) 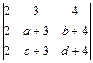 .
.
2.13. а) 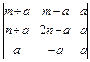 ; б)
; б) 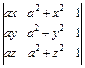 ; в)
; в) 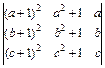 .
.
2.14. а) 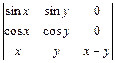 ; б)
; б) 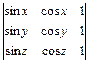 .
.
2.15. Показать, что  делится на
делится на  и
и 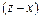 .
.
2.16. Показать, что 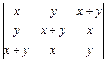 делится на
делится на 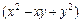 и
и 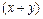 .
.
Доказать следующие тождества:
2.17. 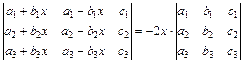 .
.
2.18.  .
.
2.19.  .
.
2.20. 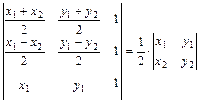 .
.
Решить относительно 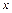 уравнения:
уравнения:
2.21. а) 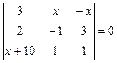 ; б)
; б) 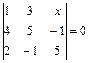 ; в)
; в) 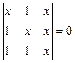 .
.
2.22. 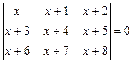 . 2.23.
. 2.23.  .
.
Решить относительно 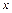 неравенства:
неравенства:
2.24.  . 2.25.
. 2.25. 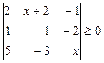 .
.
2.26. 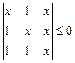 . 2.27.
. 2.27. 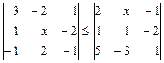 .
.
2.28. 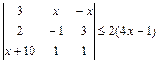 .
.
2.29. Построить графики функций:
а) 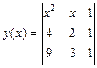 ; б)
; б) 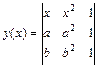 ,
, 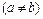 .
.
Вычислить определители четвертого порядка:
2.30. а) 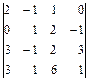 ; б)
; б) 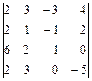 ; в)
; в) 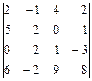 .
.
2.31. а) 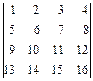 ; б)
; б) 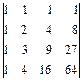 ; в)
; в) 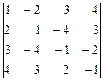 .
.
2.32. а) 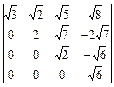 ; б)
; б) 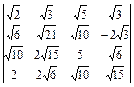 .
.
2.33. а) 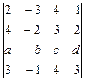 ; б)
; б)  ; в)
; в) 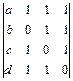 .
.
2.34. а) 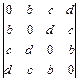 ; б)
; б) 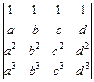 ; в)
; в) 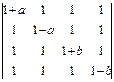 .
.
Вычислить определители пятого порядка:
2.35. а) 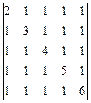 ; б)
; б) 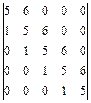 ; в)
; в) 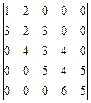 .
.
2.36. а) 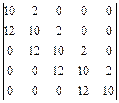 ; б)
; б)  .
.
Вычислить определители n-го порядка:
2.37. 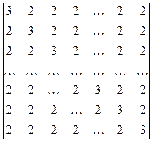 ; 2.38.
; 2.38. 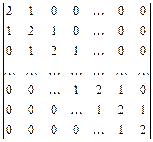 .
.
2.39. 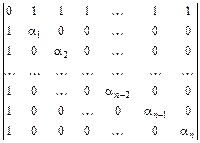 .
.
2.40. 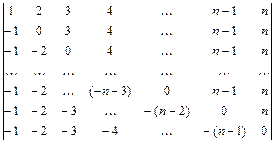 .
.
2.41. 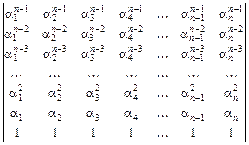 .
.
2.42. Вычислить определитель 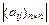 , где
, где 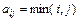 .
.
2.43. Вычислить определитель 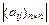 , где
, где 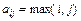 .
.
РАНГ МАТРИЦЫ
Основные понятия и примеры
Ранг матрицы – это особая числовая функция, заданная на множестве матриц. В отличие от определителя, ранг матрицы существует для матрицы любого порядка.
Прежде чем дать определение ранга матрицы, рассмотрим понятие минора матрицы.
Минором k-го порядка матрицы А называется определитель матрицы, составленной из элементов каких-либо k выделенных строк и каких-либо k выделенных столбцов исходной матрицы А.
Понятие минора k-го порядка широко используется в линейной алгебре. В отличие от минора элемента матрицы, минор k-го порядка не связан с конкретным элементом матрицы и существует для любых, а не только для квадратных матриц. Миноров k-го порядка для любой матрицы может быть много. Например, для матрицы порядка 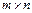 количество миноров k-го порядка определяется числом
количество миноров k-го порядка определяется числом
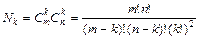 .
.
Главным, или угловым минором k-го порядка матрицы называется минор, составленный из первых k строк и первых k столбцов этой матрицы.
Рангом матрицы А называется наивысший порядок отличных от нуля миноров этой матрицы. Обозначается как 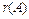 .
.
Пример 3.1. Пусть 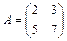 ,
, 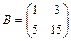 ,
, 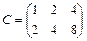 . Тогда
. Тогда 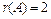 ,
, 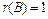 ,
, 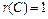 .
.
Любой отличный от нуля минор матрицы, порядок которого равен рангу этой матрицы, называется ее базисным минором.
|
из
5.00
|
Обсуждение в статье: Алгебраическое дополнение и минор элемента матрицы. Разложение определителей по строке и столбцу |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

