 |
Главная |
Метод окаймляющих миноров
|
из
5.00
|
Пусть некоторый минор  k-го порядка не равен нулю, т.е.,
k-го порядка не равен нулю, т.е., 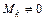 . Тогда ранг
. Тогда ранг 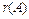 матрицы А по крайней мере равен k, т.е.,
матрицы А по крайней мере равен k, т.е.,  . Рассмотрим все окаймляющие, т.е. содержащие в себе минор
. Рассмотрим все окаймляющие, т.е. содержащие в себе минор  миноры (k+1)-го порядка
миноры (k+1)-го порядка  . Если все они равны нулю, то ранг матрицы А равен k:
. Если все они равны нулю, то ранг матрицы А равен k:  . В противном случае найдется
. В противном случае найдется  , и вся процедура повторяется.
, и вся процедура повторяется.
Пример 3.3. Пусть 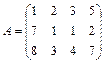 . Так как среди элементов матрицы есть ненулевые, то
. Так как среди элементов матрицы есть ненулевые, то  .
.
Находим любой минор второго порядка, не равный нулю, например, такой:  . Это означает, что
. Это означает, что  . Рассматриваем все окаймляющие
. Рассматриваем все окаймляющие 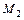 миноры третьего порядка. Их всего два, и оба равны нулю:
миноры третьего порядка. Их всего два, и оба равны нулю:  ;
; 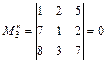 . Таким образом, ранг матрицы равен двум:
. Таким образом, ранг матрицы равен двум: 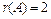 .
.
Метод элементарных преобразований
Метод основан на том факте, что элементарные преобразования не меняют ранга матрицы. Проделывая элементарные преобразования исходной матрицы, ее приводят к виду, когда все элементы вне главной диагонали равны нулю, а среди элементов главной диагонали только первые s отличны от нуля:
 ,
,  ,
, 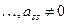 . Тогда
. Тогда 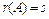 .
.
Пример 3.4. Пусть 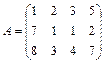 . Рассмотрим следующую цепочку элементарных преобразований матрицы А:
. Рассмотрим следующую цепочку элементарных преобразований матрицы А:


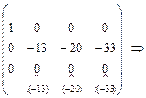
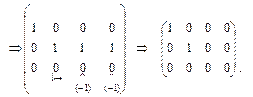
Таким образом, 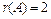 .
.
Задачи
Найти ранг матрицы методом окаймляющих миноров:
3.1.  . 3.2.
. 3.2. 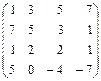 . 3.3.
. 3.3.  .
.
3.4.  . 3.5.
. 3.5. 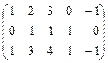 .
.
3.6.  . 3.7.
. 3.7.  . 3.8.
. 3.8. 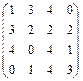 .
.
3.9. 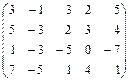 .
.
Вычислить ранг матрицы методом элементарных преобразований:
3.10.  . 3.11.
. 3.11. 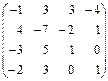 .
.
3.12. 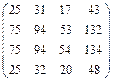 . 3.13.
. 3.13. 
3.14.  .
.
3.15.  .
.
3.16.  .
.
Вычислить ранг матрицы:
3.17. 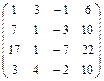 . 3.18
. 3.18  .
.
3.19.  .
.
3.20  . 3.21
. 3.21 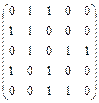 .
.
3.22. 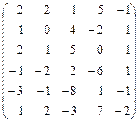 . 3.23
. 3.23  .
.
Чему равен ранг матрицы A при различных значениях  ?
?
3.24.  . 3.25.
. 3.25.  . 3.26.
. 3.26.  .
.
3.27. Доказать, что если произведение матриц AB определено, то
 .
.
3.28. Пусть A – невырожденная матрица, а матрицы B и C таковы, что 
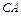 определены. Доказать, что
определены. Доказать, что 
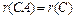 .
.
3.29. Доказать, что 
3.30. Найти базисные миноры для матриц 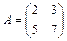 ,
, 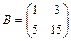 ,
, 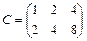 ,
,  .
.
ОБРАТНАЯ МАТРИЦА
Основные сведения
Пусть задана квадратная матрица А. Матрица B, обладающая свойством  , называется обратной матрицей к А. Обозначается как
, называется обратной матрицей к А. Обозначается как  .
.
Матрица А называется ортогональной, если 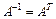 .
.
Теорема об обратной матрице. Справедливы утверждения:
1) Матрица А обладает обратной матрицей  тогда и только тогда, когда
тогда и только тогда, когда  .
.
2) Обратная матрица  единственна и может быть найдена по формуле
единственна и может быть найдена по формуле
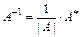 , (4.1)
, (4.1)
где  – союзная матрица.
– союзная матрица.
Следствие. Из теоремы о связи минора элемента матрицы с его алгебраическим дополнением и теоремы об обратной матрице следует, что
 . (4.2)
. (4.2)
Формула (4.2) лежит в основе метода поиска обратной матрицы, называемого методом союзной матрицы и изложенного ниже.
Методы поиска обратной матрицы
Метод союзной матрицы
В основе данного метода лежит теорема об обратной матрице. Метод состоит в выполнении следующих шагов:
Шаг 1. Вычисляется определитель матрицы, по отношению к которой ищется обратная матрица. Если данный определитель равен нулю, то делается заключение об отсутствии обратной матрицы.
Шаг 2. Вычисляются алгебраические дополнения элементов исходной матрицы и по формуле (4.2) находится искомая обратная матрица.
Пример 4.1. Пусть 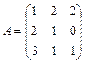 .
.
Шаг 1:  , следовательно,
, следовательно,  существует.
существует.
Шаг 2: A11  M11
M11  ; A12
; A12  M12
M12  ;
;
A13  M13
M13  ; A21
; A21 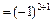 M21
M21  ;
;
A22 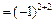 M22
M22  ; A23
; A23 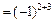 M23
M23  ;
;
A31  M31
M31  ; A32
; A32 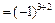 M32
M32  ;
;
A33 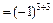 M33
M33  .
.
Таким образом,
 .
.
Метод союзной матрицы имеет существенный недостаток: он требует слишком много вычислений. При поиске обратной матрицы размера  необходимо вычислить
необходимо вычислить  миноров порядка
миноров порядка 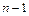 . Например, при поиске обратной матрицы размера
. Например, при поиске обратной матрицы размера  необходимо вычислить 25 определителей 4-го порядка. С вычислительной точки зрения более целесообразным является метод элементарных преобразований.
необходимо вычислить 25 определителей 4-го порядка. С вычислительной точки зрения более целесообразным является метод элементарных преобразований.
|
из
5.00
|
Обсуждение в статье: Метод окаймляющих миноров |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

