 |
Главная |
Характеристические числа и векторы
|
из
5.00
|
Любое линейное преобразование  однозначно определяет матрицу А оператора
однозначно определяет матрицу А оператора  в заданном базисе пространства
в заданном базисе пространства  .
.
Ненулевой вектор 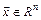 называется характеристическим (собственным) вектором квадратной матрицы
называется характеристическим (собственным) вектором квадратной матрицы  , принадлежащим ее собственному значению
, принадлежащим ее собственному значению  , если после преобразования
, если после преобразования  он переходит в вектор, отличающийся от
он переходит в вектор, отличающийся от  лишь на постоянный множитель
лишь на постоянный множитель  , то есть, если
, то есть, если
 . (6.7)
. (6.7)
Числовой множитель  называется характеристическим корнем (собственным значением) матрицы А оператора
называется характеристическим корнем (собственным значением) матрицы А оператора  .
.
Для любого собственного вектора  матрицы А, принадлежащего собственному значению
матрицы А, принадлежащего собственному значению  и любого числа
и любого числа  вектор
вектор  также является собственным вектором матрицы А, принадлежащим собственному значению
также является собственным вектором матрицы А, принадлежащим собственному значению  .
.
Многие прикладные задачи экономики сводятся к проблеме отыскания собственных значений и собственных векторов матриц.
Уравнение (6.7) может быть представлено в виде
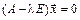 . (6.8)
. (6.8)
Матрица  называется характеристической матрицей.
называется характеристической матрицей.
Нетривиальное (ненулевое) решение уравнения (6.8) существует лишь в том случае, если определитель характеристической матрицы равен нулю:
 . (6.9)
. (6.9)
Уравнение (6.9) называется характеристическим уравнением. Если А – матрица порядка 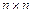 , то характеристическое уравнение является алгебраическим уравнением степени n относительно
, то характеристическое уравнение является алгебраическим уравнением степени n относительно  :
:

 .
.
Это уравнение имеет n не обязательно различных корней  причем некоторые из них могут быть комплексными числами. Каждому из этих характеристических корней соответствует характеристический вектор, определенный с точностью до постоянного множителя.
причем некоторые из них могут быть комплексными числами. Каждому из этих характеристических корней соответствует характеристический вектор, определенный с точностью до постоянного множителя.
Пример 6.2. Характеристическое уравнение для матрицы  имеет вид
имеет вид  . Уравнение имеет два корня:
. Уравнение имеет два корня:  ,
,  . Характеристическими векторами, соответствующими
. Характеристическими векторами, соответствующими  и
и  , являются вектора
, являются вектора  и
и  , где с – произвольная константа. Произвольные константы часто исключают из рассмотрения, вводя нормализованные векторы. В данном примере нормализованными векторами являются
, где с – произвольная константа. Произвольные константы часто исключают из рассмотрения, вводя нормализованные векторы. В данном примере нормализованными векторами являются  и
и  .
.
Свойства характеристических корней
1. Сумма характеристических корней равна следу матрицы:
2.  .
.
3. Произведение характеристических корней равно определителю матрицы:  .
.
4. Число ненулевых характеристических корней матрицы совпадает с рангом этой матрицы.
5. Характеристическими корнями диагональной матрицы являются элементы ее главной диагонали.
6. Для симметрических матриц все n собственных значений являются вещественными числами.
Согласно теореме Гамильтона-Кэли, матрица А является корнем своего характеристического уравнения:
Теорема Гамильтона-Кэли. Пусть характеристическим уравнением матрицы А является уравнение
 .
.
Тогда справедливо матричное уравнение
 .
.
В некоторых случаях интерес представляет задача отыскания собственных векторов, принадлежащих собственному значению  . Достаточные условия существования такого собственного вектора вытекает из следующей теоремы.
. Достаточные условия существования такого собственного вектора вытекает из следующей теоремы.
Теорема о единичном собственном значении. Если в матрице А сумма элементов каждого столбца равна 1, то имеется собственный вектор, принадлежащий собственному числу 1.
Во многих связанных с отысканием собственных векторов прикладных задачах экономики содержательный смысл имеют только собственные вектора с положительными компонентами. Условия существования таких векторов даются теоремой Фробениуса-Перрона.
Теорема Фробениуса-Перрона. Пусть А – неотрицательная квадратная матрица. Тогда:
1. Максимальное по модулю собственное значение 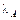 матрицы А неотрицательно. Среди собственных векторов, принадлежащих
матрицы А неотрицательно. Среди собственных векторов, принадлежащих 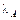 имеется неотрицательный вектор.
имеется неотрицательный вектор.
2. В случае  все неотрицательные собственные векторы матрицы А положительны и принадлежат только ее максимальному по модулю собственному значению
все неотрицательные собственные векторы матрицы А положительны и принадлежат только ее максимальному по модулю собственному значению 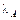 . Кроме того, в этом случае любые два положительных собственных вектора
. Кроме того, в этом случае любые два положительных собственных вектора  и
и  отличаются лишь числовым множителем, то есть,
отличаются лишь числовым множителем, то есть,  .
.
Задачи
В задачах (6.1-6.3) векторы  и
и  заданы своими координатами в некотором базисе G. Доказать, что система
заданы своими координатами в некотором базисе G. Доказать, что система  также является базисом и найти координаты вектора
также является базисом и найти координаты вектора  в этом базисе.
в этом базисе.
6.1.  ,
,  ,
,  ,
,  .
.
6.2.  ,
,  ,
,  ,
,  .
.
6.3.  ,
, 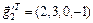 ,
,  ,
,  ,
, 
В задачах (6.4) и (6.5) векторы  и
и  заданы своими координатами в некотором базисе. Требуется доказать, что системы векторов
заданы своими координатами в некотором базисе. Требуется доказать, что системы векторов  и
и  также являются базисами. Найти матрицу перехода
также являются базисами. Найти матрицу перехода  от базиса G к базису
от базиса G к базису  .
.
6.4.  ,
,  ,
,  ;
;  ,
,  ,
,  .
.
6.5.  ,
,  ,
,  ,
,  ;
;



 .
.
Найти ортонормированный базис из собственных векторов и матрицу в этом базисе для линейного оператора, заданного в некотором ортонормированном базисе матрицей А (искомый базис определен неоднозначно):
6.6.  . 6.7.
. 6.7.  . 6.8.
. 6.8.  .
.
|
из
5.00
|
Обсуждение в статье: Характеристические числа и векторы |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

