 |
Главная |
Собственные числа и собственные векторы матрицы
|
из
5.00
|
Число  называется собственным числом матрицы
называется собственным числом матрицы  ,
,
если существует ненулевой вектор  такой, что
такой, что
 .
.
При этом вектор  называется собственным вектором матрицы
называется собственным вектором матрицы  , соответствующим собственному числу
, соответствующим собственному числу  .
.
Характеристическим уравнением матрицы  называется уравнение
называется уравнение
 . (10)
. (10)
Корни  этого уравнения являются собственными числами матрицы А.
этого уравнения являются собственными числами матрицы А.
Рассмотрим систему уравнений
 ,
,
в которой  принимает одно из значений
принимает одно из значений  . Определитель этой системы в силу (10) равен нулю. Следовательно, система определяет с точностью до постоянного множителя собственный вектор
. Определитель этой системы в силу (10) равен нулю. Следовательно, система определяет с точностью до постоянного множителя собственный вектор  , соответствующий данному собственному числу.
, соответствующий данному собственному числу.
Задание 5. Найти собственные числа и собственные векторы матрицы
 .
.
Решение. Составим характеристическое уравнение матрицы А.
 ,
,
или  . Корни этого уравнения
. Корни этого уравнения  являются собственными числами матрицы А.
являются собственными числами матрицы А.
Для отыскания собственных векторов матрицы А используем систему уравнений
 (11)
(11)
полагая в ней поочередно  .
.
1. Пусть  . Тогда система (11) примет вид:
. Тогда система (11) примет вид:

или
 . (12)
. (12)
Полученную систему решим методом Гаусса. Расширенная матрица  системы (12) имеет вид:
системы (12) имеет вид:
 .
.
Приведем матрицу  к трапециевидному виду с помощью элементарных преобразований. Для этого умножим элементы первой строки матрицы
к трапециевидному виду с помощью элементарных преобразований. Для этого умножим элементы первой строки матрицы  на (-3) и сложим с соответствующими элементами второй строки. Получим матрицу
на (-3) и сложим с соответствующими элементами второй строки. Получим матрицу
 ,
,
которая является расширенной матрицей системы
 .
.
Следовательно,  , то есть система имеет бесчисленное множество решений, определяемых равенством
, то есть система имеет бесчисленное множество решений, определяемых равенством  .
.
Таким образом, собственным вектором матрицы А, соответствующим собственному числу  , является ненулевой вектор, определяемый совокупностью чисел
, является ненулевой вектор, определяемый совокупностью чисел  , где t - любое число, отличное от нуля.
, где t - любое число, отличное от нуля.
2. Пусть  . Тогда система (11) примет вид:
. Тогда система (11) примет вид:
 . (13)
. (13)
Решим систему (13) методом Гаусса.
Расширенная матрица системы (13) имеет вид:
 .
.
Приведем матрицу  к трапециевидному виду с помощью элементарных преобразований. Для этого, сначала переставим первую строку матрицы
к трапециевидному виду с помощью элементарных преобразований. Для этого, сначала переставим первую строку матрицы  со второй строкой. Получим:
со второй строкой. Получим:
 .
.
Теперь умножим элементы первой строки матрицы  на 2 и сложим с соответствующими элементами второй строки. Затем умножим элементы первой строки матрицы
на 2 и сложим с соответствующими элементами второй строки. Затем умножим элементы первой строки матрицы  на (-3) и сложим с соответствующими элементами третьей строки. В результате получим:
на (-3) и сложим с соответствующими элементами третьей строки. В результате получим:
 .
.
Далее, сложим элементы второй строки матрицы  с соответствующими элементами третьей строки. Получим матрицу:
с соответствующими элементами третьей строки. Получим матрицу:
 ,
,
которая является расширенной матрицей системы
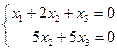 .
.
Следовательно,  , то есть система имеет бесконечное множество решений, определяемых равенством
, то есть система имеет бесконечное множество решений, определяемых равенством  .
.
Таким образом, собственным вектором матрицы А, соответствующим собственному числу  , является ненулевой вектор, определяемый совокупностью чисел
, является ненулевой вектор, определяемый совокупностью чисел  , где t - любое число, отличное от нуля.
, где t - любое число, отличное от нуля.
3) Пусть 
 . Тогда система (11) примет вид:
. Тогда система (11) примет вид:
 (14)
(14)
Решим систему (14) методом Гаусса. Расширенная матрица системы (14) имеет вид:
 .
.
Приведем матрицу  к трапециевидному виду с помощью элементарных преобразований. Сначала поменяем первую строку матрицы
к трапециевидному виду с помощью элементарных преобразований. Сначала поменяем первую строку матрицы  со второй строкой. Получим:
со второй строкой. Получим:
 .
.
Умножим теперь элементы первой строки матрицы  на 5 и сложим с соответствующими элементами второй строки. Затем умножим элементы первой строки матрицы
на 5 и сложим с соответствующими элементами второй строки. Затем умножим элементы первой строки матрицы  на (-3) и сложим с соответствующими элементами третьей строки. В результате получим:
на (-3) и сложим с соответствующими элементами третьей строки. В результате получим:
 .
.
Далее, сложим элементы второй строки матрицы  соответственно с элементами третьей строки. Тогда получим матрицу:
соответственно с элементами третьей строки. Тогда получим матрицу:
 ,
,
которая является расширенной матрицей системы
 .
.
Следовательно,  , то есть система имеет бесчисленное множество решений, определяемых равенством
, то есть система имеет бесчисленное множество решений, определяемых равенством  .
.
Таким образом, собственным вектором матрицы А, соответствующим собственному числу 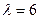 , является ненулевой вектор, определяемый совокупностью чисел
, является ненулевой вектор, определяемый совокупностью чисел  , где t - любое число, отличное от нуля.
, где t - любое число, отличное от нуля.
|
из
5.00
|
Обсуждение в статье: Собственные числа и собственные векторы матрицы |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

