|
Главная |
Метод последовательного исключения неизвестных
|
из
5.00
|
Методом Гаусса решить систему уравнений:
1. 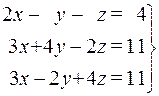 . 2.
. 2. 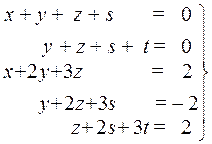 .
.
3. 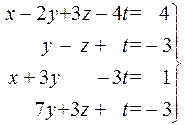 . 4.
. 4. 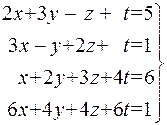 .
.
5. 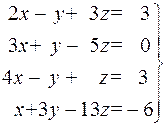 . 6.
. 6.  .
.
7. 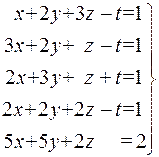 . 8.
. 8. 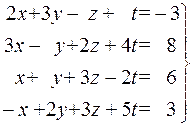 .
.
Вычисление определителей
9.  . 10.
. 10.  . 11.
. 11. 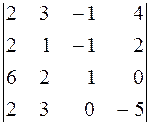 .
.
12.  . 13.
. 13. 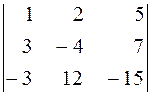 . 14.
. 14.  .
.
15.  . 16.
. 16. 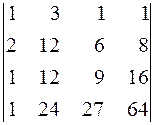 . 17.
. 17.  .
.
18.  . 19.
. 19. 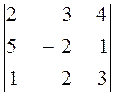 . 20.
. 20. 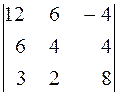 .
.
Правило Крамера
Решить системы уравнений методом определителей:
21. 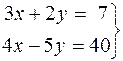 . 22.
. 22. 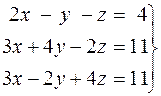 . 23.
. 23.  .
.
24. 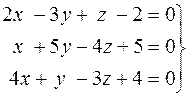 . 25.
. 25.  . 26.
. 26.  .
.
27.  . 28.
. 28.  . 29.
. 29.  .
.
30. 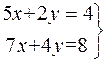 . 31.
. 31.  . 32.
. 32. 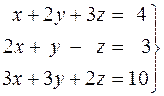 .
.
33. 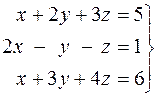 . 34.
. 34.  . 35.
. 35.  .
.
36. 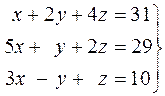 . 37.
. 37.  .
.
38.  . 39.
. 39. 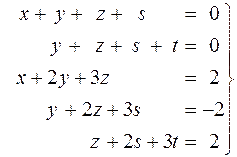 .
.
|
Действия с векторами
40. По сторонам ОА и ОВ прямоугольника ОАСВ отложены единичные векторы 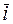 и
и 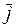 . Выразить через
. Выразить через 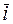 и
и 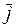 векторы:
векторы: 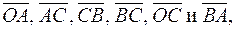 если ОА = 3 и ОВ = 4 (рис. 1).
если ОА = 3 и ОВ = 4 (рис. 1).
41. Пусть на рис.1 М – середина ВС и N – середина АС. Определить векторы 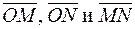
 при ОА = 3 и ОВ = 4.
при ОА = 3 и ОВ = 4.
42. На плоскости даны точки А(0; –2), В(4; 2) и С(4; –2). В начале координат приложены силы  . Построить их равнодействующую
. Построить их равнодействующую 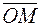 , найти ее проекции на оси координат и величину. Выразить силы
, найти ее проекции на оси координат и величину. Выразить силы 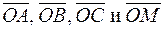 через единичные векторы
через единичные векторы 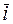 и
и 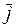 координатных осей.
координатных осей.
43. В прямоугольнике ОАСВ (рис. 1) М и N — середины сторон ВС = 3 и АС = 4. Разложить геометрически и аналитически вектор 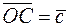 по векторам
по векторам  и
и  .
.
Указание. В условие 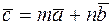 подставить выражения
подставить выражения 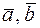 и
и 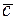 через
через 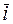 и
и 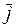 и сравнить коэффициенты слева и справа при
и сравнить коэффициенты слева и справа при 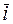 и
и 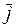 .
.
44. Вектор составляет с осями Ох и Oz углы 40° и 80°. Найти его угол с осью Оу.
45. Радиус-вектор точки М составляет с осью Ох угол 45° и с осью Оу угол 60°. Длина его r = 6. Определить координаты точки М, если ее координата z отрицательна, и выразить вектор  через орты
через орты 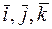 .
.
46. Даны точки А(1; 2; 3) и В(3; –4; 6). Построить вектор 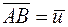 , его проекции на оси координат и определить длину и направление вектора. Построить углы вектора
, его проекции на оси координат и определить длину и направление вектора. Построить углы вектора  с осями координат.
с осями координат.
47. В точке А(2; 1; –1) приложена сила R = 7. Зная две координаты этой силы Х = 2 и Y = –3, определить направление и конец вектора, изображающего силу.
48. На плоскости Оxу даны точки А(4; 2), В(2; 3) и С(0; 5) и построены векторы 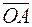 =
= 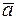 и
и 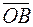 =
= 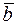 и
и  =
= 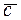 .Разложить геометрически и аналитически вектор
.Разложить геометрически и аналитически вектор 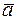 по векторам
по векторам 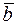 и
и 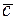 .
.
|
49. В равнобедренной трапеции ОАСВ (рис. 2) угол ВОА = 60°, ОВ = ВС = СА = 2, М и N — середины сторон ВС и АС. Выразить векторы  и
и 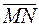 через
через 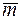 и
и 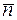 – единичные векторы направлений
– единичные векторы направлений 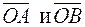 .
.
50. На плоскости даны точки А(3; 3), В(–3; 3) и С(–3; 0). В начале координат приложены силы  . построить равнодействующую
. построить равнодействующую 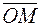 , найти ее проекции на оси координат и величину. Выразить силы
, найти ее проекции на оси координат и величину. Выразить силы 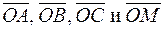 через единичные векторы
через единичные векторы 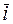 и
и 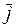 координатных осей.
координатных осей.
51. В трапеции ОАСВ имеем ВС = ОА/3 и ВС||ОА. Разложить геометрически и аналитически вектор 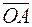 =
= 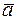 по векторам
по векторам  =
= 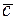 и
и 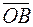 =
= 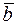 .
.
Указание. Из треугольника ОВС можно 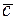 выразить через
выразить через 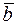 и
и 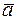 и затем решить полученное уравнение относительно
и затем решить полученное уравнение относительно 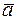 .
.
52.Даны точки А(2; 2; 0) и В(0; –2; 5). Построить вектор 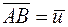 и определить его длину и направление.
и определить его длину и направление.
53. Вектор 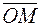 =
= 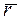 составляет с осями координат равные острые углы. Определить эти углы и построить вектор
составляет с осями координат равные острые углы. Определить эти углы и построить вектор 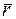 , если его длина равна
, если его длина равна 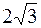 .
.
54. Вектор составляет с осями Оу и Оz углы 60° и 120°. Какой угол он составляет с осью Ох?
55. Даны три последовательные вершины параллелограмма А(1; –2; 3), В(3; 2; 1) и С(6; 4; 4). Найти его четвертую вершину D.
Указание. Из равенства  следует, что равны и их координаты: х – 1 = 6 – 3 и т.д.
следует, что равны и их координаты: х – 1 = 6 – 3 и т.д.
56. На плоскости Оxу построить векторы  и
и 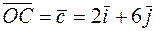 .Разложить геометрически и аналитически вектор
.Разложить геометрически и аналитически вектор 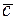 по векторам
по векторам 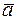 и
и 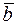 .
.
|
из
5.00
|
Обсуждение в статье: Метод последовательного исключения неизвестных |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы