 |
Главная |
Глава 2. Дифференцирование функций
|
из
5.00
|
Понятие функции
224. Дано: y = sinx; v = lgy; u =  . Выразить u как функцию х.
. Выразить u как функцию х.
225.Следующие сложные функции представить с помощью цепочек, составленных из основных элементарных функций:
1) y = sin3(2x + 1); 2) y =  ; 3) y = sin ln arcctg 2x.
; 3) y = sin ln arcctg 2x.
226. Построить области изменения переменной х, удовлетворяющей неравенствам: 1)  ; 2)
; 2)  ; 3)
; 3)  .
.
227. Найти корни х1 и х2 функции у = 4х - х2 и построить ее график на отрезке [x1 -1; x2 +1].
228. Дано: f (x) = 2x3 -5x2 -23x. Найти все корни уравнения f (x) = f (-2).
229. Найти области определения данных функций:
1)  ; 2)
; 2)  ; 3)
; 3)  ;
;
4)  ; 5)
; 5)  .
.
230. Тождественны ли функции:
1)  и
и 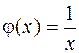 ; 2)
; 2)  и
и 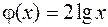 ?
?
231. Какие из указанных ниже функций четны, какие нечетны, какие не являются ни четными, ни нечетными?
1) у = х4 -2х2; 2) y = cos x; 3)  ; 4) y = sin x - cos x;
; 4) y = sin x - cos x;
5) y = tg x; 6)  ; 7)
; 7)  ; 8)
; 8)  ; 9)
; 9)  .
.
232. Найти функцию, обратную данной:
1) y =x2 -2x; 2)  ; 3)
; 3)  .
.
233. Дано: y = 1 + x; z = cos y;  . Выразить v как функцию х.
. Выразить v как функцию х.
234. Следующие сложные функции представить с помощью цепочек, составленных из основных элементарных функций:
1)  ; 2)
; 2)  ; 3) y = arcos ln tg 4x.
; 3) y = arcos ln tg 4x.
235. Построить области изменения переменной х, удовлетворяющей неравенствам: 1)  ; 2)
; 2)  ; 3)
; 3)  .
.
236. Построить графики функций:
1)  ; 2)
; 2) 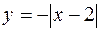 ; 3)
; 3)  .
.
237. Указать два корня уравнения  , если известно, что функция f (x) определена в интервале (-5; 5). Найти все корни данного уравнения для случая, когда f (x) = x2 – 12x + 3.
, если известно, что функция f (x) определена в интервале (-5; 5). Найти все корни данного уравнения для случая, когда f (x) = x2 – 12x + 3.
238. Найти области определения данных функций:
1) 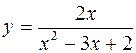 ; 2)
; 2)  ;
;
3)  ; 4)
; 4)  .
.
239. Тождественны ли функции:
1)  и
и  ; 2) f (x) = x и
; 2) f (x) = x и  ?
?
240. Какие из указанных ниже функций четны, какие нечетны, какие не являются ни четными, ни нечетными?
1) у = х - х2; 2) y = 2x; 3) y = sin x; 4) y = 1 - x2; 5) 
6)  ; 7)
; 7)  ; 8)
; 8)  ;
;
241. Найти функцию, обратную данной:
1)  ; 2)
; 2) 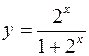 ; 3)
; 3)  .
.
Понятие предела
242. Полагая n = 0, 1, 2, 3, ..., написать последовательность значений переменных:  ,
,  ,
,  .
.
Начиная с какого n модуль каждой из переменной сделается и будет оставаться меньше 0,001, меньше данного  ?
?
243. Доказать, что последовательность  при неограниченном возрастании n стремится к пределу, равному
при неограниченном возрастании n стремится к пределу, равному  , монотонно возрастая. Начиная с какого n, величина
, монотонно возрастая. Начиная с какого n, величина 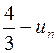 не превосходит данного положительного числа e ?
не превосходит данного положительного числа e ?
244. При неограниченном возрастании х функция  стремится к нулю:
стремится к нулю:  . Каково должно быть N, чтобы из
. Каково должно быть N, чтобы из 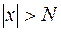 следовало у < e ?
следовало у < e ?
245. Доказать, что  . При каких х значения функции будут отличаться от своего предела меньше чем на 0,01?
. При каких х значения функции будут отличаться от своего предела меньше чем на 0,01?
246. Написать последовательность значений переменной  . Начиная с какого n, модуль разности х - 1 сделается и будет оставаться меньше 0,01, меньше данного положительного e ?
. Начиная с какого n, модуль разности х - 1 сделается и будет оставаться меньше 0,01, меньше данного положительного e ?
247. Доказать, что  стремится к 1 при неограниченном возрастании n. Начиная с какого n абсолютная величина разности между un и 1 не превосходит 10-4 ?
стремится к 1 при неограниченном возрастании n. Начиная с какого n абсолютная величина разности между un и 1 не превосходит 10-4 ?
248. Дано у = х2. Когда x → 2, то y → 4. Каково должно быть d, чтобы из  , следовало
, следовало 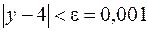 ?
?
249. Доказать, что  . При каких х значения функции будут отличаться от своего предела меньше чем на 0,001 ?
. При каких х значения функции будут отличаться от своего предела меньше чем на 0,001 ?
Нахождение пределов
Найти пределы:
250.  . 251.
. 251.  . 252.
. 252. 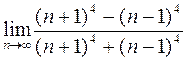 .
.
253.  . 254.
. 254.  . 255.
. 255.  .
.
256.  . 257.
. 257.  . 258.
. 258. 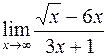 . 259..
. 259.. 
260.  . 261.
. 261.  .
.
262.  . 263.
. 263.  . 264.
. 264.  .
.
265.  . 266.
. 266.  .
.
267.  . 268.
. 268. 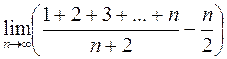 .
.
269. 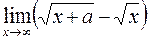 . 270.
. 270.  .
.
271.  . 272.
. 272.  . 273.
. 273.  .
.
274.  . 275.
. 275.  . 276.
. 276.  .
.
277.  . 278.
. 278.  .
.
279.  . 280.
. 280. 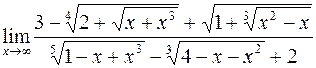 .
.
281.  . 282.
. 282.  . 283.
. 283.  . 284.
. 284.  .
.
285.  . 286.
. 286. 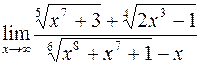 .
.
287.  . 288.
. 288.  .
.
289.  . 290.
. 290.  .
.
–––––––––––––––––––––––––––––
Найти пределы:
291.  . 292.
. 292.  . 293.
. 293.  .
.
294.  . 295.
. 295.  . 296.
. 296.  .
.
297.  . 298.
. 298.  . 299.
. 299.  .
.
300.  . 301.
. 301.  . 302.
. 302.  . 303.
. 303.  .
.
304.  . 305.
. 305.  . 306.
. 306.  .
.
307.  . 308.
. 308.  .
.
309.  . 310.
. 310.  . 311.
. 311.  .
.
312.  . 313.
. 313. 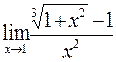 . 314.
. 314.  .
.
315.  . 316.
. 316.  . 317.
. 317.  .
.
318.  . 319.
. 319.  .
.
320.  . 321.
. 321.  . 322.
. 322.  .
.
323.  .
.
§20. Число е. Исследование функции на непрерывность
Найти пределы:
324. 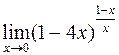 . 325.
. 325. 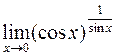 . 326.
. 326.  .
.
Исследовать на непрерывность функции:
327.  . 328.
. 328.  .
.
Найти пределы:
329.  . 330.
. 330.  . 331.
. 331. 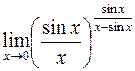 .
.
Исследовать на непрерывность функции:
332.  . 333.
. 333.  .
.
Производная функции
Продифференцировать указанные функции:
334.  . Найти:
. Найти:  .
.
335.  . 336.
. 336.  . 337.
. 337.  .
.
338.  . 339.
. 339.  . 340.
. 340.  .
.
341.  . 242.
. 242.  . 343.
. 343.  .
.
344. 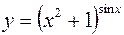 . 345.
. 345. 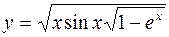 . 347.
. 347.  .
.
346.  . 348.
. 348.  .
.
349.  . Найти:
. Найти:  .
.
350.  . 351.
. 351.  . 352.
. 352.  .
.
353.  . 354.
. 354.  . 355.
. 355. 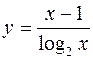 .
.
356.  . 357.
. 357.  . 358.
. 358.  . 359.
. 359.  .
.
360.  . 361.
. 361.  .
.
362.  . 363.
. 363.  .
.
|
из
5.00
|
Обсуждение в статье: Глава 2. Дифференцирование функций |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

