 |
Главная |
Касательная, нормаль, плоскости
|
из
5.00
|
Составить уравнения касательной прямой и нормальной плоскости для данных линий в указанных точках:
555.  в данной точке
в данной точке  .
.
556. y2 + z2 = 25, x2 + y2 = 10 в точке (1; 3; 4).
557. Написать уравнения касательной плоскости к поверхности: z = x2 + 2y2 в точке (1; 1; 3).
558. Написать уравнения нормали к поверхности x2z + y2z = 4 в точке (-2; 0; 1).
Для данных поверхностей найти уравнения касательных плоскостей и нормалей в указанных точках:
559. z = 2x2 – 4y2 в точке (2; 1; 4).
560.  в точке (3; 4; –7).
в точке (3; 4; –7).
Составить уравнения касательной прямой и нормальной плоскости для данных линий в указанных точках:
561.  .
.
562. 2x2 + 3y2 + z2 = 47, x2 + 2y2 = z в точке (–2; 1; 6).
563. Написать уравнение касательной плоскости к поверхности az = x2 + y2 в точках пересечения ее с прямой x = y = z.
564. Написать уравнения нормали к поверхности x2 + y2 - (z - 5)2 = 0 в точке (4; 3; 0).
Для данных поверхностей найти уравнения касательных плоскостей и нормалей в указанных точках:
565. 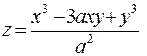 в точке (a; a; –a). 566.
в точке (a; a; –a). 566.  в точке (1; 1;
в точке (1; 1;  ).
).
567. К поверхности x2 + 2y2 + 3z2 = 21 провести касательные плоскости, параллельные плоскости x + 4y + 6z = 0.
Производная по направлению и градиент скалярного поля
Найти градиенты функций в точке A(1; 2):
568. z = 4 – x2 – y2. 569. z = x2 – 2xy + 3y – 1.
570. Найти градиент функции u = ln(x2 + y2 + z2) в точке М0(1; 1; -1).
571. Найти наибольшую крутизну поверхности z2 = xy в точке (4; 2).
572. найти направление и величину наибольшего изменения скалярного поля u(M) = x2y + y2z + z2x в точке M0(1; 0; 0).
573. Найти угол j между градиентами функции 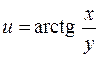 в точках М1(1; 1) и М2(-1; -1).
в точках М1(1; 1) и М2(-1; -1).
574. Найти угол между градиентами функций  и
и  в точке (3; 4).
в точке (3; 4).
575. Найти производную функции z = x2 – 3x2y + 3xy2 + 1 в точке M(3; 1) в направлении, идущем от этой точки к точке (6; 5).
576. Для функции u = x2y + xz2 - 2 найти производную в точке М0(1; 1; -1) по направлению к точке М1(1; -1; 3).
577. Найти производную скалярного поля u = ln(x2 + y2) в точке М0(1; 2) параболы y2 = 4x по направлению этой кривой.
578. Найти производную скалярного поля u = ln (xy + yz + xz) в точке М0(0; 1; 1) по направлению окружности x = cos t, y = sin t, z = 1.
579. Найти градиент функции  в точке (2; 1)
в точке (2; 1)
580. Найти градиент скалярного поля  в точке O(0; 0; 0).
в точке O(0; 0; 0).
581. найти направление и величину наибольшего изменения скалярного поля u(M) = xyz в точке M0(2; 1; –1).
582. Найти угол j между градиентами функции u = (x + y)ex+y в точках М1(0; 0) и М2(1; 1).
583. Найти угол j между градиентами функций  и
и 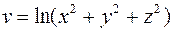 в точке М0(0; 0; 1).
в точке М0(0; 0; 1).
584. Найти производную функции z = arctg xy в точке (1; 1) в направлении биссектрисы первого координатного угла.
585. Для функции u =  найти производную в точке М0(1; 1) по направлению к точке М1(4; 5).
найти производную в точке М0(1; 1) по направлению к точке М1(4; 5).
586. Найти производную функции z = ln (x + y) в точке (1; 2), принадлежащей параболе y2 = 4x, по направлению этой параболы.
587. Найти производную скалярного поля u = arctg  в точке М0(2; -2) окружности x2 + y2 - 4x = 0 вдоль дуги этой окружности.
в точке М0(2; -2) окружности x2 + y2 - 4x = 0 вдоль дуги этой окружности.
588. Найти производную скалярного поля u = x2 + y2 + z2 в точке М0, соответствующей значению параметра t =  по направлению винтовой линии x = Rcos t, y = Rsin t, z = at.
по направлению винтовой линии x = Rcos t, y = Rsin t, z = at.
Глава 4. интегрирование функций
Табличное интегрирование
Найти интегралы:
589.  . 590.
. 590.  . 591.
. 591. 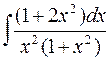 .
.
592.  . 593.
. 593.  . 594.
. 594.  .
.
595. 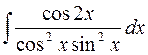 . 596.
. 596.  . 597.
. 597.  .
.
598.  . 599.
. 599.  . 600.
. 600.  . 601.
. 601.  .
.
602.  . 603.
. 603.  . 604.
. 604. 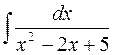 .
.
605.  . 606.
. 606.  . 607.
. 607. 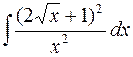 .
.
608.  . 609.
. 609.  . 610.
. 610.  .
.
611.  . 612.
. 612.  . 613.
. 613.  . 614.
. 614.  .
.
615.  . 616.
. 616.  . 617.
. 617.  . 618.
. 618.  .
.
619.  . 620.
. 620.  . 621.
. 621.  . 622.
. 622. 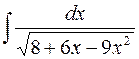 .
.
623. 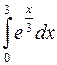 . 624.
. 624.  .
.
|
из
5.00
|
Обсуждение в статье: Касательная, нормаль, плоскости |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

