Функции и их классификацию

Пример 1.Изобразить схематично график функции

y = f(x), удовлетворяющей условиям:

f(0)=0.

График функции изображен на рис. 5.8.

x = –1 – точка разрыва 1-го рода.

Так как то функция непрерывна в точке x = –1 справа.

В точке x = 2 разрыв 2-го рода.

В примерах 2–8 требуется найти точки разрыва функции, установить их характер и изобразить схематично график

функции в окрестности точек разрыва (а если удастся, и во всей области определения).

Пример 2. .

Решение.Функция определена и, следовательно, непрерывна на всей числовой оси за исключением точек x₁ = –3 и x₂ = 3. В этих точках функция терпит разрыв. Найдем односторонние пределы функции в этих точках.

.

Поясним полученный результат. Знаменатель функции при x → –3–0 будет стремиться к нулю, но так как при этом левее точки x = –3 величина x² будет все время оставаться больше числа 9, то разность (x²– 9) будет стремиться к нулю, оставаясь все время положительной. Здесь и далее +0 обозначение бесконечно малой величины, которая стремится к нулю, оставаясь положительной; –0 – обозначение бесконечно малой величины, которая стремится к нулю, оставаясь отрицательной.

Закончим нахождение односторонних пределов:

Все односторонние пределы оказались равны ∞ => x₁= – 3, x₂=3 – точки разрыва второго рода. Изобразим поведение функции в окрестности точек разрыва на основании проведенного исследования (рис. 5.9).

В данном случае легко построить график функции полностью, если найти

Полученный результат означает, что при x → ± ∞ график функции будет прижиматься к оси Ox.

Кроме этого, используя то, что данная функция нечетная и при этом f(0) = 0, можно построить график функции на всей области определения (рис.5.10).

Пример 3. .

Решение.Функция не определена только в точке x =1=> эта точка является точкой разрыва функции. Выясним характер разрыва:

Один из пределов оказался равен ∞ => x=1 – точка разрыва 2-го рода.

Изобразим поведение функции в окрестности точки x=1, при этом учтем, что показательная функция принимает только положительные значения (рис. 5.11).

Чтобы достроить график функции, найдем

график функции при x→± ∞ прижимается к прямой y=1. При построении графика учтем, что (рис. 5.12).

Пример 4.

Решение.Функция f(x) определена на всей числовой оси. Каждая из функций , и 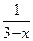в своей области определения непрерывны, следовательно, функция f(x) может иметь разрыв только в точках x₁=0 и x₂=3. Найдем односторонние пределы функции f(x) в этих точках:

.

Пределы конечны и различны => в точке x₁= 0 разрыв 1-го рода. Так как 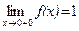и по условию , делаем заключение, что функция y=f(x) непрерывна в точке x=0 справа.

.

Один из пределов оказался равен –∞ => функция f(x) имеет в точке x₂ = 3 разрыв 2-го рода.

График функции f(x) получим, если для 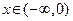построим график функции , на промежутке [0,3] это будет соответствующая часть параболы , для – соответствующая ветвь гиперболы (рис. 5.13).

Пример 5. При каком значении a функция

будет непрерывной в точке x = 3?

Решение.Функция y = f(x) будет непрерывной в точке

x = 3, если в этой точке будет выполнено условие непрерывности, то есть если

.

По условию f(3) = 2³= 8.

Найдем односторонние пределы:

.

Таким образом, функция f(x) будет непрерывной, если 7a – 6 = 8 => a = 2. Геометрически это означает, что в точке x = 3 произойдет «стыковка» графика показательной функции y = 2 ^x и прямой y = 14 – 2x (рис. 5.14).