Тема: Парная линейная регрессия

 

Вопрос: Парная регрессия

А) это модель сезонности

*Б) это модель, где значения зависимой переменной Y рассматривается, как функция одной независимой переменной X

В) моделью тренда и сезонности

 

Вопрос: Выбрать правильный ответ.

Уравнение линейной парной регрессии между зависимой переменной Y и независимой переменной X, где a, b – параметры модели, может иметь вид:

*А) Y=a+bX

Б) Y=aX+bX

В)Y=a-bX

 

Вопрос: Случайная величина

А) некоторое значение из неопределенного набора данных

Б) случайно найденный параметр

*В) это влияние неучтенных факторов, случайных ошибок и особенностей измерения.

 

Вопрос: Метод наименьших квадратов

А) метод поиска минимума функции

*Б) метод оценивания параметров линейной регрессии, минимизирующий сумму квадратов отклонений наблюдений зависимой переменной от искомой линейной функции.

В) метод определения коэффициента роста функции

 

Вопрос: С помощью какого метода можно найти оценки параметра уравнения линейной регрессии:

*А) методом наименьшего квадрата;

Б) корреляционно-регрессионного анализа;

В) дисперсионного анализа.

 

Вопрос: В соотношении МНК сумма квадратов отклонений фактических значений результативного признака от его теоретических значений

А) увеличивается;

*Б) минимизируется;

 

Вопрос: Перечислите методы выбора математической функции

А) аналитический;

*Б) графический;

*В) экспериментальный (табличный).

 

Вопрос: Наиболее наглядным видом выбора уравнения парной регрессии является:

А) аналитический;

*Б) графический;

В) экспериментальный (табличный).

 

Вопрос: Рассчитывать параметры парной линейной регрессии можно, если у нас есть:

А) не менее 5 наблюдений;

*Б) не менее 7 наблюдений;

В) не менее 10 наблюдений.

 

Вопрос: Суть метода наименьших квадратов состоит в:

А) минимизации суммы остаточных величин;

Б) минимизации дисперсии результативного признака;

*В) минимизации суммы квадратов отклонений.

 

Вопрос: Коэффициент b линейного парного уравнения регрессии:

*А) показывает среднее изменение результата с изменением фактора на одну единицу;

Б) оценивает статистическую значимость уравнения регрессии;

В) показывает, на сколько процентов изменится в среднем результат, если фактор изменится на 1%.

 

Вопрос: Метод наименьших квадратов для оценки параметров уравнений регрессии дает хорошие результаты

А) Всегда

*Б) При выполнении определенных предпосылок

В) При большом количестве наблюдений

Г) При небольшом количестве наблюдений

 

Вопрос: На основании наблюдений за 50 семьями построено уравнение регрессии , где – потребление, – доход. Соответствуют ли знаки и значения коэффициентов регрессии теоретическим представлениям?

*А) да;

Б) нет;

В) ничего определенного сказать нельзя.

 

Вопрос: На основании наблюдений за 50 семьями построено уравнение регрессии , где – потребление, – доход? Чему равен параметры парной регрессии b?

А) 284,56;

Б) 0;

*В) 0,672.

 

Вопрос: На основании наблюдений за 50 семьями построено уравнение регрессии , где – потребление, – доход? Чему равен параметры парной регрессии a?

*А) 284,56;

Б) 0;

В) 0,672.

 

Вопрос: Уравнение линейной парной регрессии между зависимой переменной Y и независимой переменной X, где a, b – параметры модели, не может иметь вид:

*А) Y=a+bX²

Б) Y=а+bX

В) Y=a+b₁X₁+b₂X₂

 

Вопрос: Система нормальных уравнений для оценки параметров a и b, имеет вид:

*А)

Б)

В)

 

Вопрос: Параметр a можно найти по формуле

А)

Б)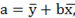

*В)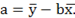

 

Вопрос: Параметр b можно найти по формуле

А) ,

*Б)

В) .

 

Вопрос: Ковариация признаков -

А)

*Б) ,

В)

 

Вопрос: Дисперсия признака x

*А)

Б)

В)

 

Вопрос: Ковариация –

А) числовая характеристика случайных величин

*Б) числовая характеристика совместного распределения двух случайных величин, равная математическому ожиданию произведения отклонений этих случайных величин от их математических ожиданий.

В) характеристика случайной величины, определяемая как математическое ожидание квадрата отклонения случайной величины от ее математического ожидания

 

Вопрос: Дисперсия –

А) числовая характеристика совместного распределения двух случайных величин, равная математическому ожиданию произведения отклонений этих случайных величин от их математических ожиданий.

Б) сумма произведений значений случайной величины на соответствующие вероятности

*В) характеристика случайной величины, определяемая как математическое ожидание квадрата отклонения случайной величины от ее математического ожидания.

 

Вопрос: Математическое ожидание

*А) – сумма произведений значений случайной величины на соответствующие вероятности

Б) числовая характеристика совместного распределения двух случайных величин, равная математическому ожиданию произведения отклонений этих случайных величин от их математических ожиданий.

В) характеризует наличие или отсутствие линейной связи между переменными

 

Вопрос: Суть коэффициента корреляции состоит в следующем:

А) характеризует совместное распределение двух случайных величин

*Б) характеризует наличие или отсутствие линейной связи между переменными

В) сумма произведений значений случайной величины на соответствующие вероятности

 

Вопрос: Коэффициент корреляции находится по формуле

А)

*Б)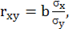

В)

 

Вопрос: Линейный коэффициент корреляции находится в пределах

А) от 0 до 1;

Б) любой.

*В)

 

Вопрос: Если линейный коэффициент корреляции близко к единице, тем

*А) сильнее линейная связь между факторами,

Б) слабее линейная связь между факторами,

В) связь единичная.

 

Вопрос: Суть коэффициента детерминации состоит в следующем:

*А) оценивает качество модели из относительных отклонений по каждому наблюдению;

Б) характеризует долю дисперсии результативного признака , объясняемую регрессией, в общей дисперсии результативного признака;

В) характеризует долю дисперсии , вызванную влиянием не учтенных в модели факторов.

 

Вопрос: коэффициент детерминации находится в пределах

*А) [0,1],

Б) [0,1),

В) [-1,1].

 

Вопрос: Величина -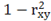

А) оценивает качество модели из относительных отклонений по каждому наблюдению;

Б) характеризует долю дисперсии результативного признака , объясняемую регрессией, в общей дисперсии результативного признака;

*В) характеризует долю дисперсии , вызванную влиянием не учтенных в модели факторов.

 

Вопрос: Качество модели из относительных отклонений по каждому наблюдению оценивает:

А) коэффициент детерминации ;

Б) -критерий Фишера;

*В) средняя ошибка аппроксимации .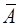

 

Вопрос: Средняя ошибка аппроксимации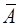

*А) ,

Б)

В)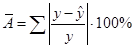

 

Вопрос: Качество построенной модели оценивается как хорошее, если средняя ошибка аппроксимации 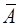не превышает

А) 2-3%,

*Б) 8-10%,

В) 20-25%.

 

Вопрос: Значимость уравнения регрессии в целом оценивает:

*А) -критерий Фишера;

Б) -критерий Стьюдента;

В) коэффициент детерминации .

 

Вопрос: -критерий Фишера

А)

Б)

*В)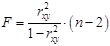

 

Вопрос: Остаточная сумма квадратов равна нулю:

*А) когда правильно подобрана регрессионная модель;

Б) когда между признаками существует точная функциональная связь;

В) никогда.

 

Вопрос: Объясненная (факторная) сумма квадратов отклонений в линейной парной модели имеет число степеней свободы, равное:

А) ;

*Б) ;

В) .

 

Вопрос: Остаточная сумма квадратов отклонений в линейной парной модели имеет число степеней свободы, равное:

А) ;

Б) ;

*В) .

 

Вопрос: Общая сумма квадратов отклонений в линейной парной модели имеет число степеней свободы, равное:

*А) ;

Б) ;

В) .

 

Вопрос: Какое уравнение регрессии нельзя свести к линейному виду:

А) ;

Б) :

*В) .

 

Вопрос: Коэффициент регрессии в уравнении 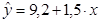, характеризующем связь между объемом реализованной продукции (млн. руб.) и прибылью предприятий автомобильной промышленности за год (млн. руб.) означает, что при увеличении объема реализованной продукции на 1 млн. руб. прибыль увеличивается на:

А) 0,5 %;

Б) 0,5 млн. руб.;

В) 500 тыс. руб.;

*Г) 1,5 млн. руб.

 

Вопрос: Дано уравнение регрессии 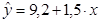, характеризующее связь между объемом реализованной продукции (млн. руб.) и прибылью предприятий автомобильной промышленности за год (млн. руб). : Чему равен коэффициент b

А) 9.2

Б) -1.5

*В) 1.5

 

Вопрос: Дано уравнение регрессии 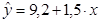, характеризующее связь между объемом реализованной продукции (млн. руб.) и прибылью предприятий автомобильной промышленности за год (млн. руб). : Чему равен коэффициент a

*А) 9.2

Б) -1.5

В) 1.5

 

Вопрос: Известно, что между величинами X и Y существует отрицательная связь. В каких пределах находится парный коэффициент корреляции?

*А) от -1 до 0;

Б) от 0 до 1;

В) от –1 до 1.

 

Вопрос: По 16 наблюдениям построено парное линейное уравнение регрессии. Для проверки значимости коэффициента регрессии вычислено t_на6л=2.5.

*А) Коэффициент незначим при a=0.01;

Б) Коэффициент значим при a=0.05;

В) Коэффициент значим при a=0.1.

 

Вопрос: Известно, что между величинами X и Y существует положительная связь. В каких пределах находится парный коэффициент корреляции?

А) от -1 до 0;

*Б) от 0 до 1;

В) от –1 до 1.

 

Вопрос: Величина парного коэффициента корреляции, равная 2, свидетельствует:

А) о слабой их зависимости;

Б) о сильной взаимосвязи;

*В) об ошибках в вычислениях.

 

Вопрос: Величина индекса корреляции, равная -2,5, свидетельствует:

А) о слабой их зависимости;

Б) о сильной взаимосвязи;

*В) об ошибках в вычислениях.

 

Вопрос: Какие из приведенных чисел могут быть значениями парного коэффициента корреляции:

*А) 1;

Б) 2;

В) -2,7;

*Г) -0,7.

 

Вопрос: Какие из приведенных чисел могут быть значениями парного коэффициента корреляции:

А) 1,4;

*Б) -1;

В) -2,7;

 

Вопрос: Какие из приведенных чисел могут быть значениями коэффициента детерминации:

*А) 0,4;

Б) 1,1;

В) -0,9.

 

Вопрос: Какие из приведенных чисел могут быть значениями коэффициента детерминации:

*А) 0,56;

Б) -1;

В) -0,97;

 

Вопрос: Отметьте правильную форму линейного уравнения регрессии:

А) ŷ ;

Б) ŷ ;

*В) ŷ .

 

Вопрос: Оценка статистической значимости парного коэффициента корреляции основывается:

*А) На использовании t – статистики;

Б) На использовании F – статистики;

В) На использовании ;

 

Вопрос: При каком значении средней относительной ошибки по модулю модель имеет высокую точность:

*А) менее 10%;

Б) выше 10%;

В) от 10% до 20%.

 

Вопрос: Стандартное отклонение случайной величины x ( σ_x)

А) числовая характеристика совместного распределения двух случайных величин, равная математическому ожиданию произведения отклонений этих случайных величин от их математических ожиданий

*Б) мера разброса случайной величины вокруг среднего значения.

В) сумма произведений значений случайной величины на соответствующие вероятности

 

Вопрос: это -

А) числовая характеристика совместного распределения двух случайных величин

Б) мера разброса случайной величины вокруг среднего значения.

*В) Стандартная ошибка коэффициента регрессии

 

Вопрос: По 15 наблюдениям построено уравнение регрессии: . Для проверки значимости уравнения вычислено наблюдаемое значение t - статистики: 2.1 Вывод:

А) Уравнение незначимо при a= 0,01;

*Б) Уравнение незначимо при a = 0,1;

*В) Уравнение незначимо при a = 0,05.

 

Вопрос: По 17 наблюдениям построено уравнение регрессии: . Для проверки значимости уравнения вычислено наблюдаемое значение t - статистики: 2,5. Вывод:

А) Уравнение незначимо при a= 0,05;

*Б) Уравнение незначимо при a = 0,01;

В) Уравнение незначимо при a = 0,1.

 

Вопрос: По 20 наблюдениям построено уравнение регрессии: . Для проверки значимости уравнения вычислено наблюдаемое значение t - статистики: 1.9. Вывод:

*А) Уравнение значимо при a= 0,10;

Б) Уравнение значимо при a = 0,01;

В) Уравнение значимо при a = 0,05.

 

Вопрос: уровень значимости a

А) числовая характеристика совместного распределения двух случайных величин

*Б) вероятность отторгнуть правильную гипотезу, при условии что она верна

В) Стандартная ошибка коэффициента регрессии

 

Вопрос: Получено уравнение данные связи расходов населения на продукты питания с уровнем доходов семьи.

А) Т.е. с увеличением дохода семьи на 1000 руб. расходы на питание увеличиваются на 168% .

Б) Т.е. с увеличением дохода семьи на 1000 руб. расходы на питание уменьшаются на 168 руб.

*В) Т.е. с увеличением дохода семьи на 1000 руб. расходы на питание увеличиваются на 168 руб.

 

Вопрос: Коэффициент детерминации

А) показывает, что уравнением регрессии объясняется 9,87% дисперсии результативного признака, а на долю прочих факторов приходится остальное.

Б) показывает, что уравнением регрессии объясняется 0,987% дисперсии результативного признака, а на долю прочих факторов приходится лишь 99%.

*В) показывает, что уравнением регрессии объясняется 98,7% дисперсии результативного признака, а на долю прочих факторов приходится лишь 1,3%.

 

Вопрос: Если , то это означает

*А) Уравнение статистически значимое и надежное,

Б) уравнение статистически незначимое и ненадежное,

В) уравнение неправильно построено.

 

Вопрос: Если , то это означает

А) Уравнение статистически значимое и надежное,

*Б) уравнение статистически незначимое и ненадежное,

В) уравнение неправильно построено.

 

Вопрос: Критерий Стьюдента предназначен

А) для определения значимости параметра а,

*Б) для определения значимости каждого коэффициента регрессии

В) для определения значимости уравнения.

 

Вопрос: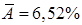

А) говорит о плохом качестве уравнения регрессии.

*Б) говорит о хорошем качестве уравнения регрессии, т.е. свидетельствует о хорошем подборе модели к исходным данным.

В) свидетельствует о не правильном подборе модели к исходным данным.

 

Вопрос: Критические значения критерия Фишера определяются по

А) степеням свободы остаточной дисперсий

Б) степеням свободы факторной дисперсий

*В) уровню значимости и степеням свободы факторной и остаточной дисперсий

 

Вопрос: При оценке статистической значимости построенной эконометрической модели выдвигают ______ гипотезы.

*А) статистические

Б) Математические

В) Вероятностные

 

Вопрос: 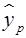это

А) теоретическое значение Y

*Б) прогнозное значение Y

В) частное решение уравнения

 

Вопрос: Если доверительный интервал для параметра проходит через точку ноль, следовательно

*А) параметр является несущественным,

Б) параметр в некоторой точке равен нулю.

В) ничего не означает.

 

Вопрос: Значение коэффициента корреляции равно 0,9. Следовательно, значение коэффициента детерминации составит

А) 0,1,

*Б) 0,81,

В) 99,1.

 

Вопрос: Исходные данные - представленный в таблице набор n пар чисел (Y, X), где X - независимая переменная, а Y - зависимая. Предполагается, что переменные связаны зависимостью Y_k = bX_k + a + ε_k , k = 1,2,...,n, где a и b - параметры, неизвестные статистику и подлежащие оцениванию, а ε_k - погрешности, искажающие зависимость. n = 6.

Xk
Yk

Оценка коэффициента b, полученная методом наименьших квадратов, есть ……………..

А) 3.33

*Б) 2.56

В) 7.23

 

Вопрос: Исходные данные - представленный в таблице набор n пар чисел (Y, X), где X - независимая переменная, а Y - зависимая. Предполагается, что переменные связаны зависимостью Y_k = bX_k + a + ε_k , k = 1,2,...,n, где a и b - параметры, неизвестные статистику и подлежащие оцениванию, а ε_k - погрешности, искажающие зависимость. n = 6.

Xk
Yk

Оценка свободного члена a, полученная методом наименьших квадратов, есть…………..

*А) 12.42

Б) 5

В) 12

 

Вопрос: Исходные данные - представленный в таблице набор n пар чисел (Y, X), где X - независимая переменная, а Y - зависимая. Предполагается, что переменные связаны зависимостью Y_k = aX_k + b + ε_k , k = 1,2,...,n, где a и b - параметры, неизвестные статистику и подлежащие оцениванию, а ε_k - погрешности, искажающие зависимость. n = 6.

Xk
Yk

Коэффициент корреляции r_YX равен:………………………….

А) -1

Б) 01

*В) 0.998

 

Вопрос: Исходные данные - представленный в таблице набор n пар чисел (Y, X), где X - независимая переменная, а Y - зависимая. Предполагается, что переменные связаны зависимостью Y_k = bX_k + a + ε_k , k = 1,2,...,n, где a и b - параметры, неизвестные статистику и подлежащие оцениванию, а ε_k - погрешности, искажающие зависимость. n = 6.

Xk
Yk

Критическое значение t-критерия Стьюдента на уровне значимости 0,95 для нашего случая равно 2,776. _{………………………………………}

*А) статистически значим

Б) статистически незначим

В) нельзя ничего сказать

 

Вопрос: Исходные данные - представленный в таблице набор n пар чисел (Y, X), где X - независимая переменная, а Y - зависимая. Предполагается, что переменные связаны зависимостью Y_k = bX_k + a + ε_k , k = 1,2,...,n, где a и b - параметры, неизвестные статистику и подлежащие оцениванию, а ε_k - погрешности, искажающие зависимость. n = 6.

Xk
Yk

Сумма исходных значений зависимой переменной больше суммы восстановленных значений этой переменной на ………………………………………………….

А) 10

*Б) 0

В) 1

 

Вопрос: Исходные данные - представленный в таблице набор n пар чисел (Y, X), где X - независимая переменная, а Y - зависимая. Предполагается, что переменные связаны зависимостью Y_k = bX_k + a + ε_k , k = 1,2,...,n, где a и b - параметры, неизвестные статистику и подлежащие оцениванию, а ε_k - погрешности, искажающие зависимость. n = 6.

Xk
Yk

Остаточная сумма квадратов равна ………………………………………

*А) 1,17

Б) 1,3

В) 0,17

 

Вопрос: Исходные данные - представленный в таблице набор n пар чисел (Y, X), где X - независимая переменная, а Y - зависимая. Предполагается, что переменные связаны зависимостью Y_k = bX_k + a + ε_k , k = 1,2,...,n, где a и b - параметры, неизвестные статистику и подлежащие оцениванию, а ε_k - погрешности, искажающие зависимость. n = 6.

Xk
Yk

Сумма квадратов отклонений восстановленных значений Y от среднего по выборке равна ……………………………………………….

А) 284

Б) 324

*В) 284,33

 

Вопрос: Исходные данные - представленный в таблице набор n пар чисел (Y, X), где X - независимая переменная, а Y - зависимая. Предполагается, что переменные связаны зависимостью Y_k = bX_k + a + ε_k , k = 1,2,...,n, где a и b - параметры, неизвестные статистику и подлежащие оцениванию, а ε_k - погрешности, искажающие зависимость. n = 6..

Xk
Yk

Значение F –критерия Фишера для проверки статистической значимости полученного уравнения регрессии в целом равно ……………………………………………..

А) 256

*Б) 972,71

В) 365

 

Вопрос: Исходные данные - представленный в таблице набор n пар чисел (Y, X), где X - независимая переменная, а Y - зависимая. Предполагается, что переменные связаны зависимостью Y_k = bX_k + a + ε_k , k = 1,2,...,n, где a и b - параметры, неизвестные статистику и подлежащие оцениванию, а ε_k - погрешности, искажающие зависимость. n = 6..

Xk
Yk

Критическое значение F-критерия Фишера на уровне значимости 0,95 для нашего случая равно 7,71. Полученное уравнение в целом ………………………………………………….

*А) статистически значимо

Б) статистически ненадежное

В) нельзя ничего сказать

 

Вопрос: Исходные данные - представленный в таблице набор n пар чисел (Y, X), где X - независимая переменная, а Y - зависимая. Предполагается, что переменные связаны зависимостью Y_k = bX_k + a + ε_k , k = 1,2,...,n, где a и b - параметры, неизвестные статистику и подлежащие оцениванию, а ε_k - погрешности, искажающие зависимость. n = 6.

Xk
Yk

Коэффициент эластичности переменной Y по переменной X равен ……………………………..

А) 0,5

*Б) 0,579

В) 0,421

 

Вопрос: Исходные данные - представленный в таблице набор n пар чисел (Y, X), где X - независимая переменная, а Y - зависимая. Предполагается, что переменные связаны зависимостью Y_k = bX_k + a + ε_k , k = 1,2,...,n, где a и b - параметры, неизвестные статистику и подлежащие оцениванию, а ε_k - погрешности, искажающие зависимость. n = 7.

Xk
Yk

Оценка коэффициента b, полученная методом наименьших квадратов, есть ……………..

А) 3.33

*Б) 2.48

В) 7.23

 

Вопрос: Исходные данные - представленный в таблице набор n пар чисел (Y, X), где X - независимая переменная, а Y - зависимая. Предполагается, что переменные связаны зависимостью Y_k = bX_k + a + ε_k , k = 1,2,...,n, где a и b - параметры, неизвестные статистику и подлежащие оцениванию, а ε_k - погрешности, искажающие зависимость. n = 7.

Xk
Yk

Оценка свободного члена a, полученная методом наименьших квадратов, есть…………..

*А) 12.84

Б) 5

В) 12.1

 

Вопрос: Анализ тесноты и направления связей двух признаков осуществляется на основе:

*А) парного коэффициента корреляции;

Б) коэффициента детерминации;

В) множественного коэффициента корреляции.

 

Вопрос: Какой показатель используется для определения части вариации, обусловленной изменением величины изучаемого фактора?

а) коэффициент вариации;

б) коэффициент корреляции;

*в) коэффициент детерминации;

г) коэффициент эластичности.

 

Вопрос: Коэффициент эластичности показывает:

*А) на сколько % изменится значение y при изменении x на 1 %;

Б) на сколько единиц своего измерения изменится значение y при изменении x на 1 %;

В) на сколько % изменится значение y при изменении x на ед. своего измерения.

 

Вопрос: В каких пределах меняется коэффициент детерминации?

А) от 0 до + ;

Б) от - до + ;

*В) от 0 до +1;

Г) от -l до +1.

 

Вопрос: Какие показатели по своей величине существуют в пределах от минус до плюс единицы:

А) коэффициент детерминации;

Б) коэффициент корреляции и детерминации;

*В) линейный коэффициент корреляции.

 

Вопрос: Коэффициент регрессии при однофакторной модели показывает:

*А) на сколько единиц изменяется функция при изменении аргумента на одну единицу;

Б) на сколько процентов изменяется функция на одну единицу изменения аргумента.

 

Вопрос: Величина индекса корреляции, равная 1,587, свидетельствует:

А) о слабой их зависимости;

Б) о сильной взаимосвязи;

*В) об ошибках в вычислениях.

 

Вопрос: Величина коэффициента корреляции, равная 0,87, свидетельствует:

А) о слабой их зависимости;

*Б) о сильной взаимосвязи;

В) об ошибках в вычислениях.

 

Вопрос: Величина коэффициента корреляции, равная 0,087, свидетельствует:

*А) о слабой их зависимости;

Б) о сильной взаимосвязи;

В) об ошибках в вычислениях.

 

Вопрос: Величина коэффициента корреляции, равная -1,00, свидетельствует:

*А) о слабой их зависимости;

Б) о сильной взаимосвязи;

В) об ошибках в вычислениях.

 

Вопрос: Модель линейной парной регрессии имеет вид y=-5.79+36.84x, коэффициент регрессии в такой модели равен:

А)5,79

Б)0

*В) 36.84.

 

Вопрос: Модель линейной парной регрессии имеет вид y=1.9+0.65x, коэффициент регрессии в такой модели равен:

А)1,9

*Б)0,65

В)1

 

Вопрос: Модель линейной парной регрессии имеет вид y=3.4+2.986x, коэффициент регрессии в такой модели равен:

*А) 2.986

Б)3,4

В)0

 

Вопрос: Метод наименьших квадратов может применяться в случае

А) линейной регрессии

*Б) нелинейной и линейной множественной регрессии

В) нелинейной регрессии

 

Вопрос: Модель линейной парной регрессии имеет вид y=-6-36.84x, коэффициент регрессии в такой модели равен:

А)6

Б)36,84

*В) -36.84

 

Вопрос: Модель линейной парной регрессии имеет вид y=0.65+1.9x, коэффициент регрессии в такой модели равен:

А) 0.65

*Б)1,9

В)1

 

Вопрос: Модель линейной парной регрессии имеет вид y=2.986-3.4x, коэффициент регрессии в такой модели равен:

А) 2.986

Б)-3,4

В)3,4

 

Вопрос: Математическая форма записи уравнения зависимости переменной у от одного или нескольких факторов х называется ______ эконометрической модели.

*А) спецификацией

Б) верификацией

 

Вопрос: Метод наименьших квадратов применим к уравнениям регрессии, …

А) которые могут представлены любой функцией

*Б) которые отражают линейную зависимость между двумя экономическими показателями

 

Вопрос: Корреляционная связь между переменными X и Y считается тесной, если коэффициент корреляции принимает следующие значения:

А) 0<r_xy<1

Б) -0.7<r_xy<1

*В) 0.7<r_xy<1

 

Вопрос: Корреляционная связь между переменными X и Y считается умеренной, если коэффициент корреляции принимает следующие значения:

А) 0.7<r_xy<1

*Б) 0.3<r_xy<0.7

В) 0<r_xy<1

 

Вопрос: Корреляционная связь между переменными X и Y считается слабой, если коэффициент корреляции принимает следующие значения:

А) -0.7<r_xy<0

*Б) 0<r_xy<0.3

В) 0<r_xy<1

 

Вопрос: Корреляционная связь между переменными X и Y считается линейной функциональной, если коэффициент корреляции принимает следующие значения:

*А) r_xy=1

Б0<r_xy<1

В) r_xy=0

 

Вопрос: Коэффициент детерминации R является показателем

*А) качества построенной модели

Б) тесноты линейной связи

В) значимости уравнения регрессии

 

Вопрос: Коэффициент детерминации рассчитывается для оценки качества

*А) подбора уравнения регрессии

Б)

В)

 

Вопрос: Коэффициент детерминации для модели линейной парной регрессии может быть рассчитан по формуле:

А) R=(r_xy)³

Б) R=(r_xy)^1/2

*В) R=(r_xy)²