 |
Главная |
Тема: Множественная линейная регрессия
|
из
5.00
|
Вопрос: Множественная регрессия— это
*А) регрессия с двумя и более факторными переменными;
Б) с одним фактором;
Вопрос: Факторы эконометрической модели являются коллинеарными, если коэффициент корреляции между ними по модулю больше
А) 0,5;
Б) 1;
*В) 0,7.
Вопрос: Добавление в уравнение множественной регрессии новой объясняющей переменной:
*А) никогда не уменьшает значение коэффициента детерминации;
Б) не оказывает никакого влияние на коэффициент детерминации.
В) увеличивает значение коэффициента детерминации;
Вопрос: Скорректированный коэффициент детерминации:
*А) меньше обычного коэффициента детерминации;
Б) больше обычного коэффициента детерминации;
В) меньше или равен обычному коэффициенту детерминации;
Вопрос: С увеличением числа объясняющих переменных скорректированный коэффициент детерминации:
А) увеличивается;
*Б) уменьшается;
В) не изменяется.
Вопрос: Если коэффициент детерминации, равен нулю то критерий Фишера равен:
*А) нулю;
Б) единице;
В) больше или равен единице.
Вопрос: Число степеней свободы для остаточной суммы квадратов в линейной модели множественной регрессии равно:
А) 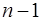 ;
;
Б) 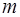 ;
;
*В) 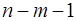 .
.
Вопрос: Число степеней свободы для общей суммы квадратов в линейной модели множественной регрессии равно:
*А) 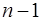 ;
;
Б) 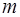 ;
;
В) 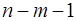 .
.
Вопрос: Число степеней свободы для факторной суммы квадратов в линейной модели множественной регрессии равно:
А) 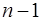 ;
;
*Б) 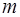 ;
;
В) 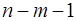 .
.
Вопрос: Множественный коэффициент корреляции 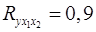 . Определите, какой процент дисперсии зависимой переменной
. Определите, какой процент дисперсии зависимой переменной  объясняется влиянием факторов
объясняется влиянием факторов 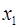 и
и 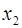 :
:
*А) 90%;
Б) 81%;
В) 19%.
Вопрос: Для построения модели линейной множественной регрессии вида 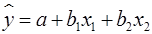 необходимое количество наблюдений должно быть не менее:
необходимое количество наблюдений должно быть не менее:
А) 2;
Б) 7;
*В) 14.
Вопрос: Стандартизованные коэффициенты регрессии 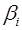 :
:
*А) позволяют ранжировать факторы по силе их влияния на результат;
Б) оценивают статистическую значимость факторов;
В) являются коэффициентами эластичности.
Вопрос: Частные коэффициенты корреляции
А) характеризуют тесноту связи рассматриваемого набора факторов с исследуемым признаком;
Б) содержат поправку на число степеней свободы и не допускают преувеличения тесноты связи;
*В) характеризуют тесноту связи между результатом и соответствующим фактором при элиминировании других факторов, включенных в уравнение регрессии.
Вопрос: Частный  -критерий:
-критерий:
А) оценивает значимость уравнения регрессии в целом;
*Б) служит мерой для оценки включения фактора в модель;
В) ранжирует факторы по силе их влияния на результат.
Вопрос: Состоятельность оценки параметра регрессии, полученной по МНК, означает:
А) что она характеризуется наименьшей дисперсией;
Б) что математическое ожидание остатков равно нулю;
В) увеличение ее точности с увеличением объема выборки.
Вопрос: Укажите истинное утверждение:
А) скорректированный и обычный коэффициенты множественной детерминации совпадают только в тех случаях, когда обычный коэффициент множественной детерминации равен нулю;
*Б) стандартные ошибки коэффициентов регрессии определяются значениями всех параметров регрессии;
В) при наличии гетероскедастичности оценки параметров регрессии становятся смещенными.
Вопрос: При наличии гетероскедастичности следует применять:
А) обычный МНК;
*Б) обобщенный МНК;
В) метод максимального правдоподобия.
Вопрос: Фиктивные переменные – это:
*А) атрибутивные признаки (например, как профессия, пол, образование), которым придали цифровые метки;
Б) экономические переменные, принимающие количественные значения в некотором интервале;
В) значения зависимой переменной за предшествующий период времени.
Вопрос: По 20 наблюдениям построено уравнение регрессии: 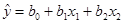 . Для проверки значимости уравнения вычислено значение t статистики: 4.2. Выводы:
. Для проверки значимости уравнения вычислено значение t статистики: 4.2. Выводы:
*А) Уравнение значимо при a=0.05;
Б) Уравнение незначимо при a=0.1;
В) Уравнение незначимо при a=0.01.
Вопрос: По 23 наблюдениям построено уравнение регрессии: 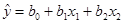 . Для проверки значимости уравнения вычислено значение t статистики: 2.5 Выводы:
. Для проверки значимости уравнения вычислено значение t статистики: 2.5 Выводы:
*А) Уравнение значимо при a=0.05;
Б) Уравнение незначимо при a=0.1;
В) Уравнение значимо при a=0.01.
Вопрос: По 24 наблюдениям построено уравнение регрессии: 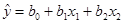 . Для проверки значимости уравнения вычислено значение t статистики: 2.4 Выводы:
. Для проверки значимости уравнения вычислено значение t статистики: 2.4 Выводы:
А) Уравнение незначимо при a=0.05;
Б) Уравнение незначимо при a=0.1;
*В) Уравнение незначимо при a=0.01.
Вопрос: По 26 наблюдениям построено уравнение регрессии: 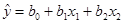 . Для проверки значимости уравнения вычислено значение t статистики: 3 Выводы:
. Для проверки значимости уравнения вычислено значение t статистики: 3 Выводы:
А) Уравнение незначимо при a=0.05;
Б) Уравнение незначимо при a=0.1;
*В) Уравнение значимо при a=0.01.
.
Вопрос: Построено уравнение множественной регрессии 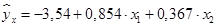 . Чему равен свободный член
. Чему равен свободный член
*А)-3,54
Б)0,854
В)0,376
Вопрос: Построено уравнение множественной регрессии 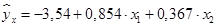 . Чему равен параметр b1
. Чему равен параметр b1
А)-3,54
*Б)0,854
В)0,376
Вопрос: Построено уравнение множественной регрессии 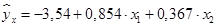 . Чему параметр b2
. Чему параметр b2
А)-3,54
Б)0,854
*В)0,376
Вопрос: Построено стандартизированное уравнение регрессии 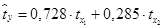 . Чему равен стандартизированный коэффициент β1
. Чему равен стандартизированный коэффициент β1
*А)0,728
Б)0,285
Вопрос: Построено стандартизированное уравнение регрессии 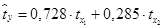 . Чему равен стандартизированный коэффициент β2
. Чему равен стандартизированный коэффициент β2
А)0,728
*Б)0,285
Вопрос: Построено стандартизированное уравнение регрессии 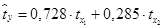 . Выберите наиболее значимый стандартизированный коэффициент
. Выберите наиболее значимый стандартизированный коэффициент
*А)0,728
Б)0,285
Вопрос: Построено стандартизированное уравнение регрессии 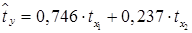 Чему равен стандартизированный коэффициент β2
Чему равен стандартизированный коэффициент β2
А)0,746
*Б)0,237
Вопрос: Построено стандартизированное уравнение регрессии 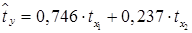 Выберите наиболее значимый стандартизированный коэффициент
Выберите наиболее значимый стандартизированный коэффициент
*А)0,746
Б)0,237
Вопрос: Построено стандартизированное уравнение регрессии 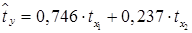 Чему равен стандартизированный коэффициент β1
Чему равен стандартизированный коэффициент β1
*А)0,746
Б)0,237
Вопрос: Найдены коэффициенты парной корреляции 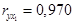 ;
; 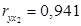 ;
; 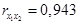 . Они указывают
. Они указывают
*А) На весьма сильную связь каждого фактора с результатом, а также межфакторную зависимость
Б) Ничего определенного сказать нельзя
В) Связь отсутсвует
Вопрос: В множественном линейном уравнении регрессии строятся доверительные интервалы для коэффициентов регрессии с помощью распределения:
А) Нормального;
*Б) Стьюдента;
В) Фишера-Снедекора.
Вопрос: Значение в линейной модели коэффициента детерминации R2 изменяется:
*А) [0,1];
Б) [0,1);
В) [-1, 1].
Вопрос: Множественный коэффициент корреляции равен 0.81. Какой процент дисперсии результативного признака объясняется влиянием всех факторных признаков?
А) 90 %;
*Б) 81 %;
В) 95 %;
Вопрос: В каких пределах меняется множественный коэффициент корреляции?
А) от -  до +
до +  ;
;
Б) от 0 до 1;
*В) от –1 до +1.
Вопрос: При добавлении в уравнение регрессии еще одного объясняющего фактора коэффициент детерминации:
А) уменьшится;
*Б) возрастет;
В) сохранит свое значение;
Г) не уменьшится.
Вопрос: Модель в целом статистически значима, если:
А) Fрасч. < Fтабл .
Б) ç Fрасч. ç< Fтабл .
*В) Fрасч. > Fтабл .
Г) Fрасч. = Fтабл .
Д) Fрасч≠Fтабл .
Вопрос: Строится линейная регрессионная модель переменной Y по переменным X1 и X2:
Yk = a0 + a1X1k + a2X2k + εk , k = 1,2,…,n, где a0 , a1 и a2 – параметры, неизвестные статистику и подлежащие оцениванию, а  εk – погрешности, искажающие зависимость. Количество наблюдений n = 8. Средние значения, вычисленные по выборке:
εk – погрешности, искажающие зависимость. Количество наблюдений n = 8. Средние значения, вычисленные по выборке: 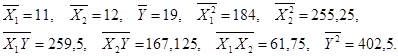
Матрица парных коэффициентов корреляции:
| Y | X1 | X2 | |
| Y | 0,988 | -0,896 | |
| X1 | 0,988 | -0,839 | |
| X2 | -0,896 | -0,839 |
Критическое значение F-критерия Фишера 5,79. Критическое значение t-критерия Стьюдента 2,571. Оценка коэффициента a0, полученная методом наименьших квадратов, есть: ………………………………………………………………….
А) 13,05
*Б) 13,55
В) 1,55
Вопрос: Строится линейная регрессионная модель переменной Y по переменным X1 и X2:
Yk = a0 + a1X1k + a2X2k + εk , k = 1,2,…,n, где a0 , a1 и a2 – параметры, неизвестные статистику и подлежащие оцениванию, а  εk – погрешности, искажающие зависимость. Количество наблюдений n = 8. Средние значения, вычисленные по выборке:
εk – погрешности, искажающие зависимость. Количество наблюдений n = 8. Средние значения, вычисленные по выборке: 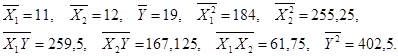
Матрица парных коэффициентов корреляции:
| Y | X1 | X2 | |
| Y | 0,988 | -0,896 | |
| X1 | 0,988 | -0,839 | |
| X2 | -0,896 | -0,839 |
Критическое значение F-критерия Фишера 5,79. Критическое значение t-критерия Стьюдента 2,571. Оценка коэффициента a1, полученная методом наименьших квадратов, есть ………………………………………………………………………..
*А) 0,65
Б) 1
В) 0,35
Вопрос:
Строится линейная регрессионная модель переменной Y по переменным X1 и X2:
Yk = a0 + a1X1k + a2X2k + εk , k = 1,2,...,n, где a0 , a1 и a2 - параметры, неизвестные статистику и подлежащие оцениванию, а  εk - погрешности, искажающие зависимость. Количество наблюдений n = 8. Средние значения, вычисленные по выборке:
εk - погрешности, искажающие зависимость. Количество наблюдений n = 8. Средние значения, вычисленные по выборке: 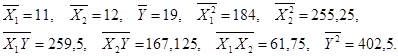
Матрица парных коэффициентов корреляции:
| Y | X1 | X2 | |
| Y | 0,988 | -0,896 | |
| X1 | 0,988 | -0,839 | |
| X2 | -0,896 | -0,839 |
Критическое значение F-критерия Фишера 5,79. Критическое значение t-критерия Стьюдента 2,571. Оценка коэффициента a2, полученная методом наименьших квадратов, есть: ………………………………………………………………………….
*А) -0,14
Б) 0,14
В) 0,04
Вопрос : . Строится линейная регрессионная модель переменной Y по переменным X1 и X2:
Yk = a0 + a1X1k + a2X2k + εk , k = 1,2,...,n, где a0 , a1 и a2 - параметры, неизвестные статистику и подлежащие оцениванию, а  εk - погрешности, искажающие зависимость. Количество наблюдений n = 8. Средние значения, вычисленные по выборке:
εk - погрешности, искажающие зависимость. Количество наблюдений n = 8. Средние значения, вычисленные по выборке: 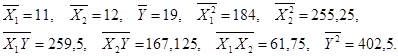
Матрица парных коэффициентов корреляции:
| Y | X1 | X2 | |
| Y | 0,988 | -0,896 | |
| X1 | 0,988 | -0,839 | |
| X2 | -0,896 | -0,839 |
Критическое значение F-критерия Фишера 5,79. Критическое значение t-критерия Стьюдента 2,571. Эластичность переменной Y по переменной X1…………………………………………
*А) 0,37
Б) 0,25
В) 1
Вопрос: Строится линейная регрессионная модель переменной Y по переменным X1 и X2:
Yk = a0 + a1X1k + a2X2k + εk , k = 1,2,...,n, где a0 , a1 и a2 - параметры, неизвестные статистику и подлежащие оцениванию, а  εk - погрешности, искажающие зависимость. Количество наблюдений n = 8. Средние значения, вычисленные по выборке:
εk - погрешности, искажающие зависимость. Количество наблюдений n = 8. Средние значения, вычисленные по выборке: 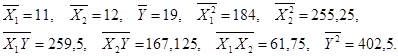
Матрица парных коэффициентов корреляции:
| Y | X1 | X2 | |
| Y | 0,988 | -0,896 | |
| X1 | 0,988 | -0,839 | |
| X2 | -0,896 | -0,839 |
Критическое значение F-критерия Фишера 5,79. Критическое значение t-критерия Стьюдента 2,571. Эластичность переменной Y по переменной X2……………………………………………..
*А) -0,09
Б) 0,01
В) -0,2
Вопрос: Строится линейная регрессионная модель переменной Y по переменным X1 и X2:
Yk = a0 + a1X1k + a2X2k + εk , k = 1,2,...,n, где a0 , a1 и a2 - параметры, неизвестные статистику и подлежащие оцениванию, а  εk - погрешности, искажающие зависимость. Количество наблюдений n = 8. Средние значения, вычисленные по выборке:
εk - погрешности, искажающие зависимость. Количество наблюдений n = 8. Средние значения, вычисленные по выборке: 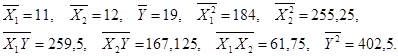
Матрица парных коэффициентов корреляции:
| Y | X1 | X2 | |
| Y | 0,988 | -0,896 | |
| X1 | 0,988 | -0,839 | |
| X2 | -0,896 | -0,839 |
Критическое значение F-критерия Фишера 5,79. Критическое значение t-критерия Стьюдента 2,571. При увеличении переменной X1 на 1 усл. Ед. переменная Y…………………………………………
*А) увеличится на 0,65 усл.ед.
Б) увеличится на 1 усл.ед.
В) увеличится на 65 усл.ед.
Вопрос: Строится линейная регрессионная модель переменной Y по переменным X1 и X2:
Yk = a0 + a1X1k + a2X2k + εk , k = 1,2,...,n, где a0 , a1 и a2 - параметры, неизвестные статистику и подлежащие оцениванию, а  εk - погрешности, искажающие зависимость. Количество наблюдений n = 8. Средние значения, вычисленные по выборке:
εk - погрешности, искажающие зависимость. Количество наблюдений n = 8. Средние значения, вычисленные по выборке: 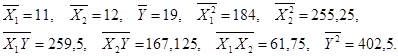
Матрица парных коэффициентов корреляции:
| Y | X1 | X2 | |
| Y | 0,988 | -0,896 | |
| X1 | 0,988 | -0,839 | |
| X2 | -0,896 | -0,839 |
Критическое значение F-критерия Фишера 5,79. Критическое значение t-критерия Стьюдента 2,571. При увеличении переменной X2 на 1 усл. Ед. переменная Y………………………………………
*А) уменьшится на 0,14 усл.ед.
Б) увеличится на 0,14 усл.ед
В) уменьшится на 14 усл.ед
Вопрос: Строится линейная регрессионная модель переменной Y по переменным X1 и X2:
Yk = a0 + a1X1k + a2X2k + εk , k = 1,2,...,n, где a0 , a1 и a2 - параметры, неизвестные статистику и подлежащие оцениванию, а  εk - погрешности, искажающие зависимость. Количество наблюдений n = 8. Средние значения, вычисленные по выборке:
εk - погрешности, искажающие зависимость. Количество наблюдений n = 8. Средние значения, вычисленные по выборке: 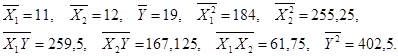
Матрица парных коэффициентов корреляции:
| Y | X1 | X2 | |
| Y | 0,988 | -0,896 | |
| X1 | 0,988 | -0,839 | |
| X2 | -0,896 | -0,839 |
Критическое значение F-критерия Фишера 5,79. Критическое значение t-критерия Стьюдента 2,571. Коэффициент частной корреляции 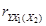 равен …………………………..
равен …………………………..
*А) 0,976
Б) 0,9
В) 0,89
Вопрос: Строится линейная регрессионная модель переменной Y по переменным X1 и X2:
Yk = a0 + a1X1k + a2X2k + εk , k = 1,2,...,n, где a0 , a1 и a2 - параметры, неизвестные статистику и подлежащие оцениванию, а  εk - погрешности, искажающие зависимость. Количество наблюдений n = 8. Средние значения, вычисленные по выборке:
εk - погрешности, искажающие зависимость. Количество наблюдений n = 8. Средние значения, вычисленные по выборке: 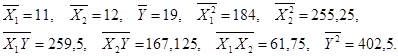
Матрица парных коэффициентов корреляции:
| Y | X1 | X2 | |
| Y | 0,988 | -0,896 | |
| X1 | 0,988 | -0,839 | |
| X2 | -0,896 | -0,839 |
Критическое значение F-критерия Фишера 5,79. Критическое значение t-критерия Стьюдента 2,571. Коэффициент частной корреляции 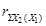 равен ………………………
равен ………………………
*А) -0,788
Б) 0,788
В) 0,88
Вопрос: Строится линейная регрессионная модель переменной Y по переменным X1 и X2:
Yk = a0 + a1X1k + a2X2k + εk , k = 1,2,...,n, где a0 , a1 и a2 - параметры, неизвестные статистику и подлежащие оцениванию, а  εk - погрешности, искажающие зависимость. Количество наблюдений n = 8. Средние значения, вычисленные по выборке:
εk - погрешности, искажающие зависимость. Количество наблюдений n = 8. Средние значения, вычисленные по выборке: 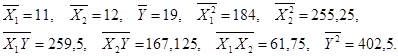
Матрица парных коэффициентов корреляции:
| Y | X1 | X2 | |
| Y | 0,988 | -0,896 | |
| X1 | 0,988 | -0,839 | |
| X2 | -0,896 | -0,839 |
Критическое значение F-критерия Фишера 5,79. Критическое значение t-критерия Стьюдента 2,571.Коэффициент частной корреляции 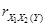 равен ………………………..
равен ………………………..
*А) 0,656
Б) -0,656
В) 1
Вопрос: Строится линейная регрессионная модель переменной Y по переменным X1 и X2:
Yk = a0 + a1X1k + a2X2k + εk , k = 1,2,...,n, где a0 , a1 и a2 - параметры, неизвестные статистику и подлежащие оцениванию, а  εk - погрешности, искажающие зависимость. Количество наблюдений n = 8. Средние значения, вычисленные по выборке:
εk - погрешности, искажающие зависимость. Количество наблюдений n = 8. Средние значения, вычисленные по выборке: 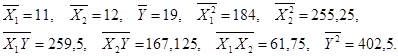
Матрица парных коэффициентов корреляции:
| Y | X1 | X2 | |
| Y | 0,988 | -0,896 | |
| X1 | 0,988 | -0,839 | |
| X2 | -0,896 | -0,839 |
Критическое значение F-критерия Фишера 5,79. Критическое значение t-критерия Стьюдента 2,571.Множественный коэффициент корреляции 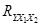 ………………………..
………………………..
*А) 0,995
Б) -0,995
В) 1
Вопрос: Строится линейная регрессионная модель переменной Y по переменным X1 и X2:
Yk = a0 + a1X1k + a2X2k + εk , k = 1,2,...,n, где a0 , a1 и a2 - параметры, неизвестные статистику и подлежащие оцениванию, а  εk - погрешности, искажающие зависимость. Количество наблюдений n = 8. Средние значения, вычисленные по выборке:
εk - погрешности, искажающие зависимость. Количество наблюдений n = 8. Средние значения, вычисленные по выборке: 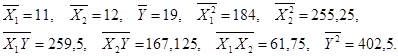
Матрица парных коэффициентов корреляции:
| Y | X1 | X2 | |
| Y | 0,988 | -0,896 | |
| X1 | 0,988 | -0,839 | |
| X2 | -0,896 | -0,839 |
Критическое значение F-критерия Фишера 5,79. Критическое значение t-критерия Стьюдента 2,571. Скорректированный коэффициент детерминации …………………..
*А) 0,985
Б) -0,985
В) 0
Вопрос: Строится линейная регрессионная модель переменной Y по переменным X1 и X2:
Yk = a0 + a1X1k + a2X2k + εk , k = 1,2,...,n, где a0 , a1 и a2 - параметры, неизвестные статистику и подлежащие оцениванию, а  εk - погрешности, искажающие зависимость. Количество наблюдений n = 8. Средние значения, вычисленные по выборке:
εk - погрешности, искажающие зависимость. Количество наблюдений n = 8. Средние значения, вычисленные по выборке: 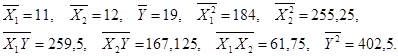
Матрица парных коэффициентов корреляции:
| Y | X1 | X2 | |
| Y | 0,988 | -0,896 | |
| X1 | 0,988 | -0,839 | |
| X2 | -0,896 | -0,839 |
Критическое значение F-критерия Фишера 5,79. Критическое значение t-критерия Стьюдента 2,571. Коэффициент частной корреляции 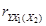 ……………………………….
……………………………….
*А) статистически значим
Б) статистически незначим
Вопрос: Строится линейная регрессионная модель переменной Y по переменным X1 и X2:
Yk = a0 + a1X1k + a2X2k + εk , k = 1,2,...,n, где a0 , a1 и a2 - параметры, неизвестные статистику и подлежащие оцениванию, а  εk - погрешности, искажающие зависимость. Количество наблюдений n = 8. Средние значения, вычисленные по выборке:
εk - погрешности, искажающие зависимость. Количество наблюдений n = 8. Средние значения, вычисленные по выборке: 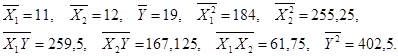
Матрица парных коэффициентов корреляции:
| Y | X1 | X2 | |
| Y | 0,988 | -0,896 | |
| X1 | 0,988 | -0,839 | |
| X2 | -0,896 | -0,839 |
Критическое значение F-критерия Фишера 5,79. Критическое значение t-критерия Стьюдента 2,571. Коэффициент частной корреляции 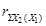 ……………………………….
……………………………….
*А) статистически значим
Б) статистически незначим
Вопрос: Строится линейная регрессионная модель переменной Y по переменным X1 и X2:
Yk = a0 + a1X1k + a2X2k + εk , k = 1,2,...,n, где a0 , a1 и a2 - параметры, неизвестные статистику и подлежащие оцениванию, а  εk - погрешности, искажающие зависимость. Количество наблюдений n = 8. Средние значения, вычисленные по выборке:
εk - погрешности, искажающие зависимость. Количество наблюдений n = 8. Средние значения, вычисленные по выборке: 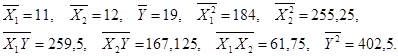
Матрица парных коэффициентов корреляции:
| Y | X1 | X2 | |
| Y | 0,988 | -0,896 | |
| X1 | 0,988 | -0,839 | |
| X2 | -0,896 | -0,839 |
Критическое значение F-критерия Фишера 5,79. Критическое значение t-критерия Стьюдента 2,571.Коэффициент частной корреляции 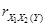 ………………………………….
………………………………….
*А) статистически незначим
Б) статистически незначим
Вопрос: Строится линейная регрессионная модель переменной Y по переменным X1 и X2:
Yk = a0 + a1X1k + a2X2k + εk , k = 1,2,...,n, где a0 , a1 и a2 - параметры, неизвестные статистику и подлежащие оцениванию, а  εk - погрешности, искажающие зависимость. Количество наблюдений n = 8. Средние значения, вычисленные по выборке:
εk - погрешности, искажающие зависимость. Количество наблюдений n = 8. Средние значения, вычисленные по выборке: 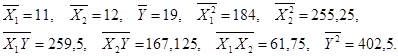
Матрица парных коэффициентов корреляции:
| Y | X1 | X2 | |
| Y | 0,988 | -0,896 | |
| X1 | 0,988 | -0,839 | |
| X2 | -0,896 | -0,839 |
Критическое значение F-критерия Фишера 5,79. Критическое значение t-критерия Стьюдента 2,571. Остаточная сумма квадратов равна ………………………………………..
*А) 3,1
Б) -3,1
В) 0
Вопрос: Строится линейная регрессионная модель переменной Y по переменным X1 и X2:
Yk = a0 + a1X1k + a2X2k + εk , k = 1,2,...,n, где a0 , a1 и a2 - параметры, неизвестные статистику и подлежащие оцениванию, а  εk - погрешности, искажающие зависимость. Количество наблюдений n = 8. Средние значения, вычисленные по выборке:
εk - погрешности, искажающие зависимость. Количество наблюдений n = 8. Средние значения, вычисленные по выборке: 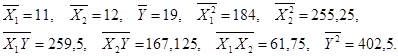
Матрица парных коэффициентов корреляции:
| Y | X1 | X2 | |
| Y | 0,988 | -0,896 | |
| X1 | 0,988 | -0,839 | |
| X2 | -0,896 | -0,839 |
Критическое значение F-критерия Фишера 5,79. Критическое значение t-критерия Стьюдента 2,571. Сумма случайных отклонений равна …………………………………….
*А) 0
Б) 2
В) 1
Вопрос: Строится линейная регрессионная модель переменной Y по переменным X1 и X2:
Yk = a0 + a1X1k + a2X2k + εk , k = 1,2,...,n, где a0 , a1 и a2 - параметры, неизвестные статистику и подлежащие оцениванию, а  εk - погрешности, искажающие зависимость. Количество наблюдений n = 8. Средние значения, вычисленные по выборке:
εk - погрешности, искажающие зависимость. Количество наблюдений n = 8. Средние значения, вычисленные по выборке: 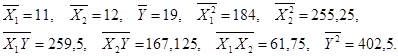
Матрица парных коэффициентов корреляции:
| Y | X1 | X2 | |
| Y | 0,988 | -0,896 | |
| X1 | 0,988 | -0,839 | |
| X2 | -0,896 | -0,839 |
Критическое значение F-критерия Фишера 5,79. Критическое значение t-критерия Стьюдента 2,571. Сумма квадратов отклонений восстановленных значений Y от среднего по выборке равна ……………………………………………………………………………….
*А) 328,9
Б) -3,28
В) 3,28
Вопрос: Строится линейная регрессионная модель переменной Y по переменным X1 и X2:
Yk = a0 + a1X1k + a2X2k + εk , k = 1,2,...,n, где a0 , a1 и a2 - параметры, неизвестные статистику и подлежащие оцениванию, а  εk - погрешности, искажающие зависимость. Количество наблюдений n = 8. Средние значения, вычисленные по выборке:
εk - погрешности, искажающие зависимость. Количество наблюдений n = 8. Средние значения, вычисленные по выборке: 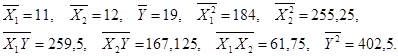
Матрица парных коэффициентов корреляции:
| Y | X1 | X2 | |
| Y | 0,988 | -0,896 | |
| X1 | 0,988 | -0,839 | |
| X2 | -0,896 | -0,839 |
Критическое значение F-критерия Фишера 5,79. Критическое значение t-критерия Стьюдента 2,571. Полученное уравнение в целом по F-критерию Фишера ………………..
А) статистически значимо
Б) статистически незначимо
Вопрос: Построено уравнение регрессии 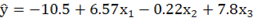 , показывает что
, показывает что
*А) рост переменной x2 на единицу своего измерения приводит к уменьшению среднего значения y на 0,22 единиц своего измерения
Б) рост переменной x2 на 1% приводит к росту среднего значения y на 0,22%
В) рост переменной x2 на единицу своего измерения приводит к росту среднего значения y на 0,22 единиц своего измерения
Вопрос: С увеличением объема выборки:
А) расширяются интервальные оценки
Б) уменьшается ошибка регрессии
*В) увеличивается точность оценок
Г) уменьшается коэффициент детерминации
Вопрос: Число степеней свободы k1 при расчете F-критерия для случая множественной регрессии равно:
А) n, где n – число наблюдений
*Б) k, где k - количество независимых переменных 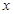
В) n – k
Г) n – (k + 1)
Д) n – (k + 2)
Вопрос: Число степеней свободы k2 при расчете F-критерия для случая множественной регрессии равно:
А) n, где n – число наблюдений
Б) k, где k - количество независимых переменных 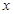
В) n – k
*Г) n – (k + 1)
Д) n – (k + 2)
Вопрос: Число степеней свободы df при расчете t-критерия для случая множественной регрессии равно:
А) n, где n – число наблюдений
Б) k, где k - количество независимых переменных 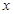
*В) n – k
Г) n – (k + 1)
Д) n – (k + 2)
Вопрос: Уравнение линейной множественной регрессии между зависимой переменной Y и независимой переменной X, где a, b – параметры модели, может иметь вид:
А) Y=a+bX2
*Б) Y=a+b1X1+b2X2
В) Y=a+b1X12+b2X23
Вопрос: Уравнение линейной множественной регрессии между зависимой переменной Y и независимой переменной X, где a, b – параметры модели, не может иметь вид:
*А) Y=a+b1X12+b2X23
Б) Y=a+b1X1+b2X2
Вопрос: Определить коэффициент детерминации линейной двухфакторной модели, если известно, что коэффициент корреляции rxy= -0.5
А) 0
*Б) 0.25
В)-0,25
Вопрос: Определить коэффициент детерминации линейной двухфакторной модели, если известно, что коэффициент корреляции rxy= -0.3
А)-0,09
*Б) 0.09
В)0,9
Вопрос: Определить коэффициент детерминации линейной двухфакторной модели, если известно, что коэффициент корреляции rxy= -0.4
А)-016
Б) 0
*В) 0.16
Вопрос: Определить коэффициент детерминации линейной двухфакторной модели, если известно, что коэффициент корреляции rxy= -0.25
*А) 0.0625
Б)0,8
В)-0,625
Вопрос: Определить коэффициент детерминации линейной двухфакторной модели, если известно, что коэффициент корреляции rxy= -0.6
А)0,63
*Б) 0.36
В)-0,36
Вопрос: Определить коэффициент детерминации линейной двухфакторной модели, если известно, что коэффициент корреляции rxy= -0.7
А)0,5
*Б) 0.49
В)0
Вопрос: Определить коэффициент детерминации линейной двухфакторной модели, если известно, что коэффициент корреляции rxy= 0.7
А)0
Б)0,8
*В) 0.49
Вопрос: Определить коэффициент детерминации линейной двухфакторной модели, если известно, что коэффициент корреляции rxy= 0.8
*А) 0.64
Б)0,6
В)0,5
Вопрос: Определить коэффициент детерминации линейной двухфакторной модели, если известно, что коэффициент корреляции rxy= 0.9
А)0,8
Б)0
*В) 0.81
Вопрос: Определить коэффициент детерминации линейной двухфакторной модели, если известно, что коэффициент корреляции rxy= 0.65
*А) 0.4225
Б)0,4
В)-0,4
Вопрос: Уравнение линейной множественной регрессии между зависимой переменной Y и независимой переменной X, где a, b – параметры модели, может иметь вид:
А) Y=a+bX2
*Б) Y=a+b1X1+b2X2
В) Y=a+b1X12+b2X23
Вопрос: Величина  называется
называется
А) остаток
Б) дисперсия
*В) случайной составляющей
Вопрос: В модели вида 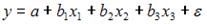 количество объясняющих переменных равно
количество объясняющих переменных равно
А)1
*Б) 3
В)2
Вопрос: В модели множественной регрессии 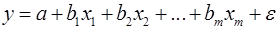 количество объясняющих переменных равно
количество объясняющих переменных равно
*А) m,
Б) 2,
В) m-1.
Вопрос: В модели множественной регрессии 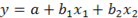
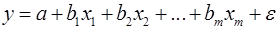 количество объясняющих переменных равно
количество объясняющих переменных равно
А) m,
*Б) 2,
В) m-1.
Вопрос: В модели множественной регрессии 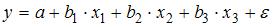 определитель матрицы парных коэффициентов корреляции между факторами
определитель матрицы парных коэффициентов корреляции между факторами 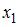 ,
, 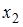 и
и 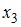 близок к нулю. Это означает, что факторы
близок к нулю. Это означает, что факторы 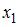 ,
, 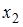 и
и 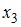 …
…
*А) мультиколлинеарны
Б) один из них равен нулю
В) равны нулю
Вопрос: В уравнении линейной множественной регрессии: 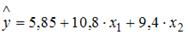 , где
, где 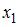 – стоимость основных фондов (тыс. руб.);
– стоимость основных фондов (тыс. руб.); 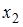 – численность занятых (тыс. чел.); y – объем промышленного производства (тыс. руб.) параметр при переменной х1, равный 10,8, означает, что при увеличении объема основных фондов на _____ объем промышленного производства _____ при постоянной численности занятых.
– численность занятых (тыс. чел.); y – объем промышленного производства (тыс. руб.) параметр при переменной х1, равный 10,8, означает, что при увеличении объема основных фондов на _____ объем промышленного производства _____ при постоянной численности занятых.
*А) на 1 тыс. руб. … увеличится на 10,8 тыс. руб.
Б) на 1 тыс. руб. … увеличится на 0,108 тыс. руб.
В) на 1 тыс. руб. … увеличится на 10,8 %.
Вопрос: В эконометрической модели линейного уравнения регрессии
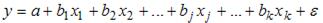 коэффициентом регрессии, характеризующим среднее изменение зависимой переменной при изменении независимой переменной на 1 единицу измерения, является
коэффициентом регрессии, характеризующим среднее изменение зависимой переменной при изменении независимой переменной на 1 единицу измерения, является
*А) bj
Б) a
В) 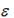
Вопрос: В эконометрической модели линейного уравнения регрессии 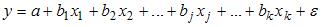 ошибкой модели является …
ошибкой модели является …
А) bj
Б) a
*В) 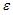
Вопрос: В модели множественной регрессии 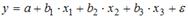 определитель матрицы парных коэффициентов корреляции между факторами
определитель матрицы парных коэффициентов корреляции между факторами 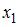 ,
, 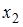 и
и 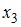 близок к единице. Это означает, что факторы
близок к единице. Это означает, что факторы 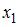 ,
, 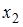 и
и 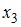 …
…
*А) значимы
Б) мультиколли
|
из
5.00
|
Обсуждение в статье: Тема: Множественная линейная регрессия |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

