 |
Главная |
Тема: Нелинейная регрессия
|
из
5.00
|
Вопрос: Выберите уравнения регрессии, нелинейные относительно объясняющей переменной.
*А) полиномы разных степеней
Б) степенная функция
*В) равносторонняя гипербола
Г) показательная функция
Д) экспоненциальная функция
Вопрос: Выберите уравнения регрессии, нелинейные по оцениваемым параметрам.
А) полиномы разных степеней
*Б) степенная функция
В) равносторонняя гипербола
*Г) показательная функция
*Д) экспоненциальная функция
Вопрос: В уравнении регрессии в форме гиперболы ŷ  если величина b>0, то:
если величина b>0, то:
*А) при увеличении факторного признака х значения результативного признака у замедленно уменьшаются, и при х→∞ средняя величина у будет равна а;
Б) то значение результативного признака у возрастает с замедленным ростом при увеличении факторного признака х, и при х→∞ 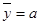
Вопрос: В уравнении регрессии в форме гиперболы ŷ  если величина b<0, то:
если величина b<0, то:
А) при увеличении факторного признака х значения результативного признака у замедленно уменьшаются, и при х→∞ средняя величина у будет равна а;
*Б) то значение результативного признака у возрастает с замедленным ростом при увеличении факторного признака х, и при х→∞ 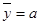
Вопрос: К какому классу нелинейных регрессий относится равносторонняя гипербола:
А) регрессии, нелинейные относительно включенных в анализ переменных, но линейных по оцениваемым параметрам;
*Б) нелинейные регрессии по оцениваемым параметрам.
Вопрос: К какому классу нелинейных регрессий относится парабола:
*А) регрессии, нелинейные относительно включенных в анализ переменных, но линейных по оцениваемым параметрам;
Б) нелинейные регрессии по оцениваемым параметрам.
Вопрос: Коэффициент эластичности определяется по формуле 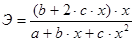 для модели регрессии в форме:
для модели регрессии в форме:
А) Линейной функции;
*Б) Параболы;
В) Гиперболы;
Г) Показательной кривой;
Д) Степенной.
Вопрос: Коэффициент эластичности определяется по формуле 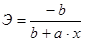 для модели регрессии в форме:
для модели регрессии в форме:
А) Линейной функции;
Б) Параболы;
*В) Гиперболы;
Г) Показательной кривой;
Д) Степенной.
Вопрос: Коэффициент эластичности определяется по формуле 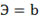 для модели регрессии в форме:
для модели регрессии в форме:
А) Линейной функции;
Б) Параболы;
В) Гиперболы;
Г) Показательной кривой;
*Д) Степенной.
Вопрос: Коэффициент эластичности определяется по формуле 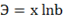 для модели регрессии в форме:
для модели регрессии в форме:
А) Линейной функции;
Б) Параболы;
В) Гиперболы;
*Г) Показательной кривой;
Д) Степенной.
Вопрос: Коэффициент эластичности определяется по формуле 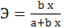 для модели регрессии в форме:
для модели регрессии в форме:
*А) Линейной функции;
Б) Параболы;
В) Гиперболы;
*Г) Показательной кривой;
Д) Степенной.
Вопрос: К какому классу нелинейных регрессий относится показательная кривая:
А) регрессии, нелинейные относительно включенных в анализ переменных, но линейных по оцениваемым параметрам;
*Б) нелинейные регрессии по оцениваемым параметрам.
Вопрос: К какому классу нелинейных регрессий относится степенная кривая:
А) регрессии, нелинейные относительно включенных в анализ переменных, но линейных по оцениваемым параметрам;
*Б) нелинейные регрессии по оцениваемым параметрам.
Вопрос: К какому классу нелинейных регрессий относится экспоненциальная кривая:
А) регрессии, нелинейные относительно включенных в анализ переменных, но линейных по оцениваемым параметрам;
*Б) нелинейные регрессии по оцениваемым параметрам.
Вопрос: К какому классу нелинейных регрессий относится функция вида ŷ 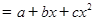 :
:
*А) регрессии, нелинейные относительно включенных в анализ переменных, но линейных по оцениваемым параметрам;
Б) нелинейные регрессии по оцениваемым параметрам.
Вопрос: . К какому классу нелинейных регрессий относится функция вида ŷ  :
:
*А) регрессии, нелинейные относительно включенных в анализ переменных, но линейных по оцениваемым параметрам;
Б) нелинейные регрессии по оцениваемым параметрам.
Вопрос: К какому классу нелинейных регрессий относится функция вида ŷ 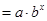 :
:
А) регрессии, нелинейные относительно включенных в анализ переменных, но линейных по оцениваемым параметрам;
*Б) нелинейные регрессии по оцениваемым параметрам.
Вопрос: К какому классу нелинейных регрессий относится функция вида ŷ 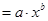 :
:
А) регрессии, нелинейные относительно включенных в анализ переменных, но линейных по оцениваемым параметрам;
*Б) нелинейные регрессии по оцениваемым параметрам.
Вопрос: К какому классу нелинейных регрессий относится функция вида ŷ 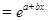 :
:
А) регрессии, нелинейные относительно включенных в анализ переменных, но линейных по оцениваемым параметрам;
*Б) нелинейные регрессии по оцениваемым параметрам.
Вопрос: При помощи какого математического преобразования можно выполнить линеаризацию модели y=a+bx3:
А) путем логарифмирования
*Б) путем замены переменных
Вопрос: При помощи какого математического преобразования можно выполнить линеаризацию модели y=a+b ln x:
А) путем логарифмирования
*Б) путем замены переменных
Вопрос: При помощи какого математического преобразования можно выполнить линеаризацию модели y=a+b/x:
А) путем логарифмирования
*Б) путем замены переменных
Вопрос: При помощи какого математического преобразования можно выполнить линеаризацию модели y=а+bx
*А) путем логарифмирования
Б) путем замены переменных
Вопрос: При помощи какого математического преобразования можно выполнить линеаризацию модели y= а+xb:
*А) путем логарифмирования
Б) путем замены переменных
Вопрос: При помощи какого математического преобразования можно выполнить линеаризацию модели y=а+ebx:
*А) путем логарифмирования
Б) путем замены переменных
Вопрос: Для линеаризации нелинейной регрессионной модели 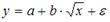 используется замена …
используется замена …
А) 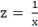
Б) x= ln x, y= ln y
*В) 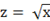
Вопрос: Для линеаризации равносторонней гиперболы используется замена …
*А) 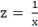
Б) x= ln x, y= ln y
В) 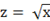
Вопрос: Для линеаризации степенной функции используется замена …
А) 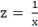
*Б) x= ln x, y= ln y
В) 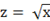
|
из
5.00
|
Обсуждение в статье: Тема: Нелинейная регрессия |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

