Оценка значимости параметров регрессии

При статистической проверке значимости параметров регрессии и коэффициента корреляции в качестве основной гипотезы 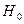выдвигают гипотезу о незначимом отличии от нуля истинного значения параметров регрессии и коэффициента корреляции, т.е. считается что , , . В качестве альтернативной выдвигается обратная гипотеза, т.е. гипотеза, состоящая в том, что значения параметров ненулевые.

Для проверки таких статистических гипотез используется - критерий Стьюдента. Рассмотрим механизм проверки статистической гипотезы:

1) Вычисляют стандартные ошибки параметров по формулам:

или ;

или 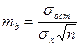; , где

, .

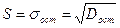2) Используя значения параметров и значения стандартных ошибок, определяют фактические значения - критерия Стьюдента: ; ; .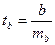

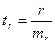3) Определяют табличное (критическое) значение данного параметра, используя заданный уровень значимости и число степеней свободы ( ):

4) Если фактическое значение критерия меньше табличного , то в этом случае нет оснований отвергать основную гипотезу 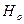и, как следствие, параметр незначимо отличается от нуля при заданном уровне значимости (является статистически незначимым, ненадежным). Если , то нет оснований не отвергнуть (принимать) нулевую гипотезу, следовательно, оцениваемый параметр принимает ненулевое значение, т.е. является статистически значимым, надежным и его можно использовать при прогнозировании.

Для оценки статистической значимости также используются доверительные интервалы:

1. Вычисляют предельные ошибки параметров 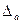, , по формулам:

, , .

2. Находят границы доверительных интервалов:

, , .

3. Если границы доверительного интервала являются противоречивыми (левая отрицательна, правая положительна), то в какой-то момент времени оцениваемый параметр может принимать нулевое значение, следовательно, оцениваемый параметр является статистически незначимым, ненадежным и его нельзя использовать при прогнозировании.

Если границы интервала не противоречивы (обе положительны или обе отрицательны), то параметр считается статистически значимым, надежным.

Замечание

1. Для линейной парной регрессии справедливы следующие формулы:

; ;

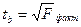2. При использовании - статистики Стьюдента рассматривают абсолютную величину фактического значения данной статистики.

3. Предложенный выше метод оценки статистической надежности коэффициента корреляции справедлив при большом числе наблюдений и в том случае, когда является величиной не близкой к 1. Если величина коэффициента корреляции близка к 1, то вводят вспомогательную величину 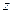: и стандартная ошибка будет равна . Далее критическое значение 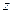- статистики находят из специальных таблиц.