Корреляция для нелинейной регрессии

Составление уравнения нелинейной регрессии дополняется вычислением индекса корреляции

,

где - остаточная дисперсия результативного признака, определяемая исходя из уравнения ;

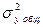- общая дисперсия результативного признака.

Заменив данные дисперсии соответствующими квадратами отклонений, получим

.

Значение индекса корреляции является неотрицательной величиной, заключенной от 0 до 1.

Чем ближе значение к 1, тем теснее связь фактора.

Если после преобразования нелинейной регрессии она принимает форму линейного уравнения парной регрессии, то

, где

- коэффициент линейной корреляции;

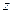- преобразованная величина фактора .

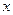Последнее, в частности, является справедливым для уравнения равносторонней гиперболы 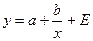и уравнения полулогарифмической регрессии .

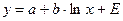Иначе обстоит дело, когда преобразование в линейное уравнение связано с зависимой переменной . В этом случае значение коэффициента регрессии дает приближенное значение тесноты связи исходных факторов и численно не совпадает с индексом нелинейной корреляции . Это справедливо для уравнения степенной показательной регрессии, так как вычисление 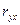происходит по значениям логарифмов фактора, а вычисление происходит по значениям исходных факторов.

Квадрат индекса корреляции для нелинейной регрессии называют индексом детерминации .

.

Экономическая интерпретация индекса детерминации совпадает с экономической интерпретацией коэффициента детерминации.

Значение индекса детерминации используется для вычисления фактического значения F – критерия Фишера

, где

- число наблюдений;

- число параметров при переменной два (число степеней свободы для факторной суммы).

- число степеней свободы для остаточной суммы квадратов отклонений.

Проверка статистической гипотезы о значимости уравнения нелинейной регрессии в целом с помощью F – критерия Фишера производится аналогично оценке статистической значимости уравнения линейной регрессии.

Только критические значения F – критерия определяются следующими условиями

.

Если величина разности индекса и коэффициента детерминации не превосходит 0,1, то предположение о существовании линейной связи фактора считается оправданным. В противном случае, производится оценка существенности различия между и 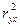с помощью - критерия Стьюдента.

Если полученное фактическое значение окажется меньше 2, то различие между величинами является несущественным.

Тема 10. Множественная регрессия и корреляция.