 |
Главная |
Тема 11. Оценка параметров уравнения множественной регрессии
|
из
5.00
|
Пусть требуется оценить параметры линейной множественной регрессии, т.е. построить линейное уравнение множественной регрессии  .
.
Параметры такого уравнения можно оценить с помощью МНК. При этом необходимо проверить выполнение следующих предпосылок МНК:
1) математическое ожидание случайного отклонения 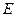 должно быть равно 0 для всех наблюдений;
должно быть равно 0 для всех наблюдений;
2) должно выполняться свойство гомоспедантичности остатков, т.е. постоянство дисперсий отклонений;
3) отсутствие автокорреляции;
4) случайное отклонение должно быть независимо от объясняющих переменных;
5) модель должна быть линейной относительно параметров;
6) отсутствие мультиколлениарности факторов;
7) ошибки 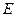 для каждого измерения должны иметь нормальное распределение.
для каждого измерения должны иметь нормальное распределение.
В этом случае система нормальных уравнений для определения параметров множественной регрессии примет вид:

решение которой может быть выполнено с помощью метода определителей
 ;
;  ; …;
; …;  ,
,
где определитель системы нормальных уравнений  ,
, 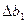 ,
,  - частные определители, получаемые из определителей системы путем замены соответствующего столбца столбцом свободным членом.
- частные определители, получаемые из определителей системы путем замены соответствующего столбца столбцом свободным членом.
Линейное уравнение множественной регрессии может быть представлено в матричной форме:
 , где
, где
 ,
, 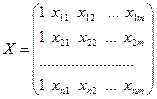 ,
,  ,
,
 -
-  -мерный вектор-столбец значений результативного признака;
-мерный вектор-столбец значений результативного признака;
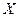 - матрица размерности
- матрица размерности  , представляющая собой наблюдаемые значения факторов
, представляющая собой наблюдаемые значения факторов  ;
;
 - вектор-столбец параметров уравнения регрессии.
- вектор-столбец параметров уравнения регрессии.
В матричной форме решение уравнения можно записать  .
.
Уравнение множественной регрессии вида 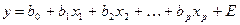 называют уравнением множественной регрессии в натуральном масштабе.
называют уравнением множественной регрессии в натуральном масштабе.
Уравнение множественной регрессии может быть представлено в стандартизированном масштабе  , где
, где  - называются стандартизированными переменными, которые вычисляются по формулам
- называются стандартизированными переменными, которые вычисляются по формулам
 ;
;  .
.
При таком определении стандартизированных переменных их средние значения равны 0, т.е.  , а средние квадратические отклонения – 1, т.е.
, а средние квадратические отклонения – 1, т.е.  .
.
Коэффициенты  называются стандартизированными коэффициентами множественной регрессии.
называются стандартизированными коэффициентами множественной регрессии.
Применяя МНК к уравнению множественной регрессии в стандартизированном масштабе после преобразований получают следующую систему нормальных уравнений:
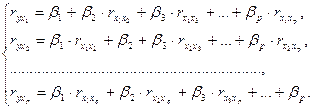
решая которую находим значение стандартизованных коэффициентов  .
.
При составлении системы уравнений использовались следующие коэффициенты парной корреляции  и
и 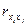 , причем коэффициенты
, причем коэффициенты 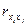 называются коэффициентами межфакторной связи.
называются коэффициентами межфакторной связи.
Коэффициенты парной корреляции можно найти аналогично по формулам для определения коэффициентов корреляции линейной парной регрессии.

Стандартизованные коэффициенты множественной регрессии показывают насколько  изменится в среднем результат при изменении соответствующего фактора
изменится в среднем результат при изменении соответствующего фактора 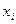 на
на  , при изменении уровня остальных факторов. В силу того, что при составлении уравнения множественной регрессии в стандартизованном масштабе все переменные заданы как централизованные и нормированные стандартизованные коэффициенты
, при изменении уровня остальных факторов. В силу того, что при составлении уравнения множественной регрессии в стандартизованном масштабе все переменные заданы как централизованные и нормированные стандартизованные коэффициенты  сравнимы между собой.
сравнимы между собой.
Сравнивая значения коэффициентов  можно определить степень воздействия каждого фактора на результативный признак, при этом необходимо отметить, что коэффициенты чистой регрессии
можно определить степень воздействия каждого фактора на результативный признак, при этом необходимо отметить, что коэффициенты чистой регрессии  не сравнимы между собой.
не сравнимы между собой.
Например, если задано уравнение множественной регрессии в натуральном масштабе  , то из этого уравнения следует, что при изменении фактора
, то из этого уравнения следует, что при изменении фактора  на 1 единицу своего измерения результат
на 1 единицу своего измерения результат  изменится на 2,1 единицы своего измерения. При этом фактор
изменится на 2,1 единицы своего измерения. При этом фактор  считается неизменной величиной.
считается неизменной величиной.
Аналогично при изменении  на 1 единицу при неизменном уровне
на 1 единицу при неизменном уровне  фактор
фактор  меняется на 3,5 единиц.
меняется на 3,5 единиц.
Вышесказанное не означает, что фактор  сильнее влияет на результат
сильнее влияет на результат  .
.
Если получено уравнение множественной регрессии в стандартизованном масштабе для этой же задачи  , то в этом случае можно сказать, что с ростом
, то в этом случае можно сказать, что с ростом  на
на  при неизменном уровне
при неизменном уровне  результативный признак
результативный признак  изменится на
изменится на  , а с ростом
, а с ростом  на
на  при неизменном уровне
при неизменном уровне 
 увеличится на
увеличится на  . Следовательно, в данном случае на результативный признак
. Следовательно, в данном случае на результативный признак  более сильное воздействие оказывает фактор
более сильное воздействие оказывает фактор  .
.
Замечание
Для линейной парной зависимости стандартизованный коэффициент регрессии является линейным коэффициентом корреляции: 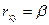 .
.
Между коэффициентами «чистой регрессии» и стандартизованным коэффициентом регрессии существует соотношение:  .
.
Последнее соотношение позволяет от уравнения множественной регрессии в стандартизованном масштабе переходить к уравнению множественной регрессии в натуральном масштабе, при чем свободный член  может быть найден из формулы:
может быть найден из формулы:  .
.
Если задано уравнение нелинейной множественной регрессии, то аналогично нелинейной парной регрессии данное уравнение либо с помощью замены переменного, либо с помощью процедуры логарифмирования преобразовывают к линейному виду множественной регрессии, т.е. линеаризуют. Затем параметры линеаризованной линейной модели определяют с помощью МНК; после определения параметра необходимо вернуться к первоначальной нелинейной модели множественной регрессии.
|
из
5.00
|
Обсуждение в статье: Тема 11. Оценка параметров уравнения множественной регрессии |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

