 |
Главная |
Средняя ошибка аппроксимации
|
из
5.00
|
Величина отклонения теоретического значения результативного признака  от фактического значения
от фактического значения  , взятая по модулю, представляет собой абсолютную ошибку аппроксимации:
, взятая по модулю, представляет собой абсолютную ошибку аппроксимации:  .
.
Величина, равная отношению абсолютной ошибки к фактическим значениям результативного признака, выраженная в процентах, называется относительной ошибкой аппроксимации: 
Чтобы иметь наиболее полное представление о качестве модели используют среднюю ошибку аппроксимации, которая равна средней арифметической относительных ошибок: 
Можно использовать также следующую формулу для определения средней ошибки аппроксимации: 
Полученное значение средней ошибки аппроксимации показывает, на сколько процентов в среднем теоретические значения результативного признака  отклоняются от фактических значений
отклоняются от фактических значений  .
.
Если полученное значение средней ошибки аппроксимации изменяется в пределах 5-7%, то это свидетельствует о хорошем подборе вида модели к исходным данным.
Если значение аппроксимации 8-10%, то это говорит о повышенной, но допустимой ошибке аппроксимации.
Нелинейная регрессия
Различают следующие классы нелинейных регрессий:
1) регрессии, нелинейные относительно включенных в анализ объясняющих переменных  , но линейные относительно оцениваемых параметров;
, но линейные относительно оцениваемых параметров;
2) регрессии, нелинейные по оцениваемым параметрам.
К первому классу регрессий можно отнести полиномы любых степеней 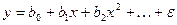 , равностороннюю гиперболу
, равностороннюю гиперболу  .
.
Ко второму классу регрессий относятся степенная регрессия  , показательная
, показательная  , экспоненциальная
, экспоненциальная  .
.
Нелинейные регрессии по включенным переменным позволяют оценить параметры регрессии с помощью МНК. Например, для оценки параметров полинома третьей степени  , достаточно воспользоваться заменой переменной
, достаточно воспользоваться заменой переменной  ,
,  , в результате чего получим линеаризованную модель:
, в результате чего получим линеаризованную модель:  , параметры которой оцениваются методом наименьших квадратов.
, параметры которой оцениваются методом наименьших квадратов.
Приведение нелинейной модели к линейному виду называется линеаризацией модели. В основном линеаризация осуществляется заменой переменного или с помощью логарифмирования уравнения регрессии (используют ln или lg).
Если задано уравнение параболы 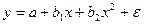 , то система нормальных уравнений для определения параметров
, то система нормальных уравнений для определения параметров  ,
,  ,
,  примет вид:
примет вид:
 решение которой возможно методом определителей:
решение которой возможно методом определителей:  ;
;  ;
;  ; где
; где  - определитель системы, а определители
- определитель системы, а определители 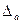 ,
,  ,
,  - частные определители , полученные заменой столбца свободных членов соответствующим столбцом коэффициентов. В виду симметричности параболы чаще всего используется не вся парабола, а какая-то ее часть.
- частные определители , полученные заменой столбца свободных членов соответствующим столбцом коэффициентов. В виду симметричности параболы чаще всего используется не вся парабола, а какая-то ее часть.
Для равносторонней гиперболы  , заменив
, заменив  , получают линейное уравнение
, получают линейное уравнение  , оценка параметров которого может быть дана МНК. Система нормальных уравнений примет вид:
, оценка параметров которого может быть дана МНК. Система нормальных уравнений примет вид: 
Регрессии, нелинейные по оцениваемым параметрам, делятся на два типа: нелинейные модели внутренне линейные и нелинейные модели внутренне нелинейные. Если нелинейная модель внутренне линейна, то она с помощью соответствующих преобразований может быть приведена к линейному виду. Если же нелинейная модель внутренне нелинейна, то она не может быть сведена к линейной функции.
Например, степенная модель  является нелинейной регрессией внутренне линейной, так как при логарифмировании обеих частей уравнения получаем линейную модель
является нелинейной регрессией внутренне линейной, так как при логарифмировании обеих частей уравнения получаем линейную модель  , параметры которой можно оценить МНК:
, параметры которой можно оценить МНК:  . Значение коэффициента регрессии b находят непосредственно из системы нормальных уравнений. Для нахождения значения параметра
. Значение коэффициента регрессии b находят непосредственно из системы нормальных уравнений. Для нахождения значения параметра  первоначально из системы находят значение
первоначально из системы находят значение  , а затем потенцированием определяют значение параметра:
, а затем потенцированием определяют значение параметра:  .
.
Однако, если степенную модель представить в виде  , то получится регрессия внутренне нелинейная.
, то получится регрессия внутренне нелинейная.
Обратная модель  линеаризуется с помощью замены
линеаризуется с помощью замены  , то есть получим линейную форму модели
, то есть получим линейную форму модели  .
.
Для преобразования нелинейной функции в линейную возможно и одновременное использование логарифмирования и замены.
Например, для функции  необходимо произвести замену
необходимо произвести замену  , а затем выполнить логарифмирование
, а затем выполнить логарифмирование  .
.
|
из
5.00
|
Обсуждение в статье: Средняя ошибка аппроксимации |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

