Спецификация модели множественной регрессии

Основной целью множественной регрессии является построение модели с большим числом факторов и определение при этом влияния каждого из факторов в отдельности на результат, а так же определение совокупного воздействия факторов на моделированный показатель.

Спецификация модели множественной регрессии включает в себя отбор фактора и выбор вида математической функции (выбор вида уравнения регрессии). Факторы, включаемые во множественную регрессию должны быть количественно измеримы и не должны быть интеркоррелированы и тем более находиться в точной функциональной связи (т.е. должны в меньшей степени влиять друг на друга, а в большей степени на результативный признак).

Включаемые во множественную регрессию факторы должны объяснять вариацию независимой переменной. Например, если строится модель с набором 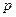- факторов, то для нее находится значение показателя детерминации , который фиксирует долю объясненной вариации результативного признака за счет 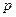- факторов.

Влияние других неучтенных факторов в модели оценивается как соответствующей остаточной дисперсии .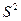

При включении в модель дополнительного 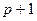фактора значение показателя детерминации должно возрастать, а значение остаточной дисперсии 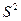должно уменьшиться. Если этого не происходит, то дополнительный фактор не улучшает модель и практически является лишним, причем введение такого фактора может привести к статистической не значимости параметров регрессии по - критерию Стьюдента.

Отбор факторов для множественной регрессии осуществляется в две стадии:

1. Подбираются факторы, исходя из сущности проблемы.

2. На основе матрицы показателей корреляции определяют статистики для параметров регрессии.

Коэффициенты корреляции между объясняющими переменными 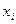, которые еще называют коэффициентами интеркорреляции, позволяют исключить из модели дублирующие факторы.

Две переменные 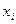и называют явно коллинеарными, если коэффициент корреляции .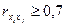

Если переменные явно коллинеарны, то они находятся в сильной линейной зависимости.

При наличии явно коллинеарных переменных предпочтение отдается не фактору более тесно связанному с результатом, а фактору, который при этом имеет наименьшую тесноту связи с другими факторами.

По величине парных коэффициентов корреляции обнаруживается лишь явная коллениарность факторов.

При использовании множественной регрессии может возникнуть мультиколлениарность фактов, т.е. более чем два фактора связаны между собой линейной зависимостью. В таких случаях менее надежным становится МНК при оценке отдельных факторов, результатом чего становится затруднение интерпретации параметров множественной регрессии как характеристик действия фактора в чистом виде. Параметры линейной регрессии теряют экономический смысл, оценки параметров ненадежны, возникают большие стандартные ошибки, которые при этом могут изменяться с изменением объема наблюдений, т.е. модель становится непригодной для анализа и прогнозирования экономической ситуации. Для оценки мультиколлениарности фактора используют следующие методы:

1. Определение матрицы парных коэффициентов корреляции между факторами, например, если задана линейная модель множественной регрессии , то определитель матрицы парных коэффициентов примет вид:

Если значение данного определителя равно 1

,

то факторы являются неколлинеарными между собой.

Если между факторами существует полная линейная зависимость, то все коэффициенты парной корреляции равны 1, в результате чего

.

2. Метод испытания гипотезы о независимости переменных. В этом случае нулевая гипотеза , доказано, что величина 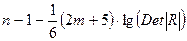имеет приближенное распределение с числом степеней свободы .

Если , то нулевая гипотеза отклоняется.

Определяя и сравнивая между собой коэффициенты множественной детерминации фактора, используя в качестве зависимой переменной последовательно каждой из факторов можно определить факторы, ответственные за мультиколлениарность, т.е. фактор с наибольшим значением величины .

Существуют следующие способы преодоления сильной межфакторной корреляции:

1) исключение из модели одного или несколько данных;

2) преобразование факторов для уменьшения корреляции;

3) совмещение уравнения регрессии, которые будут отражать не только факторы, но и их взаимодействие;

4) переход уравнения приведенной формы и др.

При построении уравнения множественной регрессии одним из важнейших этапов является отбор факторов, включаемых в модель. Различные подходы к отбору факторов на основе показателей корреляции к различным методам, среди которых наиболее применимы:

1) Метод исключения – производится отсев данных;

2) Метод включения – вводят дополнительный фактор;

3) Шаговый регрессионный анализ – исключают ранее введенный фактор.

При отборе факторов применяют следующее правило: число включаемых факторов обычно в 6-7 раз меньше объема совокупности, по которой строится модель.

Используются линейное и нелинейное уравнение множественной регрессии. Среди нелинейных моделей множественной регрессии наиболее часто применяется степенная модель. В общем виде нелинейное уравнение множественной регрессии: , либо . Коэффициенты , ,…, - называются коэффициентами «чистой регрессии».

Коэффициент «чистой регрессии» характеризует среднее значение результативного признака при изменении соответствующего фактора 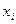на одну единицу своего измерения при неизменном уровне остальных факторов.

Параметр не подлежит экономической интерпретации. В степенной модели нелинейное уравнение множественной регрессии коэффициенты , ,…, являются коэффициентами эластичности, которые показывают насколько, в среднем, изменится результат при изменении соответствующего фактора на 1% при неизменном воздействии остальных факторов.