 |
Главная |
Типы показательно-степенных уравнений и способы их решения
|
из
5.00
|
Всюду далее f(x), g(x), h(x) – некоторые выражения с неизвестной x.
I тип:
 .(6)
.(6)
Решение уравнения (6) на ОДЗ сводится к решению совокупности
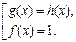
II тип:
 .(7)
.(7)
Решение уравнения (7) на ОДЗ сводится к решению совокупности

Пример 1. Решить уравнение  .
.
Решение. Способ 1. Имеем уравнение типа (2). Решаем логарифмированием по основанию 3. Получаем
 , т.е.
, т.е. 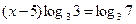 . Приходим к линейному уравнению
. Приходим к линейному уравнению  , откуда
, откуда  .
.
Способ 2. Преобразуем правую часть при помощи основного логарифмического тождества:  .
.
Получили уравнение типа (4), которое решаем по свойству равенства степеней:
 .
.
Пришли к ответу:  .
.
Пример 2. Решить уравнение  .
.
Решение. Выполним необходимые преобразования; сведем показательные выражения к одному и тому же основанию 3.

По свойству степеней  ,
,  .
.
Получаем ответ: 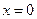 .
.
Пример 3. Решить уравнение 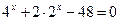 .
.
Решение. Преобразуем уравнение

Имеем квадратное уравнение относительно  . Решаем при помощи замены
. Решаем при помощи замены  . Получаем
. Получаем
 .
.
Корнями последнего уравнения являются значения 
 .
.
Возвращаясь к неизвестной x, имеем совокупность:
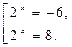
Первое уравнение совокупности решений не имеет. Решаем второе уравнение:
 , т.е.
, т.е.  .
.
Получили ответ:  .
.
Пример 4. Решить уравнение  .
.
Решение. Выполним необходимые преобразования

Имеем однородное уравнение. Разделим обе части уравнения на 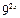
 . Получим:
. Получим:
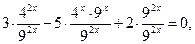
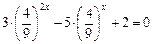 ,
,
т.е. получили квадратное уравнение относительно  . Вводим замену
. Вводим замену  . Тогда
. Тогда

откуда
 .
.
Возвращаемся к старой переменной:

Получили ответ: 
Пример 5. Решить уравнение 
Решение. 1 способ. Подбором убеждаемся, что  – корень уравнения. Функции
– корень уравнения. Функции  (т.е.
(т.е.  ) и
) и  монотонно возрастают (рис.12). Они имеют единственную общую точку.
монотонно возрастают (рис.12). Они имеют единственную общую точку.

Рис. 12
Способ 2.Разделим обе части уравнения на  . Получим
. Получим
 или
или  .
.
Заменим  . Получим
. Получим  .
.
При  получим основное тригонометрическое тождество. Т.е.
получим основное тригонометрическое тождество. Т.е.  является корнем исходного уравнения.
является корнем исходного уравнения.
Получили ответ:  .
.
Пример 6. Решить уравнение  .
.
Решение. ОДЗ: x = 2, 3, …, n, … .
Перепишем уравнение в виде
 .
.
Разделим обе части уравнения на  (т.к.
(т.к. 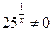 ). Получим:
). Получим:
 .
.
Вводим замену 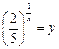 . Получаем квадратное уравнение
. Получаем квадратное уравнение  , откуда
, откуда 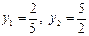 .
.
Возвращаемся к старой переменной:

Но ни один из корней не подходит по ОДЗ. Следовательно, уравнение корней не имеет.
Пример 7. Решить уравнение 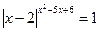 .
.
Решение.ОДЗ: x ¹ 2.
 .
.
Решением является совокупность

Корень x = 2 не подходит по ОДЗ.
Получили ответ: x = 1, x = 3.
Задания
I уровень
1.1. Установить, имеет ли уравнение корни:
1) 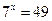 ; 2)
; 2)  ;
;
3) 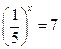 ; 4)
; 4)  ;
;
5) 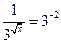 ; 6)
; 6)  ;
;
7)  .
.
1.2. Определите, сколько корней имеет уравнение 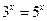 . Как это можно установить графически ?
. Как это можно установить графически ?
1.3. Решите уравнения:
1)  ; 2)
; 2)  ;
;
3)  ; 4)
; 4)  ;
;
5)  ; 6)
; 6) 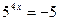 ;
;
7)  ; 8)
; 8)  ;
;
9)  ; 10)
; 10)  ;
;
11)  ; 12)
; 12)  ;
;
13)  .
.
II уровень
2.1. Решите уравнение:
1)  ;
;
2)  ;
;
3)  ;
;
4)  ;
;
5)  ;
;
6)  ;
;
7) 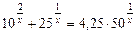 ;
;
8)  ;
;
9) 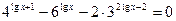 ;
;
10)  ;
;
11)  ;
;
12) 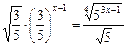 ;
;
13)  ;
;
14)  ;
;
2.2. Найдите значение выражения  , если
, если  .
.
III уровень
3.1. Решите уравнение:
1)  ;
;
2)  ;
;
3) 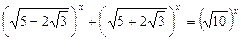 ;
;
4)  ;
;
5)  ;
;
6)  ;
;
7) 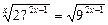 ;
;
8) 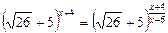 ;
;
9)  ;
;
10)  ;
;
11) 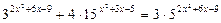 ;
;
12)  ;
;
13) 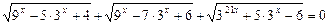 ;
;
14) 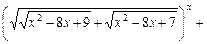
 ;
;
15)  ;
;
16)  ;
;
17)  ;
;
3.2. Найдите сумму корней уравнения
 .
.
|
из
5.00
|
Обсуждение в статье: Типы показательно-степенных уравнений и способы их решения |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

