 |
Главная |
Числовые характеристики случайных величин
|
из
5.00
|
Случайная величина может быть описана частично с помощью числовых характеристик.
Числовые характеристики –наиболее существенные особенности распределения.
Различают:
1) Характеристики положения: математическое ожидание, мода, медиана.
Математическим ожиданием (МО)  или
или 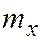 случайной величины
случайной величины  называется ее среднее значение.
называется ее среднее значение.  имеет размерность СВ.
имеет размерность СВ.
МО обладает свойствами:
1. МО постоянной величины  равно самой постоянной:
равно самой постоянной: 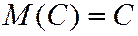 .
.
2. Постоянный множитель можно выносить за знак МО:  .
.
3. МО произведения двух независимых случайных величин равна произведению их МО  .
.
МО произведения нескольких взаимно независимых случайных величин равно произведению их математических ожиданий. Например, для трех СВ 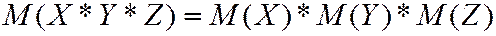 .
.
Произведение двух независимыхслучайных величин  и
и  - это случайная величина
- это случайная величина  , возможные значения которой равны произведениям возможных значений СВ
, возможные значения которой равны произведениям возможных значений СВ  на возможные значения СВ
на возможные значения СВ  .
.
Две случайные величины называются независимыми, если закон распределения одной из них не зависим от того, какие возможные значения приняла другая величина. В противном случае случайные величины зависимые.
Несколько СВ взаимно независимы, если законы распределения любого числа из них не зависят от того, какие значения приняли остальные величины.
4. МО суммы двух случайных величин равно сумме математических ожиданий слагаемых  .
.
МО суммы нескольких случайных величин равно сумме математических ожиданий слагаемых. Например, для трех СВ 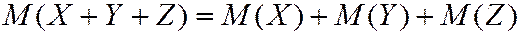 .
.
Суммой случайных величин  и
и  называют СВ
называют СВ 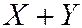 , возможные значения которой равны суммам возможных значений СВ
, возможные значения которой равны суммам возможных значений СВ  с возможными значениями СВ
с возможными значениями СВ  .
.
Модой  случайной величины
случайной величины  называется ее наиболее вероятное значение
называется ее наиболее вероятное значение
Медианой  случайной величины
случайной величины  называется такое ее значение, для которого
называется такое ее значение, для которого  , т.е. одинаково вероятно, окажется ли случайная величина меньше или больше
, т.е. одинаково вероятно, окажется ли случайная величина меньше или больше  .
.
2) Характеристики рассеяния (разбросанность значений случайной величины около ее математического ожидания): дисперсия, среднее квадратическое отклонение.
Дисперсия 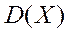 или
или  случайной величины
случайной величины  - это математическое ожидание квадрата разности между случайной величиной
- это математическое ожидание квадрата разности между случайной величиной  и ее математическим ожиданием.
и ее математическим ожиданием.
Разность между СВ  и ее МО называется отклонением или центрированной СВ.
и ее МО называется отклонением или центрированной СВ.
МО отклонения равно 0.  .
.
Размерность  равна квадрату СВ.
равна квадрату СВ.
Свойства дисперсии:
1. Дисперсия постоянной величины С равна 0:  .
.
2. Постоянный множитель можно выносить за знак дисперсии, возводим его в квадрат 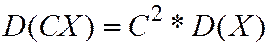
3. Дисперсия суммы двух независимых случайных величин равна сумме дисперсии этих величин

Дисперсия суммы нескольких взаимно независимых случайных величин равна сумме дисперсии этих величин. Например, для трех СВ

Дисперсия суммы постоянной величины и СВ равна дисперсии СВ

4. Дисперсия разности двух независимых случайных величин равна сумме их дисперсии

Среднее квадратическое отклонение 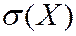 или
или случайной величины
случайной величины  - это положительное значение корня квадратного из дисперсии. Предназначена для более наглядного представления характеристики «рассеяния», т.к. имеет размерность случайной величины в отличие от дисперсии. Может быть также использована для ориентировочной оценки диапазона возможных значений СВ. Диапазон практически возможных значений СВ
- это положительное значение корня квадратного из дисперсии. Предназначена для более наглядного представления характеристики «рассеяния», т.к. имеет размерность случайной величины в отличие от дисперсии. Может быть также использована для ориентировочной оценки диапазона возможных значений СВ. Диапазон практически возможных значений СВ  не выходит за пределы
не выходит за пределы
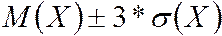 ,
,
т.н. правило трех сигм.
3) Начальный теоретический момент  -го порядка
-го порядка 
 или
или  случайной величины
случайной величины  - математическое ожидание
- математическое ожидание  -ой степени этой случайной величины. Начальный момент нулевого порядка равен
-ой степени этой случайной величины. Начальный момент нулевого порядка равен  . Начальный момент первого порядка (первый момент) есть, МО
. Начальный момент первого порядка (первый момент) есть, МО 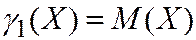
4) Центральный теоретический момент  -го порядка
-го порядка 
 или
или  случайной величины
случайной величины  - математическое ожидание
- математическое ожидание  -ой степени отклонения (разности между случайной величиной
-ой степени отклонения (разности между случайной величиной  и ее математическим ожиданием).
и ее математическим ожиданием).
Центральный момент 0-го порядка равен 1.


Центральный момент 1-го порядка равен 0.

Центральный момент 2-го порядка есть дисперсия.

Центральный момент 3-го порядка служит для характеристики ассиметрии относительно МО (или «скошенности» распределения) и используется в формуле для расчета коэффициента ассиметрии (или просто ассиметрии).

Центральный момент 4-го порядка служит для характеристики так называемой «крутости», т.е. «островершинности» или «плосковершинности» распределения, который называется эксцесс

Центральные моменты выражаются через начальные

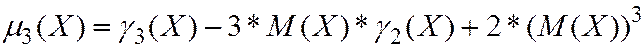
|
из
5.00
|
Обсуждение в статье: Числовые характеристики случайных величин |
|
Обсуждений еще не было, будьте первым... ↓↓↓ |

Почему 1285321 студент выбрали МегаОбучалку...
Система поиска информации
Мобильная версия сайта
Удобная навигация
Нет шокирующей рекламы

