Основные (типовые) распределения ДСВ

СВ называется распределенной по биномиальному закону, если её возможные значения , а соответствующие вероятности рассчитываются по формуле Бернулли (2.22)

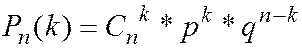
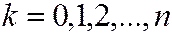
- число появления события в 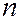независимых испытаниях.

Биномиальное распределение зависит от двух параметров 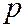и .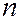

Ряд распределения имеет вид:

				…

 

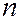
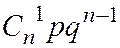
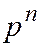
(3.7)

 

Пример.Проверить формулы (3.7) для примера рассмотренного выше.

Решение.

, ,

ДСВ называется распределенной по закону Пуассона,если её возможные значения , а соответствующие вероятности выражаются формулой Пуассона (2.24)

Распределение Пуассона зависит от одного параметра - среднее число появления событий при 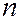испытаниях.

Ряд распределения имеет вид:

				…

 

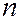
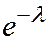
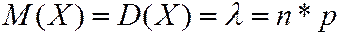(3.8)

Пуассоновское распределение является предельным для биномиального при , , 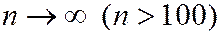если .

Пример:

1. Устройство имеет 1000 элементов, которые работают независимо один от другого. Вероятность того, что элемент выйдет из строя во время работы . Определить среднее количество элементов, которые могут выйти из строя.

Решение.

2. На АТС на протяжении часа поступает в среднем 30 вызовов. Найти вероятность того, что на протяжении минуты поступит не более 2-х вызовов.

Решение.

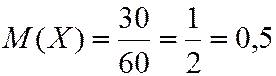- среднее число

вызовов за одну минуту

ДСВ называется распределенной по гипергеометрическому закону,если её возможные значения , а соответствующие вероятности определяются гипергеометрической формулой (1.7).

,

 

Гипергеометрическое распределение зависит от трех параметров .

Ряд распределения имеет вид:

				…

 

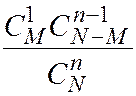
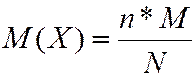
(3.9)

При гипергеометрическое распределение дает вероятности, близкие к вероятностям, найденным по биномиальному закону.

Пример.В ящике имеется 10 однотипных деталей, из них 7 стандартных. Из ящика берут 4 детали. Построить ряд распределения ДСВ – числа стандартных деталей среди отобранных.

Решение.

 

;

;

;

;

ДСВ называется распределенной по равномерному закону, если ее возможные значения , а соответствующие им вероятности можно рассчитать по формуле

, .

Равномерное распределение зависит от одного параметра .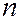

Ряд распределения имеет вид:

			…
			…

,

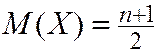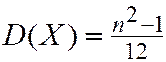
Пример.На связке 5 ключей, из которых только один подходит к замку. Составить ряд распределения ДСВ числа ключей, которые пробуются для открытия замка.

 

 

 

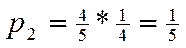
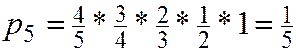
ДСВ имеет геометрическое распределение, если ее возможные значения а вероятности этих значений .

Вероятности для ряда последовательных значений образуют бесконечно убывающую геометрическую прогрессию со знаменателем .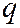

Ряд распределения имеет вид:

				…		…
				…		…

 

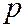
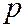
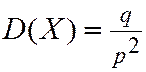, (3.10)

Нередко рассматривают СВ , равную числу попыток до получения результата, включая удавшуюся попытку, т.н. геометрическое распределение начинающееся с «1», для которого

Ряд распределения СВ :

			…		…
			…		…

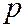
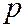
, (3.11)

Геометрическое распределение зависит от одного параметра .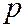

Пример. Из корзины, в котором 3 черных и два белых шара последовательно вынимают шары до появления белого. Перед очередным извлечением шара, вынутый ранее шар возвращается в корзину. Построить ряд распределения ДСВ - числа вынутых белых шаров до появления черного и ДСВ - количество попыток до появления черного шара.

Решение:

 

				…
				…

 

				…
				…

 

 

Непрерывные СВ

Непрерывной СВ в широком смысле называется СВ, которая может принимать все (бесконечно много) значения из некоторого конечного или бесконечного промежутка. Если функция распределения 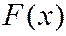везде непрерывна и имеет производную, СВ называется непрерывной в узком смысле.

Пример:

1. Координаты точки попадания при выстреле.

2. Время опоздания поезда.

3. Время безотказной работы лампы.

 

 

3.5.1. Формы представления закона распределения НСВ

 

Ряд распределения, многоугольник распределения и формула не используются в качестве закона распределения НСВ.

Функция распределения НСВ , есть непрерывная, кусочно-дифференцируема функция с непрерывной производной.

 

График функции распределения НСВ , которая принимает все возможные значения на интервале .

Из свойства 2 функции распределения вытекает важное следствие для НСВ: вероятность того, что НСВ примет одно определенное значение равна 0. И тогда

Таким образом, не представляет интереса говорить о вероятности того, что НСВ примет одно определенное значение, но имеет смысл рассматривать вероятность попадания ее в интервал, пусть даже сколь угодно малой.

При этом надо понимать, что не означает, что событие невозможно. В результате испытания НСВ обязательно примет одно из возможных значений, в том числе и .

Плотность вероятностей (плотность распределения вероятностей, плотность) НСВ - функция, определяемая как первая производная функции распределения

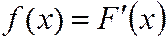(3.12)

Из определения следует, что - есть первообразная и выражается через формулой.

(3.13)

Геометрически есть площадь кривой распределения, лежащая левее точки .

График называется кривой распределения.

Размерность обратна размерности СВ (это не вероятность).

Свойства :

1. неотрицательная функция, т.е.

2.Несобственный интеграл от на интервале 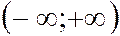равен 1.

(3.14)

Это так называемое условие нормировки плотности распределения.

Если все возможные значения НСВ принадлежат интервалу , то

(3.15)

3. Вероятность того, что НСВ примет значение из интервала равна определенному интегралу от , взятому на интервале

(3.16)

Геометрически это означает, что есть площадь под кривой распределения, ограниченная линиями и слева и справа соответственно и осью абсцисс внизу.

Величина для НСВ называется элементом вероятностии приближенно равна вероятности попадания СВ на элементарный отрезок , примыкающий к точке .

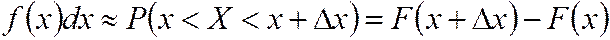(3.17)

Пример.Для НСВ , плотность распределения которой имеет вид

1) Определить коэффициент ;

2) Построить кривую распределения;

3) Найти и построить её график;

4) Вычислить

Решение:

1. По (3.14)

2. Кривая распределения

 

3. По (3.13)

При

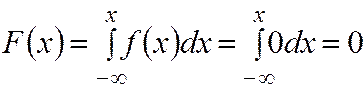
При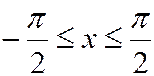

 

При

 

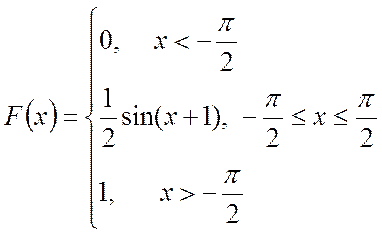
График функции

 

 

4. Согласно второго свойства