Алгоритмизация методов расчета режимов

Алгоритм расчета режима электрической сети не ограничивается только решением уравнений режима. В целом расчет режима включает следующие этапы:

1. Определение параметров схемы замещения электрической сети.

2. Вычисление параметров (коэффициентов) уравнений режима.

3. Решение уравнений режима (вычисление напряжений в узлах сети).

4. Расчет токов, мощностей и потерь мощности.

Примерная блок-схема алгоритма расчета режима электрической сети на ЭВМ показана на рис. 2.4.

На этапе определения параметров схемы замещения вычисляются:

– сопротивления продольных ветвей R_ij, X_ij (i, j – номера узлов в начале и конце ветви);

– проводимости поперечных ветвей G_i, B_i (i – номер узла, от которого отходит данная поперечная ветвь);

– коэффициенты трансформации идеальных трансформаторов k_трi,j (трансформация производится от узла i к узлу j).

Для примера на рис. 2.2 показан фрагмент сети, содержащий воздушную линию ВЛ, двухобмоточный трансформатор Т, кабельную линию КЛ и нагрузку S. Схема замещения приведена на рис. 2.3. На этой схеме Z_1,2 = R_1,2 + jX_1,2 – сопротивление воздушной линии; Z_2,3 = R_2,3 + jX_2,3 – сопротивление трансформатора; R_3,4 – сопротивление кабельной линии (активное). Проводимости поперечных ветвей имеются только в узлах 1 и 2: B₁ = –B_л, G₂ = G_т, B₂ = B_т – B_л. Здесь B_л – емкостная проводимость воздушной линии; G_т и B_т – активная и индуктивная проводимости ветви намагничивания трансформатора, которые соответствуют комплексной проводимости Y_т.

Вычисление параметров уравнений режима включает:

– расчет взаимных проводимостей узлов сети g_ij, b_ij;

Вычисление параметров уравнений режима включает:

– расчет взаимных проводимостей узлов сети g_ii, b_ii;

– приведение сети к одному уровню напряжения;

– расчет собственных проводимостей узлов сети g_ii, b_ii;

– при необходимости – вычисление некоторых других параметров.

Взаимная проводимость в комплексной форме

.

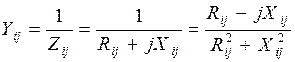Отсюда получаем следующие расчетные выражения для активной и индуктивной проводимостей:

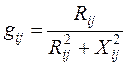, . (2.49)

После расчета взаимных проводимостей сеть приводится к одному классу напряжения. Приведение осуществляется по фактическим коэффициентам трансформации. Обычно сеть приводится к наиболее высокому уровню напряжения.

Операция приведения сети к одному классу напряжения заключается в пересчете взаимных проводимостей и проводимостей поперечных ветвей. Приведенная проводимость получается путем деления исходной проводимости на произведение квадратов коэффициентов трансформации, отделяющих участок сети, к которому осуществляется приведение, от участка сети, которому принадлежит данная проводимость:

, . (2.50)

Например, если сеть, показанная на рис. 2.3, приводится к уровню напряжения воздушной линии, то проводимость кабеля пересчитывается по формуле

.

Следующим шагом при определении параметров уравнений является расчет собственных проводимостей узлов. Эти проводимости вычисляются путем суммирования взаимных проводимостей ветвей, сходящихся в данном узле, и проводимости поперечной ветви данного узла. Например, собственные проводимости узла 2 на рис. 2.3 равны

, .

После определения всех параметров уравнений режима осуществляется решение этих уравнений. Данный шаг представляет собой «ядро» алгоритма расчета режима электрической сети, к которому относится основное количество вычислительных операций. В результате определяются напряжения в узлах сети, приведенные к одному классу напряжения.

На заключительном этапе расчета режима осуществляется:

– вычисление мощностей, передаваемых через элементы сети;

– расчет генерируемых мощностей и мощностей потребителей (за исключением тех, которые являются постоянными);

– определение потерь мощности в элементах сети и суммарных потерь мощности;

– вычисление токов в ветвях сети;

– обратное приведение параметров режима к фактическим классам напряжения.

Расчет токов, мощностей и потерь мощности производится через напряжения по достаточно простым формулам, которые в комплексной форме приведены в п. 1.2. Параллельно осуществляется обратное приведение параметров режима к фактическим классам напряжения. При этом токи могут быть вычислены как до обратного приведения напряжений, так и после. В первом случае обратное приведение производится для токов и напряжений, а во втором случае – только для напряжений.

2.6. Учет слабой заполненности матрицы
узловых проводимостей

Одним из топологических свойств электрических сетей является слабая заполненность (разреженность) матрицы узловых проводимостей. Каждый узел сети соединяется лишь с небольшим числом других узлов, и, таким образом, значительная часть взаимных проводимостей равна нулю. При этом чем больше узлов содержит сеть, тем менее заполненной является матрица узловых проводимостей.

Правильный учет данного свойства при расчетах режимов позволяет существенно уменьшить объем вычислений и используемой памяти ЭВМ. Существуют различные способы учета разреженности матрицы узловых проводимостей.

Достаточно простым и в то же время эффективным способом является приведение матрицы к ленточному типу путем изменения нумерации узлов. Оно осуществляется по следующим правилам:

1. Выбирается узел с наименьшей степенью (степенью называется число ветвей, сходящихся в данном узле) или один из таких узлов, если их несколько. Этому узлу присваивается номер 1.

2. Нумеруются узлы, смежные с узлом 1, в порядке возрастания их степеней.

3. То же самое производится для остальных пронумерованных узлов в порядке возрастания их номеров.

В качестве примера на рис. 2.5 приведена схема сети, узлы которой пронумерованы по данным правилам.

Построена также матрица соединений узлов сети S. Если узлы, соответствующие номерам строки и столбца, соединены друг с другом, то данный элемент матрицы равен 1. В противном случае соответствующий элемент равен 0. Элементы главной диагонали равны 1.

Матрица соединений имеет то же расположение нулевых элементов, что и матрица узловых проводимостей. Видно, что полученная ниже матрица относится к ленточному типу.

2.7. Существование, единственность и устойчивость
решения уравнений режима

Данный вопрос в целом рассмотрен в [1]. Ниже приводятся только основные положения.

Уравнения режима электрической сети обычно имеют не одно решение, а несколько (на практике – два). Наличие нескольких решений обусловлено нелинейностью уравнений. При этом одно из двух решений является устойчивым, а другое – неустойчивым.

Повышение нагрузок потребителей и/или понижение напряжений источников приводит к тому, что устойчивое и неустойчивое решения «сближаются». Режим, при котором эти решения совпадают, называется предельным по статической устойчивости.

При еще более низких напряжениях источников или более высоких нагрузках установившегося режима не существует.

Чем больше сопротивления элементов сети, тем ближе предел по статической устойчивости и вероятнее «исчезновение» режима.