Канонические уравнения метода сил и их упрощение

Теоремы об упругих системах, рассмотренные выше (ранее), являются основой для современных методов расчета статически неопределимых систем. Различают два метода расчета статически неопределимых систем: метод сил и метод перемещений. В расчете статически неопределимых систем по методу сил в качестве неизвестных принимаются внутренние усилия в лишних связях.

Расчет по методу сил статически неопределимых систем в ТТ является наиболее распространенным, поэтому методу расчет начинают с выбора основной системы. Основной называют такую статически определимую и геометрически неизменяемую систему, которая после удаления лишних связей в заданной системе и замены их неизвестными усилиями находится в таком же напряженно-деформированном состоянии, что и заданная система. Следует иметь в виду, что для одной и той же заданной системы может быть несколько вариантов основной системы.

Поэтому нужно стремиться к наиболее рациональной основной системе, в наибольшей степени, упрощающей расчет.

После выбора основной системы расчет осуществляется в следующей последовательности. К основной системе кроме заданной нагрузки по направлению отвращенных связей прикладываются неизвестные силы, называемые лишними неизвестными: Х_1, Х_2, Х₃ и т.д.

Неизвестные силы подбираются с таким расчетом, чтобы перемещения в основной и заданной системах были равны. Перемещения по направлению какой-либо неизвестной силы будут равняться нулю, независимо от того, где она приложена – на опоре или в рассеченном элементе, поскольку в заданной системе перемещения по направлению неизвестных сил отсутствуют. Следующим типом расчета будет составление уравнений совместности перемещений, которые выражают условие равенства нулю перемещений по направлению каждой лишней связей.

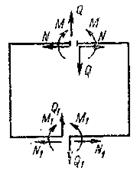
Рисунок 43 – Схема портальных рам

Рассмотрим, например, приведенную на рис.44, а неразрезную балку с числом лишних связей, равным n. Основную систему выберем путем удаления лишних опорных стержней и замены их неизвестными силами (рис.44, б). Столь неудачный в данном случае выбор основной системы сделан специально для того, чтобы сохранить в системе канонических уравнений все их члены.

В этом случае система n уравнений может быть записана так:

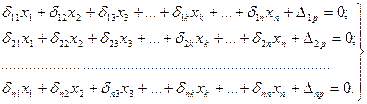(85)

Уравнения совместности перемещений называются каноническими уравнениями метода сил, поскольку они записываются по определенному закону. Эти уравнения, количество которых равна числу лишних неизвестных, совместно с уравнениями равновесия позволяют раскрыть статическую неопределимость системы, т.е. определить значения лишних неизвестных. Неизвестными в них являются реакции отброшенных связей Х_1, Х_2, Х₃ и т.д.

В качестве коэффициентов при неизвестных стоят перемещения основной системы, вызванные единичными силами, действующими по направлению неизвестных (рис.44, в-е), и внешней нагрузкой (рис.44, ж).

Левые части уравнений (85) выражают суммарные перемещения точек приложения неизвестных сил по их направлениям от действия приложенных сил. Поскольку в заданной системе эти перемещения отсутствуют, приравниваем их нулю. Для выяснения смысла уравнений (85) рассмотрим содержание одного из них, например второго. Множитель δ₂₁ в первом члене представляет собой перемещение точки приложения силы Х₂ по её направлению вызванное единичной силой Х₁; произведение δ₂₁х₁ – перемещение точки 2, вызванное силой х₁. Следующий член δ₂₂х₂₂ выражает перемещение точки приложения силы х₂ по её направлению, вызванное той же силой х₂ и т.д. Свободный член представляет собой перемещение точки приложения силы х₂ по её направлению, вызванное заданной внешней нагрузкой. Буква для свободного члена ставится в отличие от δ, потому что это перемещение не от единичной силы, а от всей заданной внешней нагрузки, т.е. . Во многих случаях рациональный выбор основной системы может существенно упростить вычисления системы уравнений (85). Канонические уравнения представляют собой систему линейных уравнений, решение которых не представляет принципиальных трудностей, одного при большем числе уравнений трудоемко. В первую очередь надо вычислить большое число перемещений. Коэффициенты при неизвестных образуют квадратную симметричную матрицу (85)

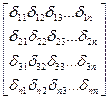(86)

В представленной матрице коэффициенты δ_ii называются главными перемещениями, а δ_ij (i 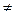j) побочными. Главные перемещения, расположенные по диагонали матрицы, всегда положительны, что следует из формулы Мора (80), и не могут обратиться в нуль. Побочные перемещения, расположенные симметрично по отношению к диагонали матрицы, вследствие закона взаимности перемещений соответственно равны между собой. Побочные перемещения могут быть положительными, отрицательными или обращаться в нуль. Это свойство побочных перемещений дают возможность упрощать систему уравнений (85). Необходимо выбирать основную систему так, чтобы возможно большее число побочных перемещений обратилось в нуль. Наиболее простым будет решение, если все побочные перемещения обратятся в нуль. В этом случае все неизвестные будут разделены, т.е.

δ₁₁x₁+ _1p= 0, δ₂₂x₂ + _2p= 0, …, δ_mnx_n + _np = 0 (87)

Конечно, такое упрощенное решение удается получить не всегда.

Для решения системы уравнений (85)существует ряд способов, в том числе в матричной форме с применением цифровых ЭВМ.

Побочные перемещения по правилу Верещагина, когда одна из эпюр моментов прямолинейна, определяются по следующим формулам: или , где y_k и y_n ординаты прямолинейной эпюры, расположенные под центром тяжести второй рассматриваемой эпюры, значение может равняться нулю при одном из следующих ниже приведенных условий.

1. Из двух рассматриваемых эпюр моментов, соответствующих состояниям n и k, одна эпюра симметрична, а другая – кососимметрична. Тогда при определенной δ_nk половина суммы будет иметь один знак, а вторая половина – противоположный.

2. На каждом из участков двух рассматриваемых эпюр моментов, соответствующих состояниям n (рис.45, а) и k (рис.45, в), в одной из эпюр моменты по всей длине участка равны нулю.

3. На протяжении каждого участка одна из эпюр прямолинейна и имеет нулевую ординату против центра тяжести другой эпюры соответствующего участка.

Поясним первое и третье правила на примере. На рис.46,а показана заданная система (нагрузка не показана, так как в данном случае это не имеет значения) и неудачный вариант основной системы (рис.46, б). Из единичных эпюр изгибающих моментов М₁ – М₃ (рис.46, е-д) видно, что ни одно из побочных перемещений не обращается в нуль. На рисунке 47 для той же заданной системы показана такая основная система (рис.47, а) при которой эпюры изгибающих моментов М₁ (рис.47, б) и М₂ (рис.47, в) симметричны, а М₃ косо симметрична (рис.47, г). Тогда в соответствии с первым условием δ₁₃=0 и δ₂₃=0. Система уравнений распалась на две – два совместных уравнения с двумя неизвестными и одно уравнение с одним неизвестным:

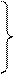
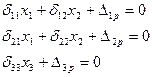(88)

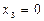Если рама нагружена симметричной нагрузкой, дающей симметричную эпюру, то , т.е. и система лишь дважды статически неопределима. Если рама нагружена только кососимметричной нагрузкой, то , т.е. и система лишь раз статически неопределима.

Литература: Основная: 3[разд.2:с.32-34; 39-48]; 6[разд.2:с.47-57]

Контрольные вопросы:

1 Чему равна работа внутренних сил и как определяется потенциальная энергия плоской системы, напишите выражения полной потенциальной энергии для плоской и пространственной стержневой систем, состоящих из прямолинейных стержней, а также дайте интерпретацию составляющим членам?

2 В чем заключается смысл теоремы о взаимности реакций, как она называется и читается?

3 Приведите доказательство теоремы о взаимности реакций и в чем заключается смысл теоремы о взаимности реакций и перемещений как она называется?

4 На чем основывается вывод формулы перемещений, и напишите формулу Мора для плоской и пространственной стержневой систем и дайте им анализ?

5 Что является основой для современных методов расчета статически неопределимых систем, сколько и какие методы применяют, а также как производится расчет в ТТ по методу сил и какой последовательности?

6 Какие уравнения называются каноническими уравнениями метода сил и что они позволяют достигнуть, систему, каких зависимостей представляют собой канонические уравнения и как производится их решение и в чем заключается смысл побочных перемещений по правилу Верещагина?

Рисунок 44 – Неразрезная балка Рисунок 46 – Пример неудачного варианта

основной системы.

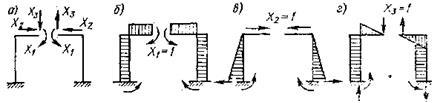
Рисунок 47 – Пример варианта основной системы с симметричными и косо симметричными эпюрами

7.Тема лекции: Расчет статически неопределимых балок и ферм.

Неразрезной называется статически неопределимая балка, которая имеет не менее двух пролетов и не имеет шарниров или разрезов. Статически неопределимой неразрезная двухпролетная балка может быть только в том случае, когда она закреплена тремя опорными стержнями, не пересекающимися в одной точке и параллельными между собой (рис.48).

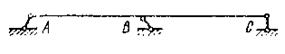
А, В, С – опорные стержни

Рисунок 48 – Статически определимая

двухпролетная балка

Рисунок 49 – Неразрезные балки