Уравнение трех моментов

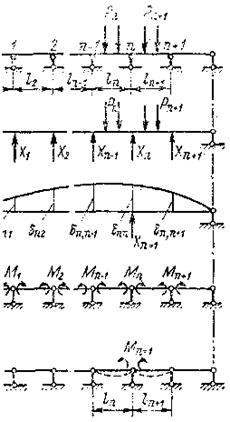
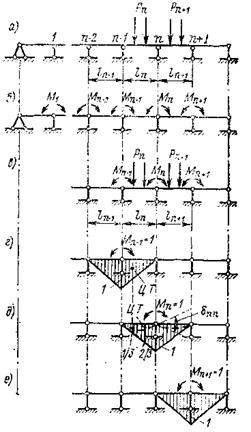
На рис.51, а показана неразрезная многоопорная балка. В основной системе жесткую связь на каждой опоре заменим на шарнирную. В результате получим совокупность однопролетных шарнирно опертых балок (рис.51, б). За неизвестные примем изгибающие моменты, действующие в опорных сечениях, и обозначим их М_{1 ,…,} М_n-1, М_n, М_n+1. Предположим, что все моменты имеют одно направление – растягивают нижние волокна балки. Если для какого-то момента получим отрицательное значение, то это будет означать, что момент направлен в другую систему. Для определения взаимного поворота сечений (перелома упругой линии на опоре n) возьмем смежные опоры n-1, n и n+1 (рис.51, г-е). Приложим в опорах единичные изгибающие моменты М_n-1, М_n и М_n+1 Из построенных эпюр видно, что каждая из эпюр, например эпюра М_n, перекрывается только частями эпюр М_n-1 и М_n+1, а эпюрами остальных единичных состояний не перекрывается. Поэтому в каждом каноническом уравнении будет не более трех неизвестных (в первом и последнем – по два) и каноническое уравнение для перелома сечений на опоре n, которого в действительности нет, будет равно нулю и иметь следующий вид:

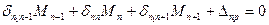(90)

Для нахождения m_n-1, m_n и m_n+1 надо определить коэффициенты при неизвестных. Пренебрегая влиянием поперечных сил на деформацию балки, получим 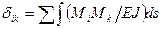. Поскольку моменты инерции в разных пролетах могут быть разными, то для упрощения расчетов более целесообразно вычислять не 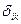, а произведени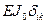е , где 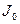– произвольный момент инерции.

Коэффициенты при неизвестных определяются путем перемножения единичных эпюр:

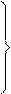
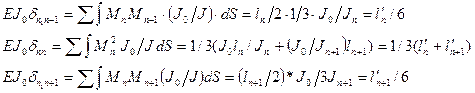(91)

Величины 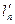и 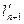называются приведенными пролетами и равны:

;

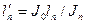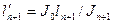
Определим теперь поворот сечения на опоре n от заданной нагрузки, приложенной в пролетах 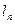и l_n+1, так как он зависит от загружения только этих пролетов (рис.52, а):

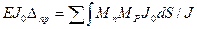. (92)

Так как эпюра единичного состояния М_п (рис.52, в) состоит из двух прямых участков, то перемещение 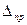определяется по правилу Верещагина как произведение площади криволинейной эпюры М_р на ординату из прямоугольной эпюры. Находящуюся под центром тяжести (ЦТ) эпюры М_р. Отсюда

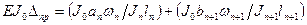(93)

где ω_n и 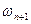– площади эпюр; а_п, b_n и a_n+1, b_n+1 расстояния от центров тяжести (ЦТ) эпюр до опор. Произведение 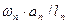представляет собой правую опорную реакцию 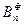пролета l_п от фиктивной нагрузки ω_п. Аналогично произведение 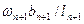представляет собой левую опорную реакцию 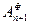пролета 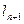от фиктивной нагрузки ω_п+1. Тогда 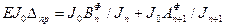(94)

Поставляя полученные значения в уравнение (90), получим

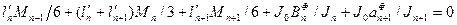(95)

В этом случае, когда момент инерции постоянен во всех пролетах, т.е. J₀=J, уравнение имеет вид

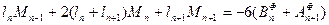(96)

Это уравнение называется уравнением трех моментов, так как оно связывает три неизвестных опорных момента. Для расчета неразрезной балки нужно составить столько уравнений, сколько лишних неизвестных она имеет. В случае, когда конец балки заделан, при расчете вводится фиктивный пролет длиной l₀, стремящийся к нулю, с шарнирной опорой. Зная опорные моменты, легко можно определить величины изгибающих моментов и поперечных сил в любом сечении балки.

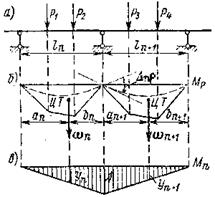
Рисунок 52 – Определение

побочного перемещения