Канонические уравнения метода перемещения

Развернем i-еуравнение системы (106), применяя принцип независимости действия сил:

R_i (Z₁, Z₂, Z_з, Р) = = 0.

Используя обозначения 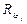= r_ij z_j , где r_ij - реакция i-й связи, вызванная единичным перемещением z_j j-й связи,получим i-е каноническое уравнение по МП при i = 1, 2, 3

r_i1 z₁+ r_i2 z₂ + r_i3 z₃ + R_iP = 0, (107)

где R_iP – реакция i-йсвязи от действия заданной внешней нагрузки.

Реакции r_ii называются собственными, а r_ij (i ≠ j) – побоч­ными. По теореме Релея о взаимности реакций имеем r_ij = r_ji (i ≠ j).

Таблица 2

Реакции и изгибающие моменты балок постоянного сечения

В общем случае при n дополнительных связях получим си­стему канонических уравнений в виде:

(108)

Коэффициенты r_ij и свободные члены R_iP канонических урав­нений могут быть найдены с помощью статического или общего способа, основанного на теореме о взаимности работ.

Рассмотрим применение статического способа, продолжив решение на примере рамы портала (см. рис. 56, а). В основе способа лежит использование уравнений статики: так как коэф­фициенты и свободные члены канонических уравнений являются реакциями связей основной системы, то их можно определить из уравнений равновесия. Реакция в виде момента определяется из условия равновесия вырезанного узла основной системы, реак­ция в виде силы – из уравнения равновесия какой-либо ее от­сеченной части.

На рис. 56, д-з построены единичные и грузовая эпюры. Направления определяемых перемещений и реакций те же, что и на рис. 56, г. Единичная эпюра М₁ при Z₁ = 1, Z₂ = Z₃ = 0 показана на рис. 56, д. Для построения ее использовано стандарт­ное решение (табл. 2): в частности, для первого стержня АВ, шарнирно опертого в узле А и защемленного в узле В,при единич­ном смещении заделки в узле В, и для второго стержня ВС, защем­ленного в узлах В и С, при единичном повороте заделки в узле В. При этом i = EJ/l – линейная жесткость балки. Реакция r₁₁ есть момент в узле В связи 1 при единичном перемещении Z₁= 1 этого же узла. На рис. 56, и показан вырезанный узел В основной системы с использованием эпюры М₁и данных табл. 2. Из урав­нения равновесия относительно центра узла В в виде ∑М = 0 имеем r₁₁ - 4i₂- 3i₁= 0, откуда r₁₁ = 4i₂+ 3i₁, где i₁ = E₁ J₁ / l₁, и т. д.

Реакция r₂₁ – момент в узле С (связи 2) при z₁= 1. Из равновесия узла С (см. рис.56, к)имеем r₂₁ – 2i₂ = 0, или r₂₁ = 2i₂.

Реакция r₃₁ – сила в связи 3 (см. рис. 56, д) при z₁= 1. Для ее определения вырежем второй стержень в основной системе при z₁=1 и рассмотрим его равновесие (см. рис.56, л).В силовой связи 3 действует реакция r₃₁, а в разрезанных стержнях 1 и 3 - поперечные силы Q_l и Q_з. Величина Q_l = 3i₁/l₁получена на основе стандартного решения табл. 2 первой балки при z₁= 1 (φ_А = 1).

Уравнение равновесия в виде ∑Х = 0 дает r₃₁ + Q_l + Qз = 0 и r₃₁ = - Q₁ = -3i₁/l₁.

Таким способом можно определить все реакции в наложенных связях при их единичных перемещениях. Остановимся для сравне­ния на реакции r₁₃ с использованием эпюры М₃. Для нахождения r₁₃ – реакции в первой связи при Z₃ = 1, Z₁ = Z₂ = 0 – следует рассмотреть равновесие узла В (табл.2) основной системы (рис.56, м)в виде r₁₃ + 3i₁ = 0, что дает r₁₃ = -3i₁/l₁. Как и cледовало ожидать, r₃₁ = r₁₃.

Определим, например, R_1P– реакцию в связи I (узел В) от действия внешней нагрузки. Вырежем узел В основной системы эпюры Мр (см. рис. 56, з) и. рассмотрим его равновесие (см. рис. 56, н)в виде ∑М = 0 (табл. 2):

R_1P + Gl₂/8 – ql₁²/8 = 0 и R_1P = - Gl₂/8 + ql₁²/8.

Аналогично определяются остальные реакции:

r₁₂ = r₂₁ = 2i₂; r₂₂ = 4i₂+ 3i₃; r_2З = r_З2 = - 3i₃/l₃;

r₃₃ = 3i₁/l₁+ 3i₃ /l₃; R_2P = - Gl₂/8; R_3P= -5ql₁/8.

Далее решается система канонических уравнений (108),записанная в виде трех уравнений, и определяются перемещения z₁ – z₃. Окончательная эпюра изгибающих моментов для заданной рамы (см. рис. 56, а) строится с использованием единичных эпюр М₁ - М_З и грузовой эпюры Мр как суммарная .

В приведенных на рис. 56 и 57 схемах металлических конструкций кранов число неизвестных по МП несколько превышает число неизвестных по МС. При малом числе неизвестных, когда расчет выполняется вручную, отдать предпочтение одному из методов можно только при рассмотрении конкретной задачи. В тех же случаях, когда число неизвестных значительно, расчет выполняется с применением ЭВМ (рис. 57). Метод перемещений более предпочтителен даже при k_H, несколько больших С_Н. Следует отметить, что МП усложняется, если расчет рам ведется с учетом деформации стержней от продольных и поперечных сил. В этом случае значение k_H увеличивается. При расчете ферм, стержни которых воспринимают продольные усилия, дополнительные связи по МП препятствуют деформации стержней. Для расчета рам иногда также применяют смешанный и комбини­рованный методы, которые сочетают одновременное использование МС и МП.

Литература: Основная: 6 [разд.7: стр. 57÷74].

Контрольные вопросы:

1. Какая балка называется неразрезной и каком случае она может быть статически неопределимой и зависимости от каких факторов определяется степень статической неопределимости неразрезной балки?

2. Как производится выбор основной системы для статически неопределимых систем и какой вид имеет уравнение в случае действия единичной силы Х_п?

3. Сколько неизвестных должно быть в каждом каноническом уравнении и напишите её и как определяются коэффициенты при неизвестных в каноническом уравнении?

4. Как определяется перемещение Δ_пр и напишите уравнение, а также уравнение трех моментов и дайте его определение?

5. Напишите зависимость для определения неизвестного усилия в ферме и по какой зависимости определяется окончательное усилие в любом стержне фермы?

6. Для составления системы канонических уравнений, какой теоремой следует пользоваться, и какую формулу необходимо применять, каким образом строятся линии влияния В, Q и М для один раз статически неопределимой балки, а также для опорных моментов у трехпролетной балки?