Расчеты на прочность при постоянных и переменных напряжениях по методам предельных состояний и допускаемых напряжений

Расчет металлических конструкций надлежит производить по методу предельных состояний или допускаемых. напряжений. В сложных случаях вопросы расчета конструкций и их элементов рекомендуется решать путем специально поставленных теорети­ческих и экспериментальных исследований. Прогрессивный метод расчета по предельным состояниям базируется на статистическом изучении действительной нагруженности конструкций в условиях эксплуатации, а также изменчивости механических свойств при­меняемых материалов. При отсутствии достаточно подробного статистического изучения действительной нагруженности кон­струкций тех или иных типов кранов расчеты их ведутся по ме­тоду допускаемых напряжений, базирующемуся на установлен­ных практикой коэффициентах запаса прочности. ­

При плоском напряженном состоянии в общем случае условию пластичности по современной энергетической теории прочности отвечает приведенное напряжение

, (169)

где σ_х и σ_у - напряжения по произвольным взаимно перпендикулярным осям координат х иу. При σ_у = 0

σ_пр = σ_Т, (170)

а если σ = 0, то предельные касательные напряжения

τ = = 0,578 σ_Т ≈ 0,6 σ_Т . (171)

Кроме расчетов на прочность для отдельных типов кранов существуют ограничения величин прогибов, которые имеют вид

f/l ≤ [f/l], (172)

где f/l и [f/l]- расчетное и допускаемое значения относительного статического прогиба f по отношению к пролету (вылету) l.Зна­чительные прогибы могут быть. безопасны для самой конструкции, но неприемлемы с эксплуатационной точки зрения.

Расчет по методу предельных состояний производится по нагрузкам, приведенным в табл. 3.

Примечания к таблице:

1. Комбинации нагрузок предусматривают следующую работу механизмов: . Iа и IIa – кран неподвижен; плавный (Ia) или резкий (IIа) подъем груза с земли или торможение его при опус­кании; Ib и IIb - кран в движении; плавный (Ib) и резкий (IIb) пуск или торможение одного из механизмов. В зависимости от типа крана возможны также комбинации нагрузок Ic и IIc и т. д.

2. В табл. 3 приведены нагрузки, постоянно действующие и регулярно возникающие при эксплуатации конструкций, образующие так называемые основные сочетания нагрузок.

Чтобы учесть меньшую вероятность совпадения расчетных нагрузок при более сложных их сочетаниях, вводятся коэффициенты сочета­ний n_с < 1, на которые умножаются коэффициенты перегрузок всех нагрузок, за исключением постоянной. Коэффициент соче­таний основных и дополнительных нерегулярно возникающих нагрузок, к которым относятся технологические, транспортные и монтажные нагрузки, а также нагрузки от температурных воз­действий, принимается равным 0,9; коэффициент сочетаний основ­ных, дополнительных и особых нагрузок (нагрузки от удара о бу­фера и сейсмические) – 0,8.

3. Для некоторых элементов конструкций следует учитывать суммарное воздействие как комбинации нагрузок Ia со своим коли­чеством циклов, так и комбинации нагрузок Ib со своим количе­ством циклов.

4. Угол отклонения груза от вертикали а. может также рас­сматриваться как результат косого подъема груза.

5. Давление ветра рабочего Р_{b II} и нерабочего - ураган­ного Р_{b III} - на конструкцию определяется по ГОСТ 1451-77. При комбинации нагрузок Ia и Ib давление ветра на конструкцию обычно не учитывается в силу малой повторяемости в год рас­четных скоростей ветра. Для высоких кранов, имеющих период свободных колебаний низшей частоты более 0,25 с и установлен­ных в ветровых районах IV-VIII по ГОСТ 1451-77, учитывается давление ветра на конструкцию при комбинации нагрузок Ia и Ib.

6. Технологические нагрузки могут относиться как к случаю нагрузок II, так и к случаю нагрузок III.

Таблица 3

Нагрузки при расчетах по методу предельных состояний

Предельными называются состояния, при которых конструкция перестает удовлетворять предъявляемым к ней эксплуатационным требованиям. Метод расчета по предельным состояниям имеет целью не допускать наступления предельных состояний при эксплуатации в течение всего срока службы конструкции.

Металлические конструкции ТТ (подъемно-транспортных машин) должны удовлетворять требованиям двух групп предельных со­стояний: 1) потеря несущей способности элементов крана по проч­ности или потеря устойчивости от однократного действия наиболь­ших нагрузок в рабочем или нерабочем состоянии. Рабочим счи­тается состояние, при котором кран выполняет свои функции (табл. 3, случай нагрузок II). Нерабочим считается состояние, когда кран без груза подвержен только нагрузкам от собствен­ного веса и ветра или находится в процессе монтажа, демонтажа и транспортировки (табл. 3, случай нагрузок III); потеря несущей способности элементов крана вследствие разру­шения от усталости при многократном действии нагрузок различной величины за расчетный срок службы (табл. 3, случай нагрузок I, а иногда и II); 2) непригодность к нормальной эксплуа­тации вследствие недопустимых упругих деформаций или коле­баний, которые влияют на работу крана и его элементов, а также обслуживающего персонала. Для второго предельного состояния по развитию чрезмерных деформаций (прогибов, углов поворота) предельное условие (172) устанавливается для отдельных типов кранов.

Наибольшее значение имеют расчеты по первому предельному состоянию, так как при рациональном проектировании конструк­ции должны удовлетворять требованиям второго предельного состояния.

Для первого предельного состояния по несущей способности (прочности или устойчивости элементов) предельное условие имеет вид

N ≤ Ф,(173)

где N - расчетная (наибольшая) нагрузка в рассматриваемом элементе, выраженная в силовых факторах (сила, момент, напря­жение); Ф - расчетная несущая способность (наименьшая) эле­мента соответственно силовым факторам.

При расчетах по первому предельному состоянию на проч­ность и устойчивость элементов для определения нагрузки N в формуле (171) так называемые нормативные нагрузки Р_Нi (для конструкций подъемно-транспортных машин это максималь­ные нагрузки рабочего состояния, вводимые в расчет как на ос­новании технических условий, так и на основании опыта проек­тирования и эксплуатации) умножаются на коэффициент пере­грузки соответствующей нормативной нагрузки n_i, после чего произведение Р_Hi п_i представляет собой наибольшую возможную за время эксплуатации конструкции нагрузку, называемую расчетной. Таким образом, расчетное усилие в элементе N в соответствии с расчетными сочетаниями нагрузок, приведенных в табл. 3, может быть представлено в виде

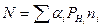, (174)

где α_i – усилие в элементе при Р_Нi = 1, а расчетный момент

, (175)

где М_Нi – момент от нормативной нагрузки.

Дляопределения коэффициентов перегрузки необходимо статистическое изучение изменчивости нагрузок по опытным данным. Пусть для данной нагрузки P_i известна ее кривая распределения (рис. 63). Поскольку кривая распределения всегда имеет асимптотическую часть, при назначении расчетной нагрузки над­лежит иметь в виду, что нагрузки, которые больше расчетных(на рис. 63 область этих нагрузок заштрихована), могут вы­звать повреждение элемента. Принятие больших значений для расчетной нагрузки и коэффициента перегрузки уменьшает ве­роятность повреждений и снижает убытки от поломок и аварий, но приводит к увеличению веса и стоимости конструкций. Вопрос о рациональном значении коэффициента перегрузки должен решаться с учетом экономических соображений и требований без­опасности. Пусть для рассматриваемого элемента известны кри­вые распределения расчетного усилия N и несущей способности Ф. Тогда (рис. 64) заштрихованная площадь, в границах которой нарушается предельное условие (173), будет характеризовать вероятность разрушения.

Приведенные в табл. 3 коэффициенты перегрузки n > 1, так как они учитывают возможность превышения действительными нагрузками их нормативных значений. В случае, если опасным является не превышение, а уменьшение действительной нагрузки по сравнению с нормативной (например, нагрузка на консоли балки, разгружающая пролетное строение, при расчетном сече­нии в пролете), коэффициент перегрузки для такой нагрузки следует принимать равным обратной величине, т. е. n' = 1/n < 1.

Для первого предельного состояния по потере несущей способности от усталости предельное условие имеет вид

σ_пр ≤ m_К R, (176)

где σ_пр – приведенное напряжение, а m_К – см. формулу (178).

Расчеты по второму предельному состоянию по условию (172) производятся при коэффициентах перегрузки, равных единице, т. е. по нормативным нагрузкам (вес груза принимается равным номинальному).

Функция Ф в формуле (173) может быть представлена в виде

Ф = Fm_КR , (177)

где F – геометрический фактор элемента (площадь, момент сопротивления и т. д.).

Под расчетным сопротивлением R следует понимать при расчетах:

на сопротивление усталости – предел выносливости элемента (с учетом числа циклов изменения нагрузки и коэффициентов концентрации и асимметрии цикла), умноженный на соответствую­щий коэффициент однородности по усталостным испытаниям, характеризующий разброс результатов испытаний, k₀ = 0,9, и деленный на k_м – коэффициент надежности по материалу при расчетах на прочность, характеризующий как возможность изме­нения механических качеств материала в сторону их снижения, так и возможность уменьшения площадей сечения проката из-за установленных стандартами минусовых допусков; в соответствую­щих случаях следует учесть снижение первоначального предела выносливости нагрузками второго расчетного случая;

на прочность при постоянных напряжениях R = R_п/k_м– ­частное от деления нормативного сопротивления (нормативного предела текучести) на соответствующий коэффициент надежности по материалу; для углеродистой стали k_м = 1,05, а для низколегированной – k_м = 1,1; таким образом, в отношении работы материала за предельное состояние принята не полная потеря его способности воспринимать нагрузку, а наступление больших пластических деформаций, препятствующих дальнейшему исполь­зованию конструкции;

на устойчивость -- произведение расчетного сопротивления на прочность на коэффициент уменьшения несущей способности сжимаемых (φ, φ_вн) или изгибаемых (φ_б) элементов.

Коэффициенты условий работы m_К зависят от обстоятельств работы элемента, которые не учитываются расчетом и качеством материала, т. е. не входят ни в усилие N, ни в расчетное сопро­тивление R.Таких основных обстоятельств три, и поэтому можно принять

m_K = m₁ m₂ m₃, (178)

где m₁– коэффициент, учитывающий ответственность рассчи­тываемого элемента, т. е. возможные последствия от разрушения; следует различать следующие случаи: разрушение не вызывает прекращения работы крана, вызывает остановку крана без повреж­дения или с повреждением других элементов и, наконец, вызы­вает разрушение крана; коэффициент m₁может находиться в пре­делах 1–0,75, в особых случаях (хрупкое разрушение) m₁ = 0,6; m₂– коэффициент, учитывающий возможные повреждения элементов конструкции в процессе эксплуатации, транспорти­ровки и монтажа, зависит от типов кранов; можно принимать т₂= 1,0÷0,8; т₃– коэффициент, учитывающий несовершенства расчета, связанные с неточным определением внешних сил или расчетных схем. Он должен устанавливаться для отдельных типов конструкций и их элементов. Можно принимать для плоских статически определимых систем т₃= 0,9, .а для статически неоп­ределимых –1, для пространственных –1,1. Для изгибаемых элементов по сравнению с испытывающими растяжение-сжатие т₃= 1,05. Таким образом, расчет по первому предельному состоянию на прочность при постоянных напряже­ниях производится по формуле

σ_II <. m_K R, (179)

а на сопротивление усталости, если переход к предельному со­стоянию осуществляется за счет увеличения уровня переменной напряженности, – по формуле (176), где расчетное сопротив­ление R определяется по одной из следующих формул:

R = k₀ σ_-1К /k_м ;(180)

R_N = k₀ σ_-1КN /k_м ; (181)

R* = k₀ σ_-1К /k_м ;(182)

R*_N = k₀ σ_-1КN /k_м ; (183)

где k₀, k_м- коэффициенты однородности по усталостным испы­таниям и надежности по материалу; σ_–1K, σ_–1KN , σ^*_–1K, σ^*_–1KN – пределы выносливости неограниченный, ограниченный, сниженный неограниченный, сниженный ограниченный соответственно.

Расчет по методу допускаемых напряжений производится по нагрузкам, приведенным в табл.4. Необходимо учитывать все примечания к табл. 3, кроме примечания 2.

Значения запасов прочности даны в табл. 5 и зависят от обстоятельств работы конструкции, не учитываемых расчетом, как например: ответственность, имея в виду последствия от разрушения; несовершенства расчета; отклонения в размерах и качестве материала.

Расчет по методу допускаемых напряжений производится в случаях отсутствия численных значений для коэффициентов перегрузки расчетных нагрузок для выполнения расчета по ме­тоду предельных состояний. Расчет на прочность производится по формулам:

σ_II ≤ [σ] = σ_T / n_II, (184)

σ_III ≤ [σ] = σ_T / n_III, (185)

где n_IIи n_III – см. в табл. 5. При этом допускаемые напря­жения на изгиб принимают на 10 МПа (примерно на 5 %) больше, чем на растяжение (для Ст3 180 МПа), учитывая, что при из­гибе текучесть сначала проявляет­ся только в крайних фибрах и рас­пространяется затем постепенно на все сечение элемента, повышая его несущую способность, т. е. при из­гибе имеет место перераспределение напряжений по сечению за счет пла­стических деформаций.

При расчете на сопротивление усталости, если переход к предель­ному состоянию осуществляется за счет увеличения уровня переменной напряженности, должно выполняться одно из следую­щих условий:

σ_пр ≤ [σ_–1K]; (186)

σ_пр ≤ [σ_–1KN]; (187)

σ_пр ≤ [σ^*_–1K]; (188)

σ_пр ≤ [σ^*_–1KN]; (189)

где σ_пр - приведенное напряжение; [σ_–1K], [σ_–1KN], [σ^*_–1K], [σ^*_–1KN] – допускаемые напряжения, при опреде­лении которых используется выражение [σ] = σ_–1K / n₁или аналогично формулам (181) – (183) вместо σ_–1Kиспользуются σ_–1KN , σ^*_–1K и σ^*_–1KN . Запас прочности n_Iтакой, как и при расчете статической прочности.

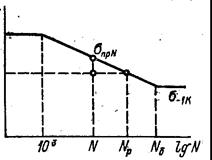
Рисунок 65 – Схема к расчету запаса по усталостной долговечности

Если переход к предельному состоянию осуществляется за счет увеличения числа циклов повторения переменных напряжений, то при расчете на ограниченную долговечность запас по усталост­ной долговечности (рис. 65) n_д = Np/ N. Так как σ^т_пр Np = σ^т_–1K N_б = σ^т_–1KN N,

n_д = (σ_–1KN / σ_пр)^т = п^т₁ (190)

и при n_l= 1,4 и К = 4 n_д ≈ 2,75, а при К = 2 n_д ≈ 7,55.

При сложном напряженном состоянии наиболее соответствует экспериментальным данным гипотеза наибольших касательных октаэдрических напряжений, в соответствии с которой

(191)

и . Тогда запас прочности при симметричных циклах

т. е. п = n_σn_τ / , (192)

где σ_-IK и τ_-lК - предельные напряжения (пределы выносливости), а σ_а и τ_a – амплитудные значения действующего симметричного цикла. Если циклы асимметричные, их следует привести к сим­метричным по формуле типа (168).

Прогрессивность .метода расчета по предельным состояниям заключается в том, что при расчетах по этому методу лучше учи­тывается действительная работа конструкций; коэффициенты перегрузки различны для каждой из нагрузок и определяются на основе статистического изучения изменчивости нагрузок. Кроме того, с помощью коэффициента надежности по материалу лучше учитываются механические качества материалов. В то время как при расчете по методу допускаемых напряжений надежность конструкции обеспечивается единым коэффициентом запаса, при расчете по методу предельных состояний вместо единого коэф­фициента запаса используется система трех коэффициентов: надежности по материалу, перегрузки и условий работы, уста­навливаемых на основании статистического учета условий работы конструкции.

Таким образом, расчет по допускаемым напряжениям есть частный случай расчета по первому предельному состоянию, когда коэффициенты перегрузки для всех нагрузок одинаковы. Однако надо подчеркнуть, что метод расчета по предельным состояниям понятия запаса прочности не использует. Его не использует также разрабатываемый в настоящее время для краностроения вероят­ностный метод расчета. Выполнив расчет по методу предельных состояний, можно определить значение получающегося при этом коэффициента запаса прочности по методу допускаемых напря­жений. Подставляя в формулу (173) значения N [см. фор­мулу (174)] и Ф [см. формулу (177)] и переходя к напряже­ниям, получим значение запаса прочности

п = Σσ_i n_i k_M / (m_KΣσ_i). (193)