Влияние концентраторов напряжений и асимметрии цикла нагружения на сопротивление усталости

Важнейшим параметром, по которому оценивается сопротивле­ние усталости, является эффективный коэффициент концентрации напряжений

К_σ=σ_-1 /σ_-1К, (151)

rде σ_-1 – предел выносливости при симметричном цикле гладкого образца, за который в металлических конструкциях принимается образец с сохраненной поверхностью проката без дополнительной концентрации напряжений; σ_-1К – то же для образца с концентрацией напряжений. В дальнейшем индекс σ у К опускаем.

Эффективный коэффициент концентрации меньше теоретиче­ского, так как в зоне концентратора имеются пластические де­формации и некоторое перераспределение напряжений. Так как у образцов сохраняется прокатная поверхность, в расчетах металлических конструкций не требуется подобно расчетам деталей машин учитывать отдельно качество поверхности. Значения К определяются экспериментально и для типовых элементов крано­вых металлических конструкций приведены в справочной литературе.

Для определения пределов выносливости по результатам испытаний партии одинаковых, насколько это достижимо, образ­цов строят кривые усталости. Каждый образец доводят до раз­рушения при циклической нагрузке с заданным коэффициентом асимметрии цикла R для всей партии. В результате статистической обработки полученных данных для отдельных точек усталостной кривой устанавливают число нагружений N_i, при котором раз­рушился образец с амплитудой напряжений σ_аi , т. е. его усталостную долговечность. Для элементов металлических конструкций кривые усталости наиболее близки к прямым в логарифмических координатах. Уравнение кривой усталости можно представить в виде σ ^т N = const, откуда σ ^т₁ N₁ = σ ^т₂ N₂; (σ₁ / σ₂) ^т = N₂/N₁;

т = (lg N₂ - ln N₁) / (lg σ_l - Ig σ₂) = ctg α. (152)

Пределу выносливости, являющемуся наибольшим напряжением, которое данный образец (элемент конструкции) выдерживает в те­чение сколь угодно большого числа циклов, можно дать определе­ние как напряжению, соответствующему горизонтальному участку на кривой усталости (рис. 58, линия ОВ).Экспериментально установлено, что при значениях К < 2 предел выносливости достигается при числе циклов переменных напряжений N_б = 2·10⁶, при К ≥ 2 предел выносливости достигается при N_б = 5·10⁶, причем закон изменения кривой усталости на участке от 2·10⁶ до 5·10⁶ сохраняется прежним, а испытания на базе N_б = 10·10⁶ никаких уточнений в значения пределов выносливо­сти не вносят. Если при напряже­ниях σ > σ_RK элемент выдерживает число циклов N < N_б то значение σ_RKN (рис.58) назы­вается пределом ограниченной вы­носливости при числе циклов N. Кривые усталости для основного металла и для образцов с различными концентраторами из углеро­дистых и низколегированных сталей, хорошо изученные в диа­пазоне чисел циклов N от 10⁵ до 2·10⁶, сохраняют свою зако­номерность и на некотором участке при N < 10⁵, приблизи­тельно до 10³ циклов при σ ≈ 0,8σ_в. Для значений N < 10³ – области квазистатических разрушений, сопровождаю­щихся образованием шейки, кривая усталости становится более пологой и приходит в точку, соответствующую разрыву при

статическом нагружении.

 

 

Так как пределы выносливости определяются эксперимен­тально, то естественно, что путем испытаний установить их при всех значениях R и К невозможно. Эксперименты показывают, что если результаты испытаний по определению пределов вы­носливости изобразить в виде диаграммы, на которой по оси орди­нат откладывать значения σ_max и – σ_min а по оси абсцисс­ – значения среднего напряжения σ_m (рис. 59), то такая диаграмма может быть образована из прямых линий. Таким образом, для построения диаграммы нужны лишь две экспериментальные точки, по данным усталостных испытаний. Одной из них обычно бывает точка, соответствующая симметричному циклу А - А', а дру­гой - какая-либо точка, например соответствующая отнулевому циклу В - В';Наибольшее расчетное значение предела вы­носливости не должно превышать предельных значений стати­ческой прочности (для металлических конструкций предела теку­чести σ_т), и поэтому верхняя и нижняя части диаграммы ограни­чиваются значениями σ_т, Таким образом, если напряженное состояние элемента характеризуется значениями σ_max и σ_m, лежащими на контурной линии диаграммы (рис. 59), то оно соответствует пределу выносливости, если внутри контурной линии диаграммы, то имеется запас по отношению к пределу выносливости, а если вне контурной линии, то это соответствует пределу ограниченной выносливости при числе циклов, меньшем N_б (см. рис. 58). Так как

tg β = σ_RK / σ_m= σ_max / σ_m = 2 σ_max /( σ_max + σ_min) = 2/(1 + R),

то каждому лучу, проведенному из начала координат, соответ­ствует определенное значение R. Так, для оси ординат при R = –1 tg β = ∞, для отнулевого цикла при R = 0 tg β = 2, а угол β, при котором луч проходит через точку Е (рис. 59),определяет предельное значение R для расчетов на выносливость.

Определим аналитическое выражение предела выносливости σ_RK для заданных значений R и К. Из экспериментальных дан­ных можно считать. что К ≈ σ_а/σ_ак не зависит от величины среднего напряжения σ_m,т. е. эффект концентрации напряже­ний относится лишь к амплитуде цикла. Тогда для точки М на рис. 60, являющемся частью диаграммы, подобной диаграмме на рис. 59:

σ_max = σ_RK = σ_аК + σ_m = σ_а/К + σ_m; (153)

σ_а + σ_m = σ_–l + σ_mtg γ = σ_–l + (σ₀ – σ_–l) σ_m /(0,5 σ₀);

 

σ_а = σ_–l – σ_m(1 – tg γ) = σ_–l – ψ_σ σ_m, (154)

где

ψ_σ = (2 σ_–l – σ₀)/ σ₀. (155)

Коэффициент ψ_σ характеризует наклон линии предельных напря­жений и называется коэффициентом чувствительности металла к асимметрии цикла напряжений. В дальнейшем индекс σ у ψ опускаем. Так как

σ_m= 0,5 (σ_max + σ_min) = 0,5 (1 + R) σ_max = 0,5 (1 + R) σ_RK, (156)

то, подставляя в уравнение (153) значения σ_а и σ_m[см. формулы (154) и (156)], получим

σ_RK = . (157)

Для σ_max > 0 это уравнение справедливо как в области σ_m > 0, так и в области σ_m < 0, т. е. для циклов, приведенных на рис. 57, д, и соответствует σ_RK при N_б = 2·10⁶, так как при этом числе циклов определяется σ_–l. Для σ_m< 0, поскольку |σ_min| > σ_max и σ_RK = σ_min, для цикла с коэффициентом асимметрии R (см. рис. 59)

tgβ = ­ σ_RK / σ_m = σ_min / σ_m = R σ_max / σ_m = 2R / (1 + R),

где

. (158)

Рисунок 60 – Схема к определению предела выносливости ­ σ_RK

Это значит, что лучу, проведенному из начала координат к линии предельных циклов (проходящему через точки А и В) и имеющему в области σ_m > 0 коэффициент асимметрии R, в об­ласти σ_m < 0 соответствует цикл со значением 1/R (см. рис. 59). Таким образом, пределы выносливости для σ_m > 0 обозначаются на линии АЕ, а для σ_m < 0 – на линии A'F'.B области σ_m < 0рассматриваемая схематизированная диаграмма не является симметричной по отношению к области σ_m > 0. Размах колебаний напряжений σ_max –|σ_min|| по мере уменьшения σ_mнепрерывно растет. Например, предел выносливости при отнулевом цикле растяжения (R = 0) из уравнения (157) ­ σ_RK = 2 σ_–l /(К + ψ), а при отнулевом цикле сжатия из уравнения (158) при R = – ∞ σ_RK = – 2 σ_–l /(К – ψ), т. е. больше, чем при R = 0, по абсо­лютному значению в 1,5 -1,1 раза в зависимости от значений К. По данным пульсаторных испытаний, для образцов с сохраненной поверхностью проката из углеродистых и некоторых низколеги­рованных сталей σ_–l ≈ 0,35σ_В и ψ = 0,2. Так как кривая уста­лости на участке от 2·10⁶ до 5·10⁶ сохраняет свою закономер­ность, значение . σ_RK, полученное при N_б = 2·10⁶, умножается на для получения значения σ_RK при N_б = 5·10⁶ циклов.

Из анализа результатов испытаний есть основание считать, что существует связь между наклоном усталостной кривой и значе­нием эффективного коэффициента концентрации. В первом при­ближении для металлических конструкций как из углеродистых, так и из низколегированных сталей, для которых σ_–l ≈ 0,35 σ_В, для ориентировочной оценки можно принимать

тК ≈ const ≈ 12. (159)

Если расчет ведется на ограниченный срок службы, то из уравнения усталостной кривой σ^т N = const предел ограниченной выносливости

 

. (160)

Эффективный коэффициент концентрации напряжений К в за­висимости от конструкции соединения принимается по справоч­ным данным. Для листовых сварных и клепаных конструкций К < 2,0÷2,5, для сварных решетчатых конструкций К =2÷4. Конструкции соединений, дающие значения К > 4, следует признать недопустимыми. Во всех случаях для конструк­ций из низколегированных сталей, обладающих большими зна­чениями σ_В и меньшими значениями относительного удлинения, значения К в 1,1-1,4 раза больше, чем для конструкций из угле­родистых сталей, что снижает эффективность применения низко­легированных сталей в конструкциях, рассчитываемых на сопро­тивление усталости. При этом в ряде случаев целесообразно, применяя низколегированные стали, с помощью конструктивных и технологических мероприятий добиваться снижения значе­ний К.

Экспериментальный способ определения пределов выносли­вости элементов металлических конструкций путем усталостных испытаний сварных образцов, естественно, не может установить усталостные характеристики для всего многообразия встреча­ющихся в практике случаев конструктивного исполнения соеди­нений и узлов. Поэтому есть предложения по теоретическому определению пределов выносливости сварных соединений. Эти предложения базируются на дифференцированном и количествен­ном учете таких факторов, как концентрация напряжений, меха­нические свойства металла расчетной зоны (измененные перво­начальные механические свойства в результате термического и механического воздействия), остаточные напряжения, геометри­ческие размеры соединений, начальные нерасчетные несовершен­ства конструкций (местный изгиб) и вид напряженного состояния.

Расчетное определение пределов выносливости позволяет на стадии проектирования оценивать влияние основных конструк­тивных и технологических факторов на сопротивление усталости.

Литература:

Основная: 6 [разд. 12: с.120÷127, 136 – 137]; 1 [разд. 3, стр. 126].

Контрольные вопросы.

1. Назовите основные расчетные случаи сочетания нагрузок рекомендуемые для ТТ, каким условиям они соответствуют и как по ним производится расчет, а также методы расчета металлических конструкций ТТ, какой из них является наиболее распространенным?

2. Какой метод расчета металлических конструкций ТТ является прогрессивным и на чем он базируется, а также на чем базируется расчет металлических конструкций ТТ по методу допускаемых нагрузок?

3. В чем заключается сущность особенности работы металлических конструкций ТТ при переменных напряжениях, сколько и какие виды излома существуют в металлических конструкциях ТТ, приведите ихние характеристики?

4. Вследствие чего получаются преждевременные усталостные разрушения в металлических конструкциях ТТ и как определяется характер цикла переменных напряжений и какие различные виды циклов переменных напряжений существуют?

5. По какому важнейшему параметру оценивается сопротивление усталости и дайте его характеристику, напишите уравнение кривой усталости для элементов металлических конструкций ТТ?

6. Как производится определение аналитического выражения предела выносливости элементов металлических конструкций ТТ?

 

Тема лекции: Основные положения расчета металлоконструкций при переменных напряжениях. Расчеты на прочность при постоянных и переменных напряжениях по методам предельных состояний и допускаемых напряжений.

Расчет элемента металлической конструкции может быть выполнен наиболее точно, если для него за весь срок службы ТТ экспериментально установлены законы изменения дей­ствующих эксплуатационных напряжений (нагрузок) σ_min и σ_max и корреляционные связи между ними. Однако такими дан­ными в достаточном количестве краностроение пока не распо­лагает и получение таких данных для отдельных групп кранов сопряжено с большими затратами труда и времени. Поэтому впредь до накопления необходимых статистических данных о фактической суммарной нагруженности рассчитываемых элементов конструк­ций следует пользоваться расчетными сочетаниями нагрузок, устанавливаемыми на основании опыта эксплуатации отдельных групп кранов.

При этом изучается изменчивость отдельных со­ставляющих общей нагруженности с учетом частоты их .повто­рения, что значительно менее трудоемко по сравнению с изучениемдействительной суммарной нагруженности рассчитываемых элементов. Отдельные составляющие общей нагруженности пред­ставляются в виде или кривых распределения, или эксперимен­тальных кривых, или гистограмм, а при отсутствии таких данных могут приниматься по типовым графикам нагрузки (рис. 61, а), которые составлены в зависимости от режима работы крана: 1 – весьма тяжелый; 2 – тяжелый и 3 – средний. Для кранов легкого режима работы влияние действия переменности напря­жений не учитывается. Здесь P_i /P_н– относительное значение i-гоуровня нагрузки в долях от номинальной нагрузки; Z_i / Σ Z_i – относительное число повторений нагрузки на i-м уровне в долях от полного числа повторений Σ Z_i ≤ N_б данной нагрузки за срок службы крана.

Рисунок 62 – К определению приведенных напряжений

Рисунок 61 – Типовые графики нагрузки

 

Достоинством способа установления закономерностей внеш­него нагружения для отдельных видов нагрузок является то, что такие данные могут быть достаточно точно использованы вне зависимости от конструктивного исполнения кранов данного типа, а также для прогнозирования нагружения кранов этого типа, но других параметров. В качестве примера можно указать на достаточно широкие возможности использования типовых гра­фиков нагрузки (рис. 61, а).К недостаткам этого способа отно­сится необходимость выявления расчетных сочетаний отдельных нагрузок.

Приведение действующих нестационарных напряжений к ста­ционарным производится на основе закона суммирования уста­лостных повреждений. Под приведенным напряжением σ_пр под­разумевается напряжение с такой амплитудой стационарного режима, действие которого по эффекту накопления повреждения эквивалентно данному нестационарному режиму. Введение в рас­чет приведенных напряжений способствует уменьшению метал­лоемкости конструкций, поскольку σ_пр < σ_max.Условие сум­мирования повреждаемости дает разрушение, а для усло­вий прочности оно имеет вид , или . Так как , то < ,

откуда σ_RK > .

Тогда

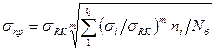(161)

и коэффициент режима работы

. (162)

Запас прочности по выносливости

n = σ_RK / σ_пр. (163)

Таким образом, расчет при нестационарном режиме приводится к форме, аналогичной расчету при стационарном режиме напря­женного состояния. Приведенное напряжение можно определить также для числа циклов N = Σ n_i < N_б.Тогда

σ_{пр N} = σ_RK (164)

и аналогично уравнению (160) σ_{пр N} = σ_пр . (165)

Отношения σ_RK / σ_при σ_RKN / σ_прN характеризуют значения запасов (рис. 62). Так как для напряженного состояния при растяжении, сжатии и изгибе напряжения пропорциональны нагрузкам, то аналогично формуле (164) находим эквивалентную нагрузку

, (166)

где Р_Н – номинальная, т. е. полная для расчета на проч­ность, нагрузка; ΣZi ≤ N_б – суммарное количество нагружений за срок службы крана; т - значения, устанавливаемые по справочным данным; φ_э – коэффициент режима нагрузки, равный

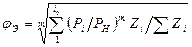. (167)

Как видно, φ_э отражает относитель­ное количество циклов нагружения Z_i / ΣZi за срок службы крана и от­носительную их величину P_i /P_н что связано с режимом работы.

Если для рассчитываемого крана отсутствуют данные о закономерно­сти его внешнего нагружения от отдельных видов нагрузок, следует использовать типовые графики нагрузок, которые, например, при четырехступенчатой гистограмме(см. рис. 61, 6) и при т = 4, для тяжелого режима работы дают значение

φ_э = = 0,82,

то же при двухступенчатой гистограмме (см. рис. 61, в)

φ_э = = 0,77.

Практически можно принимать для весьма тяжелого режима нагрузки φ_э = 1, для тяжелого – φ_э = 0,8÷0,7, для среднего – φ_э = 0,7÷0,6 (большие значения при К < 2; меньшие – при К = 4).

От эквивалентного значения. Р_Э каждой нагрузки в рассчи­тываемом сечении определяется эквивалентное напряжение .Для того чтобы сделать возможным последующее суммирование по сочетаниям нагрузок, эти напряжения , имеющие свои коэффициенты асимметрии расчетного цикла Ri и эффективный коэффициент концентрации К, приводятся к напряжениям сим­метричного цикла из условия сохранения одинакового запаса по пределам выносливости по формуле

. (168)

При этом коэффициент асимметрии цикла Ri в значении предела выносливости не во всех случаях будет совпадать с коэф­фициентом асимметрии расчетного цикла напряжений .