Плотность квантовых состояний

Наиболее важной характеристикой электронного энергетического спектра является распределение электронных состояний по энергиям. Количественно описать это распределение можно, используя понятие "плотность состояний".

Пусть в кристалле единичного объема в интервале энергий от Е до Е+dE имеется dN квантовых состояний (безучета спина). В выбранном интервале энергии dE=const при различных значениях величины энергии Е число состояний dN может различаться. Поэтому будем считать, что

во-первых, dN зависит от величины Е, то есть dN = dZ (Е);

во-вторых, связь между dN и dE задается соотношением

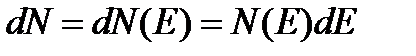, (2.1)

где коэффициентN, называемый плотностью состояний,также зависит от величины Е. Физический смысл плотности состояний очевиден. Из соотношения (2.1) следует:

N(E)= , (2.2)

следовательно, плотность состояний – это число состояний в единичном интервале энергий для единичного объема кристалла.

Точный расчет величины N(Е) является сложной квантовомеханической задачей, так как ее значениетесным образом связано с фор­мой изоэнергетических поверхностей. Действительно, построим в зоне Бриллюэна две изоэнергетические поверхности Е и Е+dE. Они выделяют некоторый тонкий слой (величина dp очень мала) в пространстве квазиимпульса (рис. 2.1). Пусть объем этого слоя составляет dГ, а объем одного квантового состояния в фазовом пространстве – γ. Тогда количество состояний в выделенном слое составит:

(2.3)

Определим объем квантового состояния в фазовом пространстве γ. Состояние электрона можно отождествить с тем объемом, который приходится на электрон при его изображении в фазовом пространстве. По принципу неопределенности Гейзенберга, одновременное определение координаты и импульса частицы возможно лишь с точностью, не лучше постоянной Планка - 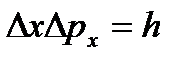. В применении к трехмерному пространству это означает, что электрон как бы размазан в фазовом пространстве координат и импульсов по каждой из его координат на величину h. Поэтому фазовый объем такого электрона:

(2.4)

Т.е. под состоянием электрона можно понимать минимальный фазовый объем равный h³. Следовательно, задача определения N(E) сводится к нахождению количества элементарных объемов h³, соответствующих энергетическому интервалу dE:

N(E)= = 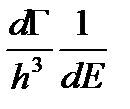(2.5)

Входящую в выражение (2.5) величину объема слоя в пространстве квазимпульса dГ можно найти, если известно уравнение изоэнергетической поверхности.

Рассмотрим некоторые частные случаи.

1. Предположим, что изоэнергетические поверхности имеют форму сферы с минимальной энергией E_min в центре зоны Бриллюэна (рис.2.2). Этот случай характерен для зоны проводимости некоторых прямозонных полупроводников, таких, например, как GaAs (см. рис. 1.54). Пусть

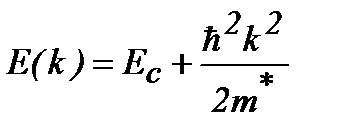или (2.6)

Две изоэнергетические поверхности Е и Е+dЕ выделяют сферический слой толщиной dp и объемом dГ(Е, Е+dE) (рис. 2.2):

Рис. 2.2. Объем сферического слоя в зоне Бриллюэна, заключенного между двумя изоэнергетическими поверхностями Е и Е+dE.

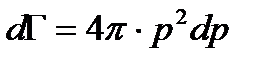(2.7)

Воспользовавшись соотношением (2.6), выразим p через E :

(2.8)

Дифференцируя по k первое выражение в (2.8), получим

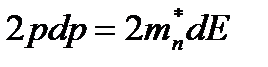(2.9)

Учитывая соотношения (2.7), (2.8) и (2.9), можем записать:

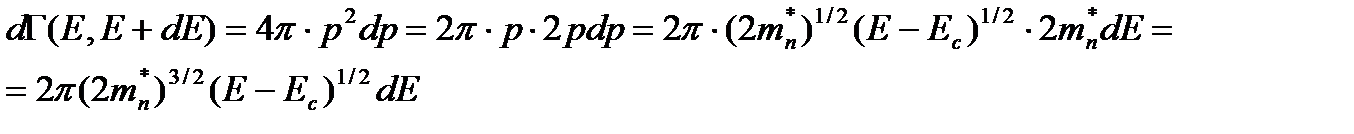(2.10)

Для dN из (2.5) и (2.10) получим

(2.11)

Или учитывая две ориентации спина:

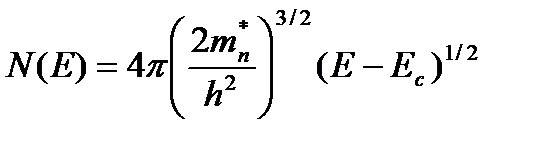(2.12)

Таким образом, если энергия носителей заряда является квадратичной функцией квазимпульса, то плотность состояний N(Е) имеет зависимость от энергии вида .

2. Рассмотрим теперь случай, когда изоэнергетические поверхности также являются сферами, однако минимум энергии находится не в центре зоны Бриллю­эна, а в некоторых точках р₀, причем число минимумов равно М (рис. 2.3) .

Построив изоэнергети­ческие поверхности Е, Е+dE, мы получим М сфер. Уравнение одной из них имеет вид

. (2.13)

Рис. 2.3. Случай М сферических поверхностей, расположенных на расстоянии p0 от центра зоны Брюллеэна.

Радиусы сфер |p-p₀|, толщина сферического слоя d|p-p₀|; но число сфер равно теперь М, поэтому интервалу энергии dE со­ответствует суммарный объем М слоев:

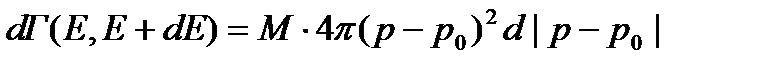(2.14)

Выражая |p-p₀| и d|p-p₀| через энергию, получим для плотности квантовых состояний (с учетом двух ориентаций спина) формулу, аналогичную (2.12):

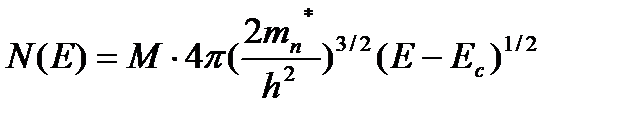(2.15)